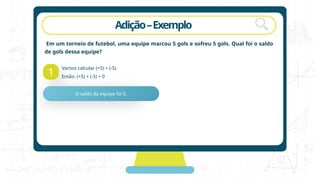
O documento aborda operações com números inteiros, incluindo adição, subtração, multiplicação e divisão, além das propriedades associativas, comutativas e distributivas. Exemplos práticos são apresentados para ajudar na compreensão das operações, como a soma de pontos em torneios e a soma algébrica. A importância da ordem das operações e do tratamento de parênteses também é enfatizada ao longo do texto.

1. Operaçõescom
Números Inteiros
Nome do Prof

2. Adição–Exemplo1
Ao disputar um torneio de handebol, a equipe da Escola do Bairro obteve 4 pontos no
primeiro turno e 5 pontos no segundo turno. Quantos pontos a equipe obteve ao todo
nesse torneio?
1
Nessa situação, devemos calcular (+4) + (+5).
Então: (+4) + (+5) = +9
A equipe obteve ao todo 9 pontos

3. Adição–Exemplo2
Nesse mesmo torneio, a equipe da Escola Fundamental perdeu 2 pontos no primeiro
turno e 4 pontos no segundo turno. Quantos pontos a equipe perdeu ao todo nesse
torneio?
1
Vamos calcular (-2) + (-4).
Então: (-2) + (-4) = -6
Essa equipe perdeu ao todo 6 pontos

4. Adição–Exemplo3
Jonas entrou no elevador no andar térreo. Desceu, inicialmente, 2 andares e, em
seguida, subiu 6 andares. Em qual andar o elevador parou?
1
Vamos calcular (-2) + (+6).
Então: (-2) + (+6) = +4
O elevador parou no 4º andar.

5. Quando adicionamos números
inteiros commesmo sinal, a soma
é obtida adicionando seus
módulos e mantendo osinal.

6. Adição–Exemplo
Jonas entrou no elevador no andar térreo. Desceu, inicialmente, 2 andares e, em
seguida, subiu 6 andares. Em qual andar o elevador parou?
1
Vamos calcular (-2) + (+6).
Então: (-2) + (+6) = +4
O elevador parou no 4º andar.

7. Quandoadicionamosdoisnúmeros
inteirosdesinaisdiferentes,asomaé
obtidaefetuando-sea diferençaentreseus
módulosemantendoosinaldonúmero
queestámaisdistantedaorigem

8. Propriedades da adição
1
A soma de dois números inteiros é sempre
um número inteiro
(+3) + (+5) = +8, e +8 (dizemos que +8
pertence ao conjunto dos inteiros).
(-7) + (-3) = -10, e -10 .
(+11) + (-8) = +3, e +3 .
(+7) + (-13) = -6, e -6 .

9. Propriedades da adição
2
A ordem das parcelas em uma adição não altera
a soma. Essa é a propriedade comutativa
(+11) + (-9) = +2
ou
(-9) + (+11) = +2
(+11) + (-9) = (-9) + (+11)

10. Propriedades da adição
3
Associando-se as parcelas de maneiras
diferentes, obtém-se a mesma soma. Essa é
a propriedade associativa.
(-8) + (-2) + (+7) = (-10) + (+7) = -3
(-8) + (-2) + (+7) = (-8) + (+5) = -3

11. Propriedades da adição
4
O número 0 é o elemento neutro da adição
em ℤ. Essa é a propriedade da existência do
elemento neutro.
(+8) + 0 = 0 + (+8) = +8
(-7) + 0 = 0 + (-7) = -7

12. Além dessas propriedades da adição, que
também são válidas para o conjunto ℕ, o
conjunto ℤ apresenta uma nova propriedade:
existência do elemento oposto
Propriedades
da adição
(-8) + (+8) = 0 -8 é o elemento oposto ou
→
simétrico de +8 e vice-versa
(+13) + (-13) = 0 +13 é o elemento oposto ou
→
simétrico de -13 e vice-versa.
A soma de dois números
opostos é igual a 0 (zero)

13. Adição–Exemplo
Em um torneio de futebol, uma equipe marcou 5 gols e sofreu 5 gols. Qual foi o saldo
de gols dessa equipe?
1
Vamos calcular (+5) + (-5).
Então: (+5) + (-5) = 0
O saldo da equipe foi 0.

14. Subtrair dois números
inteiros é o mesmo que
adicionar o primeiro com o
oposto do segundo

15. Como toda subtração em ℤ pode ser transformada em
adição, dizemos que a adição e a subtração de
números inteiros podem ser consideradas uma única
operação, chamada adição algébrica, cujo resultado é
denominado soma algébrica
Adição Algébrica
Toda expressão numérica que contém
somente as operações de adição, ou
subtração, ou ambas, representa uma adição
algébrica

16. Quando uma adição algébrica contém parênteses
precedidos do sinal +, podemos eliminar esses
parênteses, bem como o sinal que os precede,
escrevendo cada número que está no interior dos
parênteses com o seu próprio sinal
Adição Algébrica
10 + (-6) = 10 - 6 = 4
-7 + (-5 + 4) = -7 -5 + 4 = -12 + 4 = -8

17. Quando uma adição algébrica contém parênteses
precedidos do sinal -, podemos eliminar esses
parênteses, bem como o sinal que os precede,
escrevendo cada número que está no interior dos
parênteses com o sinal trocado
Adição Algébrica
10 - (-6) = 10 + (+6) = 10 + 6 = 16
-7 - (-5 + 4) = -7 + (+5 - 4)
= -7 + 5 - 4 = 5 - 11 = -6
As mesmas regras valem para as adições
algébricas em que aparecem colchetes e
chaves, além dos parênteses

18. Exemplos
Calcular a soma algébrica 20 + (-9 + 12) - (-15 + 20).
1
Vamos fazer esse cálculo de dois modos diferentes

19. Exemplos
Calcular a soma algébrica 20 + (-9 + 12) - (-15 + 20).
2
Vamos fazer esse cálculo de dois modos diferentes

20. A multiplicação de dois
números inteiros positivos
dá um número inteiro
positivo

21. Multiplicação–Exemplo
Os dois fatores são números inteiros positivos. Considerando a multiplicação dos
números naturais, temos:

22. Multiplicação–Exemplo
1
Os dois fatores são números inteiros negativos.
Consideremos o quadro de multiplicação:
x -4 -3 -2 -1 0 +1 +2
-6 ? ? ? ? ? ? ?
Sabemos que: (-6) x 0 = 0 (-6) x (+1) = -1 (-6) x (+2) = -12

23. Multiplicação–Exemplo
x -4 -3 -2 -1 0 +1 +2
-6 ? ? ? ? 0 -6 -12
2
Observando a linha dos resultados, notamos que cada resultado à sua esquerda tem 6 unidades
a mais que o resultado anterior. Mantendo esse padrão, preenchemos o restante do quadro:
x -4 -3 -2 -1 0 +1 +2
-6 +24 +18 +12 +6 0 -6 -12

24. Propriedades da multiplicação
1
O produto de dois números inteiros é
sempre um número inteiro
(+7) x (+9) = +63, e +63 ℤ.
∈
0 x (-41) = 0, e 0 ℤ.
∈
(-2) x (+16) = -32, e -32 ℤ.
∈
(-7) x (-11) = +77, e +77 ℤ.
∈

25. Propriedades da multiplicação
2
A ordem dos fatores não altera o produto. Essa é
a propriedade comutativa
(-9) x (+12) = -108
ou
(+12) x (-9) = -108
(-9) x (+12) = (+12) x (-9)

26. Propriedades da multiplicação
3
Associando-se os fatores de maneiras
diferentes, obtém-se o mesmo produto. Essa
é a propriedade associativa.
(-10) x (+8) x (+5) = (-80) x (+5) = -400
(-10) x (+8) x (+5) = (-10) x (+40) = -400

27. Propriedades da multiplicação
4
O número +1 é o elemento neutro da
multiplicação de números inteiros. Essa é a
propriedade da existência do elemento neutro.
(+8) x (+1) = (+1) x (+8) = +8
(-10) x (+1) = (+1) x (-10) = -10

28. Propriedades da multiplicação
5
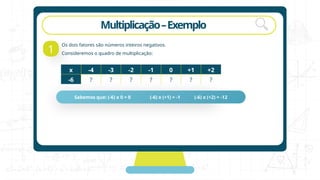
Para multiplicar um número inteiro por uma soma algébrica,
podemos multiplicar cada parcela pelo número e adicionar, a seguir,
os resultados obtidos. Essa é a propriedade distributiva em relação à
adição algébrica.
(+6) x [(+3) + (-5)] = (+6) x (+3) + (+6) x (-5) = (+18) + (-30) = 18 - 30 = -12
(-9) x (-3 + 7) = (-9) x (-3) + (-9) x (+7) = (+27) + (-63) = +27 - 63 = -36

29. Quando efetuamos uma divisão exata entre dois
números inteiros não nulos, o quociente será um
número inteiro positivo se o dividendo e o divisor
tiverem mesmo sinal
Caso contrário, o quociente será um número inteiro
negativo
Divisão exata de
números inteiros

30. Potenciação de Números Inteiros
1
Quando o expoente for um número par, a potência será
sempre um número inteiro positivo

31. Potenciação de Números Inteiros
2
Quando o expoente for um número ímpar, a potência terá
sempre o mesmo sinal de base

32. Raiz quadrada exata de um número inteiro positivo
é um número inteiro positivo que, elevado ao
quadrado, resulta no número inicial
Raiz Quadrada
Exata de Números
Inteiros
A raiz quadrada de 16 é o número
positivo +4
Indica-se:

33. Observe que, nas expressões numéricas com
números inteiros, também seguimos a mesma ordem
das operações válidas para as expressões com
números naturais
1
2
Em seguida, as divisões e as multiplicações, na ordem em que
aparecem
3
em seguida, as divisões e as multiplicações, na ordem em que
aparecem
4
Devemos respeitar a eliminação dos sinais de associação
(parênteses, colchetes e chaves).
Primeiro resolvemos as raízes quadradas e as potenciações, na
ordem em que aparecem

34. Expressões Numéricas