Lista 02 exercícios de função do 1º grau (gabarito)
•
2 gostaram•43,551 visualizações
Denunciar
Compartilhar
Denunciar
Compartilhar
Baixar para ler offline
Recomendados
Recomendados
Mais conteúdo relacionado
Mais procurados
Mais procurados (20)
Expressões algébricas e valor numérico de expressões algébricas

Expressões algébricas e valor numérico de expressões algébricas
Listão 9º ano - Função de 1º e 2º grau e Probabilidade

Listão 9º ano - Função de 1º e 2º grau e Probabilidade
9 º ano função de 1º grau e teorema de tales exercícios

9 º ano função de 1º grau e teorema de tales exercícios
Destaque
Destaque (14)
Mat utfrs 10. produtos notaveis e fatoracao exercicios

Mat utfrs 10. produtos notaveis e fatoracao exercicios
1ª lista de exercícios 9º ano(potências)ilton bruno

1ª lista de exercícios 9º ano(potências)ilton bruno
Mat utfrs 12. equacoes do 1° e 2° graus exercicios

Mat utfrs 12. equacoes do 1° e 2° graus exercicios
Lista de exercícios 8º ano - 3ª etapa - produto notável

Lista de exercícios 8º ano - 3ª etapa - produto notável
Semelhante a Lista 02 exercícios de função do 1º grau (gabarito)
Semelhante a Lista 02 exercícios de função do 1º grau (gabarito) (20)
Aula de Apresentação, Função e Função do 1º Grau.ppt · versão 1.pptx

Aula de Apresentação, Função e Função do 1º Grau.ppt · versão 1.pptx
Lista de exerc_funçao_afim_prova_auxiliar_1_ano_2012_pdf

Lista de exerc_funçao_afim_prova_auxiliar_1_ano_2012_pdf
Último
Slides Lição 5, Betel, Ordenança para uma vida de vigilância e oração, 2Tr24....

Slides Lição 5, Betel, Ordenança para uma vida de vigilância e oração, 2Tr24....LuizHenriquedeAlmeid6
Último (20)
Revolução russa e mexicana. Slides explicativos e atividades

Revolução russa e mexicana. Slides explicativos e atividades
Considere a seguinte situação fictícia: Durante uma reunião de equipe em uma...

Considere a seguinte situação fictícia: Durante uma reunião de equipe em uma...
Projeto de Extensão - ENGENHARIA DE SOFTWARE - BACHARELADO.pdf

Projeto de Extensão - ENGENHARIA DE SOFTWARE - BACHARELADO.pdf
Reta Final - CNU - Gestão Governamental - Prof. Stefan Fantini.pdf

Reta Final - CNU - Gestão Governamental - Prof. Stefan Fantini.pdf
planejamento_estrategico_-_gestao_2021-2024_16015654.pdf

planejamento_estrategico_-_gestao_2021-2024_16015654.pdf
Slides Lição 5, Betel, Ordenança para uma vida de vigilância e oração, 2Tr24....

Slides Lição 5, Betel, Ordenança para uma vida de vigilância e oração, 2Tr24....
PROGRAMA DE AÇÃO 2024 - MARIANA DA SILVA MORAES.pdf

PROGRAMA DE AÇÃO 2024 - MARIANA DA SILVA MORAES.pdf
DeClara n.º 75 Abril 2024 - O Jornal digital do Agrupamento de Escolas Clara ...

DeClara n.º 75 Abril 2024 - O Jornal digital do Agrupamento de Escolas Clara ...
PROJETO DE EXTENSÃO - EDUCAÇÃO FÍSICA BACHARELADO.pdf

PROJETO DE EXTENSÃO - EDUCAÇÃO FÍSICA BACHARELADO.pdf
5 bloco 7 ano - Ensino Relogioso- Lideres Religiosos _ Passei Direto.pdf

5 bloco 7 ano - Ensino Relogioso- Lideres Religiosos _ Passei Direto.pdf
Lista 02 exercícios de função do 1º grau (gabarito)
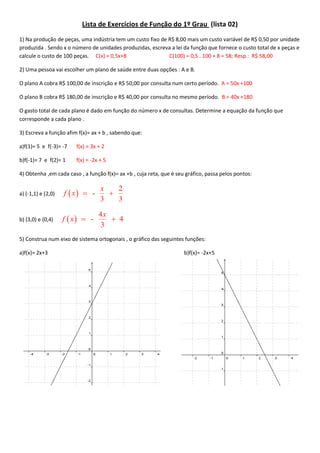
- 1. Lista de Exercícios de Função do 1º Grau (lista 02) 1) Na produção de peças, uma indústria tem um custo fixo de R$ 8,00 mais um custo variável de R$ 0,50 por unidade produzida . Sendo x o número de unidades produzidas, escreva a lei da função que fornece o custo total de x peças e calcule o custo de 100 peças. C(x) = 0,5x+8 C(100) = 0,5 . 100 + 8 = 58; Resp.: R$ 58,00 2) Uma pessoa vai escolher um plano de saúde entre duas opções : A e B. O plano A cobra R$ 100,00 de inscrição e R$ 50,00 por consulta num certo período. A = 50x +100 O plano B cobra R$ 180,00 de inscrição e R$ 40,00 por consulta no mesmo período. B = 40x +180 O gasto total de cada plano é dado em função do número x de consultas. Determine a equação da função que corresponde a cada plano . 3) Escreva a função afim f(x)= ax + b , sabendo que: a)f(1)= 5 e f(-3)= -7 f(x) = 3x + 2 b)f(-1)= 7 e f(2)= 1 f(x) = -2x + 5 4) Obtenha ,em cada caso , a função f(x)= ax +b , cuja reta, que é seu gráfico, passa pelos pontos: a) (-1,1) e (2,0) 2 - 3 3 x f x b) (3,0) e (0,4) 4 - 4 3 x f x 5) Construa num eixo de sistema ortogonais , o gráfico das seguintes funções: a)f(x)= 2x+3 b)f(x)= -2x+5
- 2. 6) Um corpo se movimenta em velocidade constante de acordo com a fórmula matemática s=2t-3, em que s indica a posição do corpo(em metros) no instante t (em segundos). Construa o gráfico de s em função de t. 7) O Custo de um produto é calculado pela fórmula C= 10+20q , na qual C indica o custo (em reais) e q a quantidade produzida (em unidades). Construa o gráfico de C em função de q. 8) Dado o gráfico da função de IR em IR , escreva a função f(x)= ax +b correspondente. 5 - 5 4 x f x x 3f x t S
- 3. 9) Considere as funções afins dadas por f(x) = -3x + 4 , g(x) = x/3 e h(x) = x - 2 Para cada uma das funções, responda: a) Em que pontos a reta correspondente corta os eixos x e y? b) A função é crescente ou decrescente? Função f(x) = -3x + 4 g(x) = x/3 h(x) = x - 2 Ponto que corta o eixo x (4/3 ; 0) (0 ; 0) (2 ; 0) Ponto que corta o eixo y (0 ; 4) (0 ; 0) (0 ; -2) Declividade decrescente crescente crescente 10) Determine a lei da função afim cuja reta intersecta os eixos em (-8,0) e (0,4). Essa função é crescente ou decrescente? 4 2 x f x Crescente
