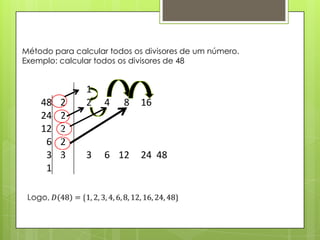
O documento discute conceitos de fatoração de números, potenciação, números primos, mínimo múltiplo comum (MMC) e máximo divisor comum (MDC). Explica como fatorar números, calcular potências, identificar números primos usando o Crivo de Erastóstenes, e métodos para calcular MMC e MDC. Inclui exemplos e exercícios destes conceitos.

1. Unidade 5 –
Parte 1
• Fatoração
• Mínimo múltiplo comum
– m.m.c.
• Máximo divisor comum –
m.d.c.

2. Potenciação de Números
Inteiros
Imagine a seguinte multiplicação
Nesta multiplicação, existem 10 fatores iguais. Assim, a
potenciação ou exponenciação, é uma forma de
reescrever uma multiplicação de vários fatores iguais de
uma forma “abreviada”

3. Numa multiplicação de vários fatores iguais, o fator que aparece
várias vezes, é chamado de base da potência; o expoente, é a
quantidade de fatores iguais.
• Base: Fator que aparece na
multiplicação
• Expoente: Quantidade de
fatores iguais.
• Potencia: Resultado.Leia “dois elevado a dez”

4. • Qualquer número elevado a 1 é ele mesmo
• Qualquer número não nulo elevado a zero vale 1
• Se multiplicarmos duas ou mais potências de mesma base,
basta conservarmos a base e somar os expoentes
• Se dividirmos duas ou mais potencias de mesma base,
basta repetirmos a base e subtrair os expoentes

5. Números primos
Um número é primo, se este possui somente dois divisores: o 1
e ele mesmo.
• O zero não é primo pois ele possui infinitos divisores
• O 1 não é primo pois seu único divisor é ele mesmo
• O 2 é primo pois seus divisores são o 1 e ele mesmo
• O 4 não é primo pois ele possui 3 divisores: o 1, 2 e ele mesmo
Em geral, os números que não são primos, são números
compostos

6. O Crivo de Erastóstenes

7. Vemos que o crivo de Erastóstenes nos fornece os primeiros
números primos entre 1 e 100.
São eles:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71,
73, 79, 83, 89 e 97
O 2 é o único número primo par

8. Fatoração de números Inteiros
A fatoração de um número inteiro é uma forma de se escrever
tal número como um produto entre números primos.
A fatoração é uma ferramenta importante para se obter o
mínimo múltiplo comum – m.m.c. de vários números, e também
o Máximo Divisor Comum entre vários números.

9. Método prático de fatoração
Fatorar o número 48
48 2
24 2
12 2
6 2
3 3
1 Acaba aqui

10. Exercícios
1- Apresente a forma
fatorada dos seguintes
números
a) 320 d) 640
b) 360 e) 400
c) 225 f) 220
2- Apresente a forma fatorada
dos seguintes números
a) 630 g) 900
b) 980 h) 240
c) 350 i) 960
d) 198 j) 2048
e) 860 k) 625
f) 270 l) 300

11. Mínimo Múltiplo Comum
O conceito de múltiplo
Assim, para se obter os múltiplos de um número qualquer, basta
multiplicar tal número por um outro número inteiro.

13. Múltiplo comum
Todos os elementos que pertençam ao mesmo tempo aos
conjuntos M(2) e M(3), são múltiplos comuns a 2 e 3. Assim,
Em um conjunto desses, o Mínimo Múltiplo Comum, será o menor
elemento do conjunto

14. Método prático para se calcular o m.m.c. de dois ou mais
números
Calcular o m.m.c. entre 36 e 48
36 48 2
18 24 2
9 12 2
9 6 2
9 3 3
3 1 3
1 1

15. Vemos aí que o 144 é realmente múltiplo de 36 e 48; além
disso, 144 é o menor múltiplo comum entre 36 e 48

16. Problema 1
Um automobilista dá uma volta completa na pista circular em 12
minutos, e um motociclista em 18 minutos. Suponha que os dois
veículos partiram às 8h00min. A que horas teremos o primeiro
encontro?
Temos na figura ao lado a pista. Sabe-se
que o automóvel cruza a linha de
chegada de 12 em 12 minutos, e a
motocicleta, de 18 em 18 minutos. Com
isso, basta calcular o mmc de 18 e 12.
Daí, mmc(12,18)=36. logo, os veículos
cruzarão a linha de chegada juntos às
8h36min

17. Exercícios
Calcule o m.m.c. dos elementos dos conjuntos a seguir

18. Máximo Divisor Comum – MDC
A ideia de divisibilidade
Um certo número é divísível por um outro número, se o resto dessa
divisão for 0 e o quociente for um número inteiro.
Exemplo: considere o número 36. Ele é divisível por 2, 3, 4, 6, 12,
18, 36.

19. Método para calcular todos os divisores de um número.
Exemplo: calcular todos os divisores de 48
1
48 2 2 4 8 16
24 2
12 2
6 2
3 3 3 6 12 24 48
1
/
/
/
/
/
/
/

20. Exercícios
Calcular todos os divisores dos números abaixo
a) 42 e) 56
b) 64 f) 72
c) 32 g) 49
d) 108 h) 96

21. Algoritmo de Euclides para cálculo do MDC de dois números
1 2
72 48 24
24 0
Quociente
O esquema acima, mostra o cálculo do MDC(48, 72).