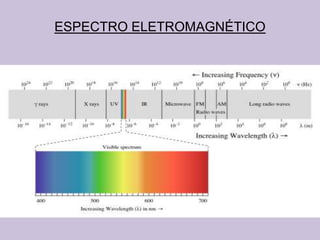
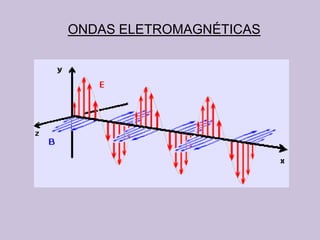
O documento discute as ondas eletromagnéticas, incluindo sua descoberta por Maxwell e suas propriedades como velocidade, campos elétrico e magnético perpendiculares, transporte de energia, pressão de radiação e exemplos de cálculos envolvendo intensidade, campo e força.

1. Ondas Eletromagnéticas

2. JAMES CLERK MAXWELL
(1831 – 1879)
•Foi o maior físico matemático desde Newton.
•Mostrou que uma carga elétrica oscilante produz dois campos
variáveis que se propagam simultaneamente pelo espaço.
•Criou a Teoria Eletromagnética da Luz, formulou equações
relacionando os campos elétricos e magnéticos, assim como as
relações entre as cargas e as correntes.

3. POR QUE ESTUDAR AS ONDAS
ELETROMAGNÉTICAS?
• A era da informação em que vivemos se baseia quase
integralmente na física das ondas eletromagnéticas.
• Nossos corpos são atravessados por sinais de rádio e
televisão.
•Microondas de radares e de sistemas de telefonia
celular podem nos atingir.
• Lâmpadas elétricas, máquinas de raios X, os
relâmpagos, etc.
• Somos banhados por ondas eletromagnéticas de todo
espectro.

4. ESPECTRO ELETROMAGNÉTICO

5. ONDAS ELETROMAGNÉTICAS
Maxwell mostrou que a velocidade das ondas
eletromagnéticas no vácuo deveria ser:
μ0 = 4π 10-7 N·A-2
“Esta velocidade é tão próxima da velocidade da luz que
parece que temos fortes motivos para concluir que a luz em si
(incluindo calor radiante, e outras radiações do tipo) é uma
perturbação eletromagnética na forma de ondas propagadas
através do campo eletromagnético de acordo com as leis
eletromagnéticas.” (1865)

6. PROPRIEDADES DAS ONDAS
ELETROMAGNÉTICAS
O comportamento do campo magnético é semelhante ao
do campo elétrico, porém em direções perpendiculares.
Os campos elétricos e magnéticos são perpendiculares à
direção de propagação da onda (onda transversal).
Os campos variam senoidalmente com a mesma
freqüência e estão em fase.

7. ONDAS ELETROMAGNÉTICAS

8. De acordo com essas propriedades, podemos
descrever os campos através de funções senoidais no
sentido da propagação da onda e do tempo:
E = Em sen(kx – ωt) (1)
B = Bm sen(kx – ωt) (2)
onde Em e Bm são as amplitudes dos campos;
ω é a frequência angular;
k é o número de onda.

9. A razão entre as amplitudes dos campos é:
Em = c (3)
Bm
Logo, dividindo a eq.(1) pela eq.(2) e substituindo a
eq.(3), temos:
E = c = 299.792.458 m/s (4)
B

10. ONDAS ELETROMAGNÉTICAS
Sendo v a velocidade de propagação de uma onda
eletromagnética, os vetores v, E, B devem ter, a cada
instante sentidos tais que obedeçam à regra da mão
esquerda.
v B
E
As ondas eletromagnéticas se propagam no vácuo.

11. TRASNPORTE DE ENERGIA E
VETOR DE POYNTING
Uma onda eletromagnética transporta energia e pode
fornecê-la a um corpo. Esta taxa de transporte de
energia é descrita por um vetor S, chamado de vetor de
Poynting, que é definido como:
SI: W/m2
Sua direção indica a direção de propagação da onda e
a direção de transporte de energia no ponto
considerado.

12. Como E e B são perpendiculares entre si, E x B = EB e
E= c B = E , assim:
B c
S = EB S = E2
0 c 0
Já a energia média transportada, denominada como
intensidade I da onda, é dada por:
I = Sméd = E2rms Erms = Em
c 0 212

13. A variação da intensidade I com a distância (por
exemplo, farol de um carro) é bem complicada.
Supomos uma fonte pontual que emite luz com a
mesma intensidade em todas as direções, ou seja, uma
superfície esférica de raio r e centro na fonte. Toda
energia emitida tem que passar pela superfície
esférica, assim:
I = potência = Ps = I
área 4 r2
Onde Ps é a potência da fonte e 4 r2 é a área da
superfície esférica.

14. EXEMPLOS
1) Uma lâmpada de 100W emite ondas
eletromagnéticas esféricas uniformemente
distribuídas em todas as direções. Achar a
intensidade a uma distância de 3m da lâmpada,
admitindo que a radiação eletromagnética seja
portadora de 50W de potência.
Sol.:
I = Ps = 50W I = 0,442W/m2
4 r2 4 (3)2

15. 2) Considerando que um observador esteja a 2m da
lâmpada no exercício anterior, calcule os valores rms
do campo elétrico e do campo magnético produzidos
pela fonte na posição do observador.
Sol.:
I = Ps = E2rms
4 r2 c 0
E2rms . 4 r2 = Ps . c 0
E2rms . 4 (2)2 = 50 . 3x108 . 4 x10-7 Erms = 19,37V/m
Como E/B = c
Brms = Erms/c Brms = 19,37/3x108 Brms = 6,4x10-8T

16. PRESSÃO DE RADIAÇÃO
Pode-se exercer pressão num corpo apenas iluminando-o.
Esta pressão de radiação indica que as ondas
eletromagnéticas possuem momento linear.
O módulo da variação deste momento linear do corpo está
relacionado com à variação de energia U que o corpo
recebe durante o intervalo de tempo t, que
matematicamente é dado por:
p= U (5)
c

17. A direção da variação do momento linear é a direção do
feixe incidente da radiação que o corpo absorve.
Todavia, se o feixe for só refletido, ou seja, não absorver
nenhuma radiação, a radiação é emitida novamente, logo:
p=2 U (6)
c
Caso a radiação seja parcialmente absorvida e
parcialmente refletida, o valor da variação do momento
linear será entre U/c e 2 U/c.

18. Sabemos que:
p=F. t (7)
ou F = p/ t (8)
E que a intensidade de radiação é dada por:
I = energia/tempo I = U/ t
área A
U = IA t (9)

19. Caso a energia seja totalmente absorvida, substituindo a
eq.(9) na eq.(5), temos:
p = U/c
ou p = IA t (10)
c
Substituindo a eq.(10) na eq.(8), temos o módulo da força
sobre a superfície:
F= p F = IA t/c F = IA (11)
t t c

20. Caso a radiação seja totalmente refletida, a força será:
F = 2IA (12)
c
Caso a radiação seja parcialmente refletida e parcialmente
absorvida, o módulo da força será entre IA/c e 2IA/c.
Sabemos que a pressão é a força exercida por unidade de
área, assim, dividindo ambos os membros das eqs.(11)
(12) por A, temos:
F = IA/c pr = I e pr =2I
A A c c

21. EXEMPLOS
3) Uma onda eletromagnética tem a intensidade de
100W/m2. Achar a pressão de radiação e os campos rms
magnético e elétrico.
Sol.:
pr = I/c pr = 100/3x108 pr = 3,33x10-7N/m2
I = E2rms 100 = E2rms Erms = 194V/m
c 0 3x108.4 x10-7
Brms = Erms Brms = 194 Brms = 6,46x10-7T
c 3x108

22. 4) Uma onda eletromagnética de intensidade 200W/m2
incide normalmente sobre um cartão negro retangular, de
20x30cm, e que absorve toda a radiação. Achar:
a) A força exercida pela radiação sobre o cartão;
b) A força exercida pela mesma onda se o cartão refletir
toda a radiação que sobre ele incide.
Sol.:
a) F = IA/c F = 200.6 F = 4x10-6N
3x108
a) F = 2IA/c F = 8x10-6N

23. 5) Achar a força exercida pela onda eletromagnética sobre
o cartão refletor da parte (b) do exercício anterior, se a
radiação incidir sob um ângulo de 30º com a normal do
cartão.
6) A amplitude de uma onda eletromagnética é E0 =
400V/m. Achar:
a) Erms e Brms;
b) a intensidade e a pressão de radiação.