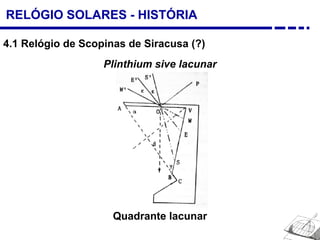
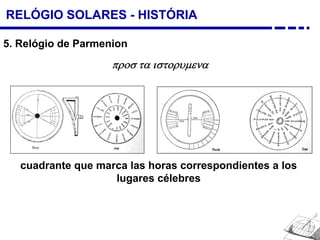
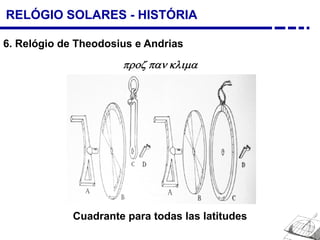
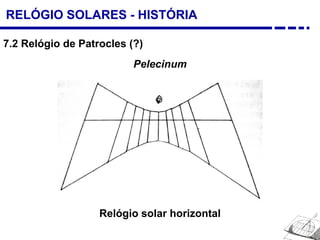
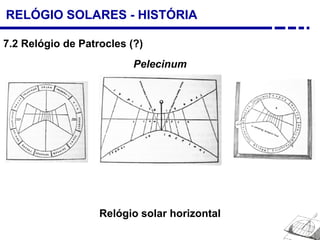
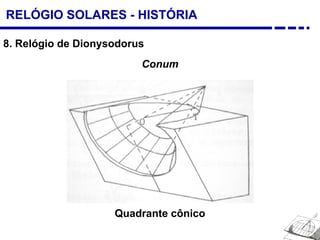
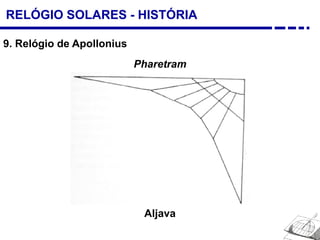
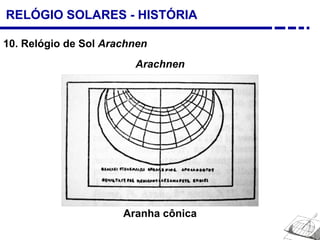
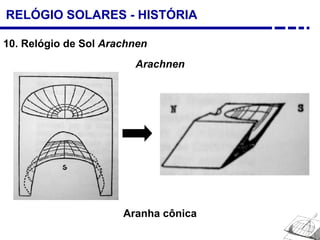
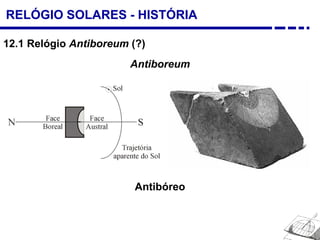
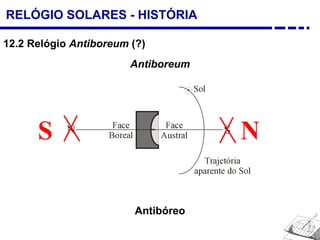
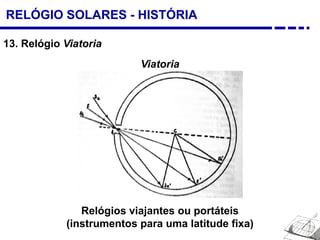
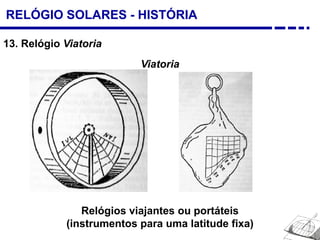
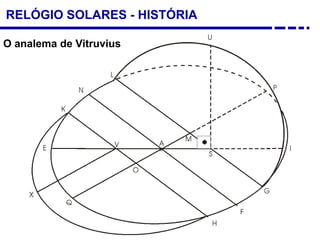
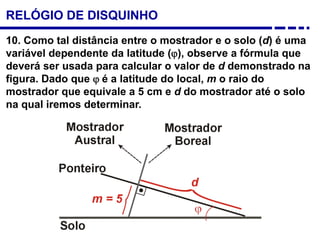
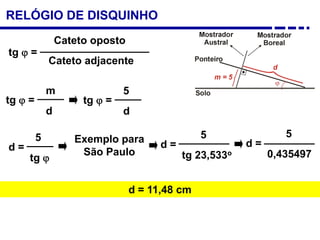
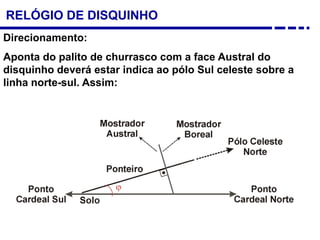
1. Uma breve história dos diferentes tipos de relógios solares inventados desde a antiguidade, incluindo o relógio semicircular de Berosus o Caldeu e o disco de Aristarchus de Samos.
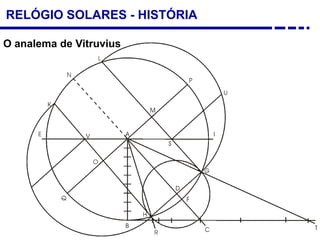
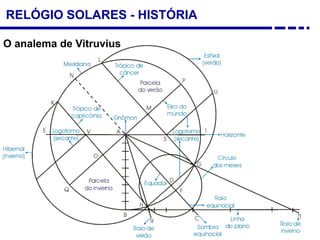
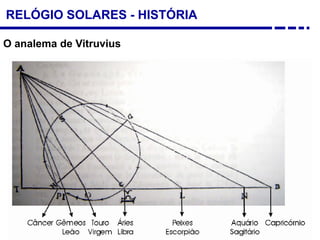
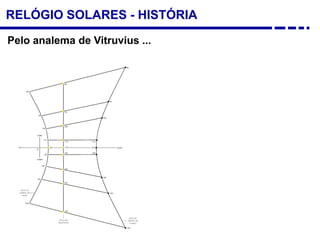
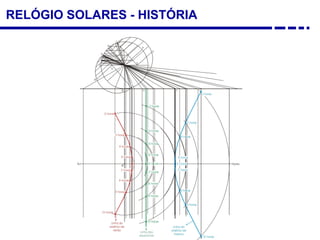
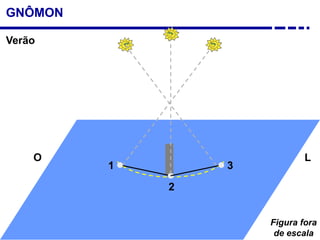
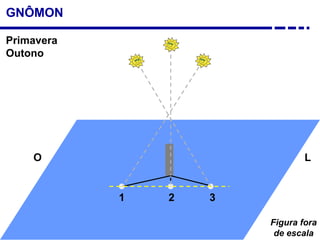
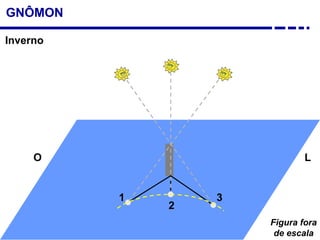
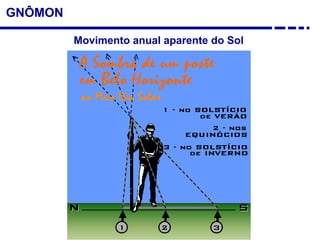
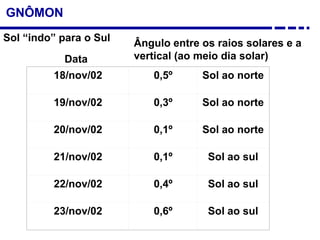
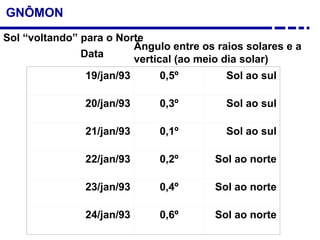
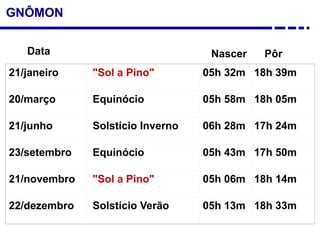
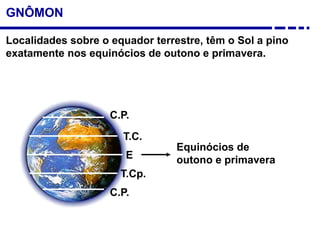
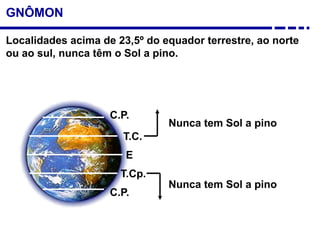
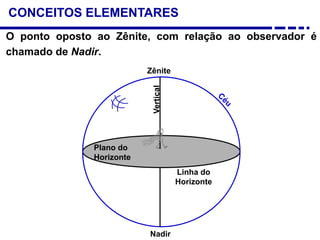
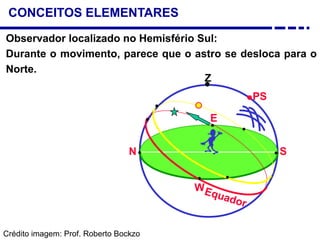
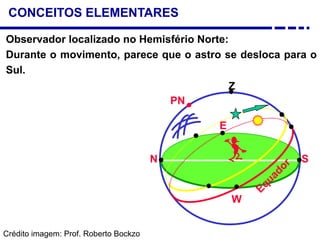
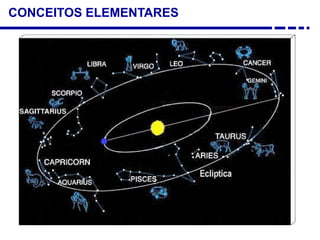
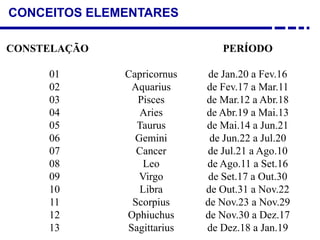
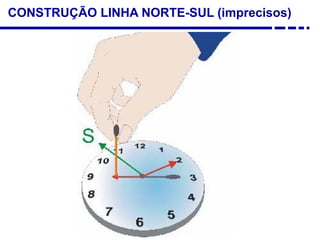
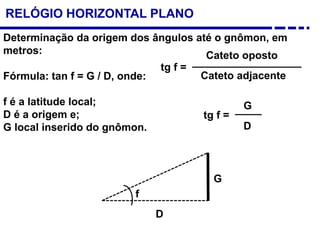
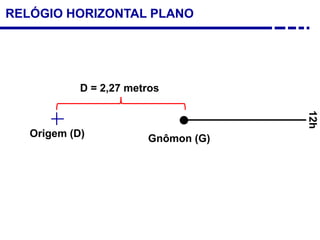
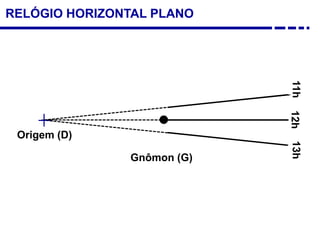
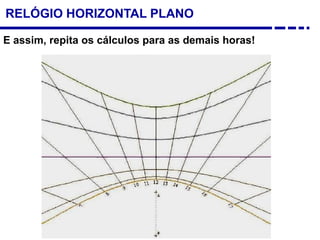
2. Explicação do movimento aparente do sol ao longo do dia e do ano observado através da sombra projetada pelo gnômon.
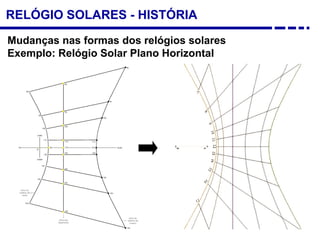
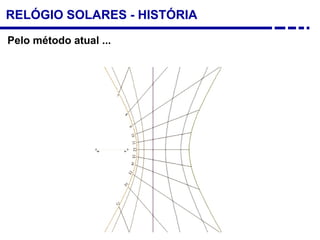
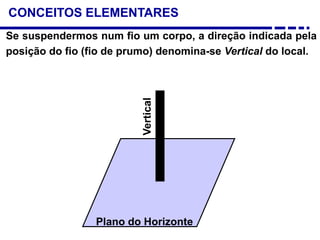
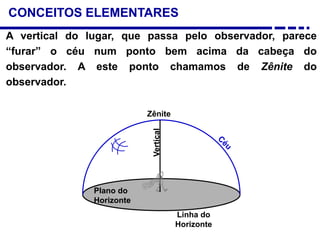
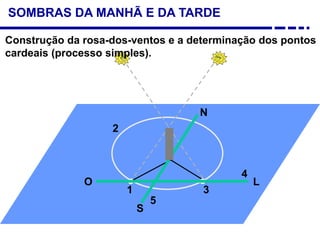
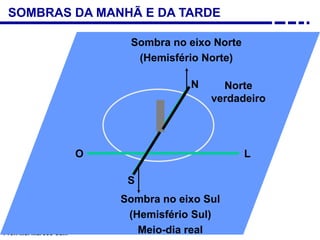
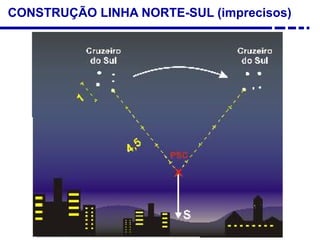
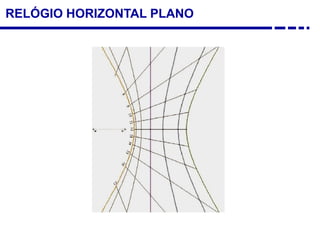
3. Diferentes tipos de relógios solares atuais como os horizontais, verticais e equatoriais.