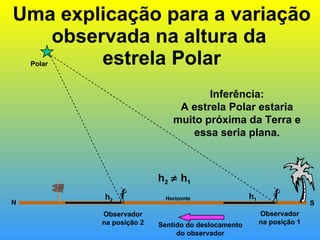
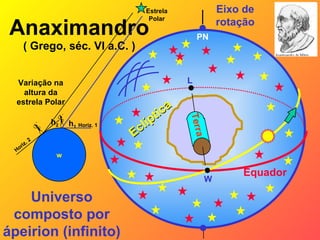
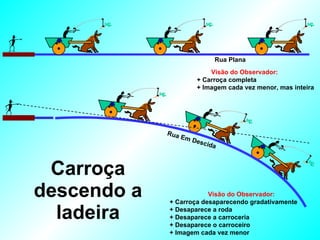
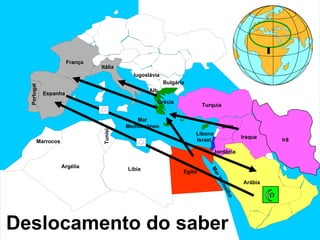
1) O documento descreve a evolução histórica das ideias sobre a estrutura do universo na astronomia antiga, desde as primeiras observações até o sistema heliocêntrico de Copérnico.
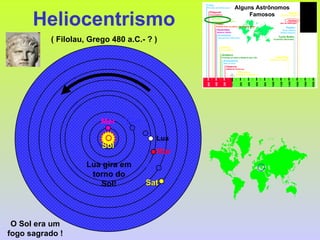
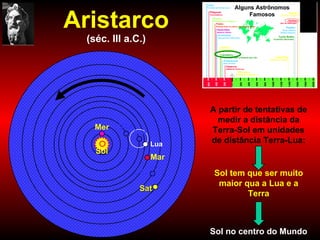
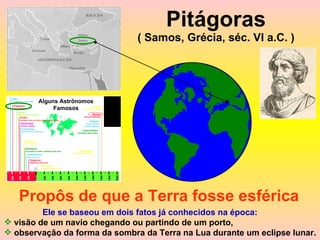
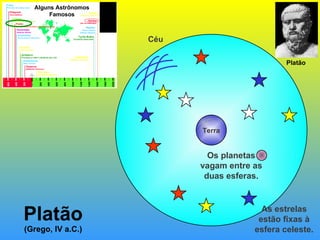
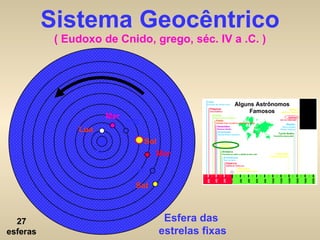
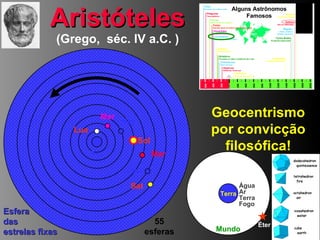
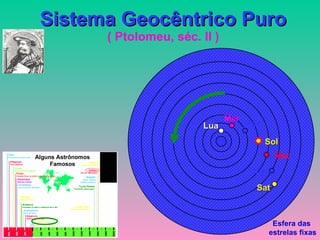
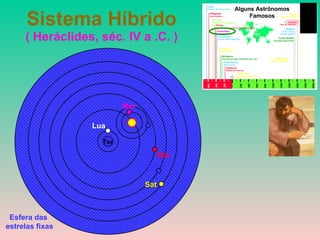
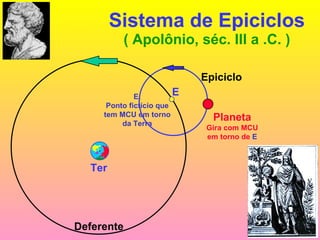
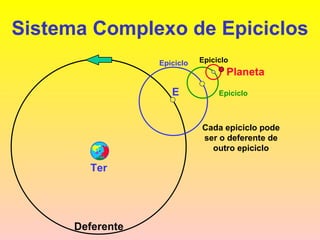
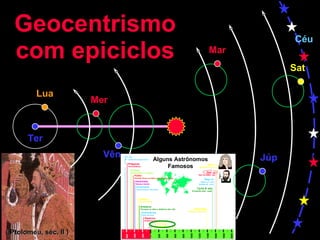
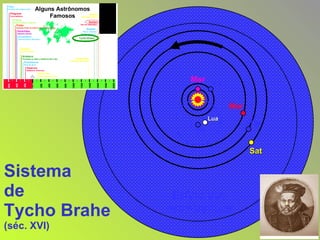
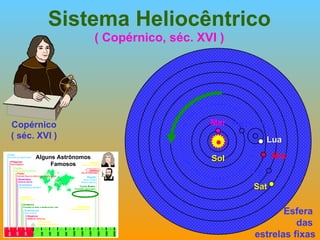
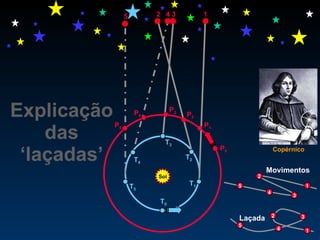
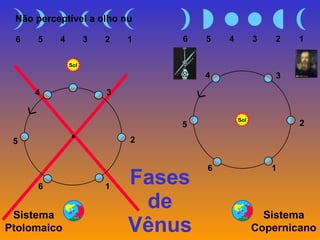
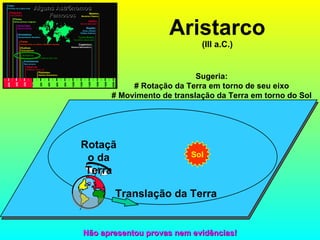
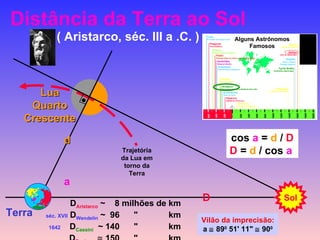
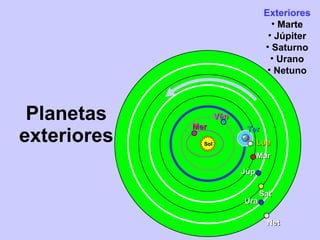
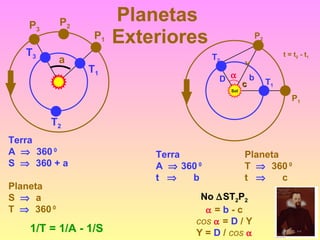
2) Foram propostos vários modelos como o geocêntrico de Ptolomeu, o híbrido de Heráclides e o heliocêntrico de Aristarco para explicar os movimentos celestes.
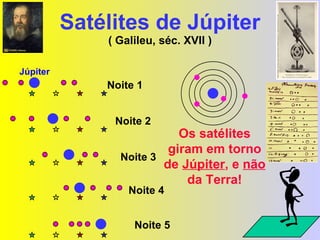
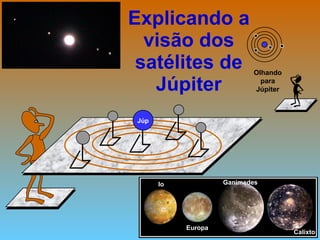
3) A introdução dos algarismos indo-arábicos e o uso do telescópio por Galileu foram fundamentais para























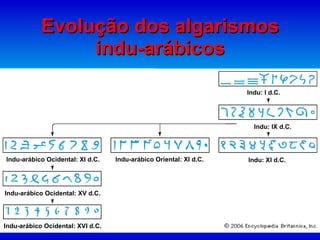












































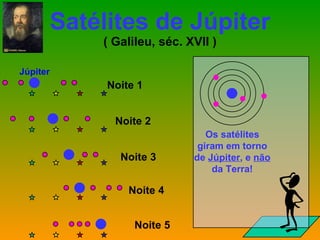





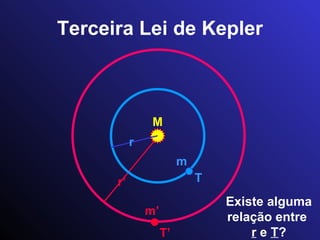
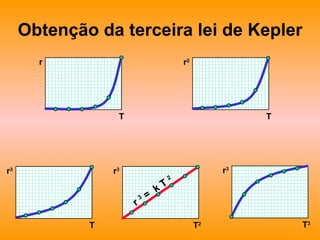
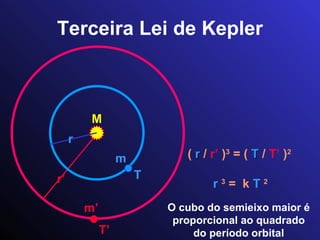
![Enunciado atual da Terceira Lei de Kepler ( r / r’ ) 3 = { ( M + m ) / ( M + m’ ) } x ( T / T’ ) 2 T’ m’ r’ M m r T r 3 = [G/(4 2 )] ( M + m ) T 2 Expressão correta: ( r / r’ ) 3 = ( T / T’ ) 2 r 3 = k T 2](https://image.slidesharecdn.com/estdisss-110228141245-phpapp02/85/Est-disss-143-320.jpg)

