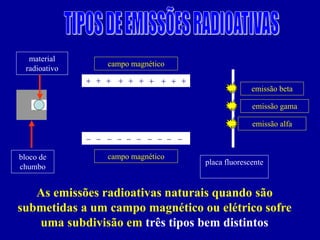
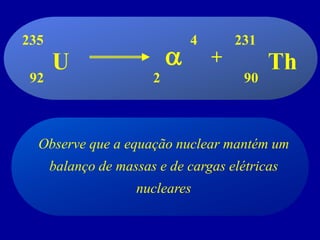
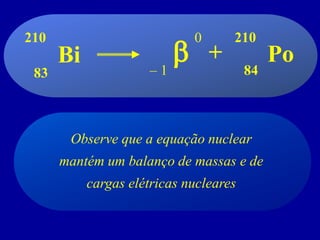
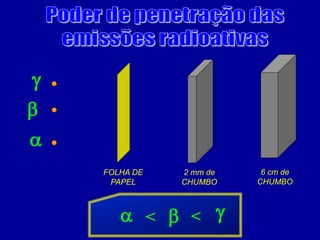
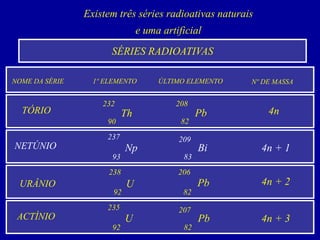
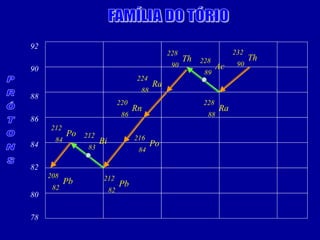
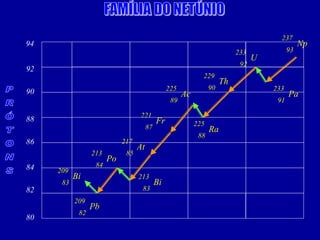
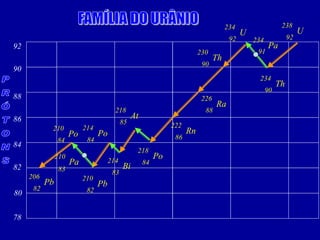
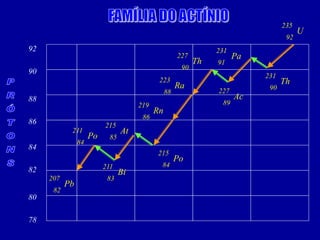
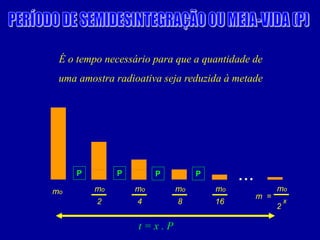
O documento discute o uso da radioatividade na medicina, agricultura, arqueologia, geologia e como fonte de energia. A radioatividade é usada no diagnóstico e tratamento de doenças, na datação de fósseis e rochas, e na geração de energia em reatores nucleares. Os principais tipos de radiação são alfa, beta e gama.

4. A RADIOATIVIADE NA MEDICINA
DIAGNÓSTICO DE DOENÇAS:
131
I
: Tireóide.
32
P
: Tumores dos olhos e câncer de pele.
197
Hg
: Tumores cerebrais.
24
Na
: Obstruções do sistema circulatório.
TRATAMENTO DE DOENÇAS:
60
Co
: câncer.
131
I
: câncer na tireóide.

5. Por meio da irradiação, carnes e frutas
podem ser esterilizados
(ficando livres de fungos e bactérias)
ou ser conservados por um tempo
mais prolongado
A RADIOATIVIADE NA AGRICULTURA

6. A RADIOATIVIDADE NA
ARQUEOLOGIA E GEOLOGIA
Os três métodos mais comuns de
DATAÇÃO
são os baseados nas seguintes desintegrações:
238
U
206
Pb
para
: usado na datação de rochas.
40
K
40
Ar
para
: usado na datação de rochas.

7. 14
C
14
N
para
: usado na datação de fósseis.

8. A RADIOATIVIDADE FONTE DE ENERGIA
REATORNUCLEAR:
É um dispositivo que permite controlar o
processo de fissão nuclear
A energia liberada durante o processo é usada para transformar água
líquida em vapor, que faz girar uma turbina, gerando energia elétrica

9. ARMAZENAMENTO DO LIXO NUCLEAR

10. ARMAS NUCLEARES

11. A radioatividade natural ocorre, geralmente, com os
átomos de números atômicos maiores que 82

12. É a propriedade que os núcleos instáveis possuem de emitir partículas e radiações eletromagnéticas,
para se tornarem estáveis

13. A reação que ocorre nestas condições, isto é, alterando o núcleo do átomo chama-se
REAÇÃONUCLEAR

14. As emissões radioativas
não são afetadas pelas variações de temperatura, pressão,
estado físico, etc

15. As emissões radioativas naturais quando são submetidas a um campo magnético ou elétrico sofre uma subdivisão em três tipos bem distintos
+
+
+
+
+
+
+
+
+
+
–
–
–
–
–
–
–
–
–
–
material
radioativo
bloco de
chumbo
campo magnético
campo magnético
placa fluorescente
emissão beta
emissão gama
emissão alfa

16. (a )
As partículas alfa possuem carga elétrica + 2,
devido aos prótons, e
massa igual a 4

17. (a )
São partículas constituídas por 2 PRÓTONSe 2 NÊUTRONS,
que são jogados, em alta velocidade, para fora de um núcleo instável

18. a
2
4

19. Em 1911, Frederick Soddy enunciou a
1ª LEI DA RADIOATIVIDADE
“Quando um núcleo emite
uma partícula alfa, seu
número atômico
diminui de duas unidades e seu número de massa
diminui de quatro unidades”

20. Observe que a equação nuclear mantém um balanço de massas e de cargas elétricas nucleares
U
Th
+
2
4
90
235
92
a
231

21. ( b )
São constituídas por
ELÉTRONS
atirados, em altíssima velocidade, para fora de um núcleo instável

22. –1
0
b

23. Como não existe elétron no núcleo, ele é formado a partir de um nêutron de acordo com o esquema:
O próton permanece no núcleo;
o elétron e o neutrino são atirados
para fora do núcleo
nêutron próton + elétron + neutrino
n
1
e
+
p
0
1
+1
0
–1
+
h
0
0

24. Soddy, Fajans, Russell enunciaram a
2ª LEI DA RADIOATIVIDADE
“Quando um núcleo emite uma partícula beta, seu número atômico
aumenta de uma unidade e
seu número de massa
permanece inalterado”

25. Bi
Po
84
210
83
210
–1
b
0
+
Observe que a equação nuclear
mantém um balanço de massas e de
cargas elétricas nucleares

26. As emissões gama
são ondas eletromagnéticas
semelhantes à luz
( g )
0
0
g

27. 01)(Covest-2004)Onúcleoatômicodealgunselementosé
bastanteinstávelesofreprocessosradioativospara
removersuainstabilidade.Sobreostrêstiposde
radiação,e,podemosdizerque:
b
a
g
Aoemitirradiação,umnúcleotemseunúmero
demassaaumentado.
0
0
a
1
1
Aoemitirradiação,umnúcleotemseunúmero
demassainalterado.
b
2
2
Aradiaçãoéconstituídapornúcleosdeátomosdehélio
a
3
Aoemitirradiação,umnúcleonãosofre
alteraçãoemsuamassa.
3
g
Aoemitirradiação,umnúcleotemseunúmeroatômicoaumentadoemumaunidade.
b
4
4

28. 02)Quandoumátomoemiteumapartículaalfae,em
seguida,duaspartículasbeta,osátomosiniciale
final:
a)Têmomesmonúmerodemassa.
b)Sãoisótoposradioativos.
c)Nãoocupamomesmolugarnatabelaperiódica.
d)Possuemnúmerosatômicosdiferentes.
e)Sãoisóbarosradioativos.
A
Y
X
Z
2
+
+
–1
0
b
a
2
4
Z’
A’
A = 4 + A’
Z = 2 –2 + Z’
Z = Z’
Têm mesmo número atômico e diferentes números de massa,
então, são ISÓTOPOS

29. 03) Ao se desintegrar, o átomo Rnemite 3 partículas
alfa e 4 partículas beta. O nº atômico e o nº de
massa do átomo final são, respectivamente:
86
222
a)84e210.
b)210e84.
c)82e210.
d)210e82.
e)86e208.
3
222
Rn
X
86
4
+
+
–1
0
b
a
2
4
Z
A
86 = 3 x2 + 4 x(–1) + Z
Z = 86 –2
Z = 84
86 = 6 –4 + Z
222 = 3 x4 + 4 x0 + A
222 = 12 + A
222 –12 = A
A = 210

30. 04)NatransformaçãoUemPb,quantaspartículas
alfaequantaspartículasbetaforamemitidaspor
átomodeurânioinicial?
92
238
82
206
a) 8 e 6.
b) 6 e 8.
c) 4 e 0.
d) 0 e 4.
e) 8 e 8.
82
206
x
238
U
Pb
92
y
+
+
–1
0
b
a
2
4
238 = 4 xx + 206
4 xx = 238 –206
4 xx = 32
x = 32 : 4
x = 8 partículas alfa
92 = 2 x8 –y+ 82
92 = 16–y+ 82
y = 98 –92
y = 6 partículas beta

31. 05)Nafamíliaradioativanaturaldotório,parte-sedotório,
Th,echega-senoPb.Osnúmerosdepartículas
alfaebetaemitidasnoprocessosão,respectivamente:
90
232
82
208
a)1e1.
b)4e6.
c)6e4.
d)12e16.
e)16e12.
82
208
x
232
Th
Pb
90
y
+
+
–1
0
b
a
2
4
232 = 4 xx + 208
4 xx = 232 –208
4 xx = 24
x = 24 : 4
x = 6 partículas alfa
90 = 2 x6 –y+ 82
90 = 12–y+ 82
y = 94 –90
y = 4 partículas beta

32. 06)(UFF-RJ)Dadaasériedourânioabaixorepresentada,assinale
aalternativaqueapresenta,respectivamente,onúmerode
nêutrons,prótonseelétronsemitidosnadesintegraçãodeum
núcleodeUatéPb.
92
238
82
206
a)32,32e10.
b)16,16e6.
c)10,10e5.
d)8,8e6.
e)8,8e5.
82
206
x
238
U
Pb
92
y
+
+
–1
0
b
a
2
4
238 = 4 xx + 206
4 xx = 238 –206
4 xx = 32
x = 32 : 4
x = 8 partículas alfa
92 = 2 x8 –y+ 82
92 = 16–y+ 82
y = 98 –82
y = 6 partículas beta
NÊUTRONS
8 x2= 16
PRÓTONS
8 x2= 16
ELÉTRONS
6 x1= 6

33. O poder de ionização das emissões
se encontra na seguinte
ordem crescente:
g
b
a
<
<

34. g
b
a
FOLHA DE
PAPEL
2 mm de
CHUMBO
6 cm de
CHUMBO
g
b
a
<
<

35. 01)Relacioneasradiaçõesnaturaisalfa,betaegamacom
suasrespectivascaracterísticas:
1.alfa.2.beta.3.gama.
Possui alto poder de penetração, podendo causar
danos irreparáveis ao ser humano.
3
2
3
1
São partículas leves, com carga elétrica negativa
e massa desprezível
São ondas eletromagnéticas semelhantes aos raios X, não possuem carga elétrica nem massa.
São partículas pesadas de carga elétrica positiva que, ao incidirem sobre o corpo humano, causam apenas queimaduras leves.
Aseqüênciacorreta,decimaparabaixo,é:
a)1,2,3,2.
b)2,1,2,3.
c)1,3,1,2.
d)3,2,3,1.
e)3,1,2,1.

36. É o conjunto de elementos que têm origem na emissão de partículas alfa e beta, resultando, como elemento final, um isótopo estável do chumbo

37. SÉRIES RADIOATIVAS
NOME DA SÉRIE
1º ELEMENTO
ÚLTIMO ELEMENTO
Existem três séries radioativas naturais
e uma artificial
Nº DE MASSA
TÓRIO
URÂNIO
ACTÍNIO
NETÚNIO
Th
Pb
232
90
82
208
4n
4n + 1
4n + 2
4n + 3
U
Pb
92
238
206
82
U
Pb
92
235
207
82
Np
Bi
93
237
209
83

38. Th
90
232
Ra
88
228
Ac
89
228
Th
90
228
Ra
88
224
Rn
86
220
Po
84
216
Pb
82
212
Bi
83
212
Po
84
212
Pb
82
208
78
80
82
84
86
88
90
92

39. Np
93
237
Pa
91
233
U
92
233
Th
90
229
Ra
88
225
Ac
89
225
Fr
87
221
At
85
217
Bi
83
213
Po
84
213
Pb
82
209
Bi
83
209
94
80
82
84
86
88
90
92

40. 78
80
82
84
86
88
90
92
U
92
238
Th
90
234
Pa
91
234
U
92
234
Th
90
230
Ra
88
226
Rn
86
222
Po
84
218
At
85
218
Bi
83
214
Po
84
214
Pb
82
210
Pa
83
210
Po
84
210
Pb
82
206

41. 78
80
82
84
86
88
90
92
U
92
235
Th
90
231
Pa
91
231
Ac
89
227
Th
90
227
Ra
88
223
Rn
86
219
Po
84
215
At
85
215
Bi
83
211
Po
84
211
Pb
82
207

42. Podemos identificar a série radioativa
de um nuclídeo através das expressões:
O número de massa (A) dos elementos desta
série é representado pela expressão:
A=4xn
Ra
236
236
4
59
:
=
comrestozero,istoé,
236=4x59

43. O número de massa (A) dos elementos desta
série é representado pela expressão:
A=4xn+2
Th
234
234
4
58
:
=
comresto2,istoé,
234=4x58+2

44. O número de massa (A) dos elementos desta
série é representado pela expressão:
A=4xn+3
Pa
234
231
4
57
:
=
comresto3,istoé,
231=4x57+3

45. É o tempo necessário para que a quantidade de uma amostra radioativa seja reduzida à metade
mo
mo
m
=
x
P
2
P
mo
4
P
mo
8
P
...
mo
16
mo
2
t = x . P

46. 01)Umasubstânciaradiativatemmeia-vidade8h.
Partindode100gdomaterialradiativo,que
massadasubstânciaradiativarestaráapós32h?
a)32g.
b)6,25g.
c)12,5g.
d)25g.
e)50g.
m
0
=
100g
t
=
32 h
P
=
8 h
m
=
?
m
=
x
mo
2
t = x . P
x = t : P
x = 32 : 8
x = 4
=
16
100
=
6,25g
100g
8 h
50g
8 h
25g
8 h
12,5g
8 h
6,25g
outro modo de fazer

47. 02)Oiodo125,variedaderadioativadoiodocom
aplicaçõesmedicinais,temmeia-vidade60dias.
Quantosgramasdoiodo125irãorestar,após6
meses,apartirdeumaamostracontendo2,0gdo
radioisótopo?
a)1,50g.
b)0,75g.
c)0,66g.
d)0,25g.
e)0,10g.
m
0
=
2,0 g
t
=
6 meses
P
=
60 dias
m
=
?
=
2 meses
=
=
3 meias-vidas
x
m
=
2
2
3
=
8
2
=
0,25g
6
2

48. 03)Umelementoradiativotemumisótopocuja
meia–vidaé250anos.Quepercentagemda
amostrainicial,desteisótopo,existirádepois
de1000anos?
a)25%.
b)12,5%.
c)1,25%.
d)6,25%.
e)4%.
m
0
=
100%
t
=
1000 anos
P
=
250 anos
m
=
?
=
=
4 meias-vidas
x
m
=
2
250
4
=
16
100
=
6,25%
1000
100

49. Verifica-se que o
PERÍODO DE SEMIDESINTEGRAÇÃO
ou
MEIA-VIDA
é aproximadamente 70%da VIDA MÉDIAdo respectivo isótopo radioativo

50. 01)Qualavida–médiadosátomosdeuma
amostraradioativa,sabendoque,em63hde
dedesintegração,40gdessaamostrasereduzem
a5g?
a)21h.
b)15h.
c)7h.
d)30h.
e)63h.
m
0
=
40g
t
=
63 h
P
=
m
=
5g
VM
=
?
40g
20g
10g
5g
P
P
P
x
=
3 meias-vidas
3
63
21 h
P
=
0,7
x
VM
=
21
=
0,7
x
VM
VM
=
21
0,7
=
30 h

51. O lançamento de partículas
contra o núcleo de um átomo, realizado em condições controladas de laboratório, transforma um átomo em outro
Esta transformação recebe o nome de
TRANSMUTAÇÃO ARTIFICIAL
N
O
2
2
a
4
2
+
+
p
1
1

52. É a divisão de um núcleo
em dois núcleos menores, com a liberação de uma quantidade
de energia muito grande
Uma fissão nuclear importante é reação que explica o princípio de funcionamento da bomba atômica
U
Kr
n
Ba
+
+
92
235
56
140
36
93
0
1
n
+
0
1
3

53. 01)(Covest–98)Umadasmaisfamosasreações
nucleareséafissãodourâniousadanabomba
atômica:
U
X
n
Ba
+
+
92
235
56
139
Z
A
0
1
n
+
0
1
3
QualovalordonúmeroatômicodoelementoX,
nestareação?
92
+
Z
56
=
–
Z
=
92
56
Z
=
36

54. 02)Nareaçãodefissão:
U
.......
n
Rb
+
+
92
235
37
90
Ce
a)
0
1
n
+
0
1
2
Oprodutoqueestáfaltandoéo:
b)
c)
d)
e)
La
Sm
Eu
Cs
144
58
146
57
160
62
157
63
144
55
X
Z
A
+
+
235
90
1
+
2
A
=
–
236
92
=
144
A
=
A
+
92
37
Z
=
–
92
37
Z
=
=
55
Z

55. É a junção de núcleos atômicos produzindo um núcleo maior,
com liberação de uma
grande quantidade de energia
Este processo ocorre no sol, onde núcleos de hidrogênio leve se fundem,
formando núcleos de hélio, com liberação de grande quantidade de energia
1
He
H
1
energia
+
4
2
4
b
+1
0
+
2

56. 01)Nareaçãodefusãonuclearrepresentadapor:
1
n
H
3
+
4
0
1
+
1
H
2
E
Ocorreliberaçãodeumnêutron(n).AespécieE
deveser:
a)2prótonse2nêutrons.
b)2prótonse3nêutrons.
c)2prótonse5nêutrons.
d)2prótonse3elétrons.
e)4prótonse3elétrons.
+
2
3
+
1
A
=
A
=
5
–
1
A
=
4
+
1
1
Z
=
Z
=
2
E
2
2 prótons
N
=
4
–
2
=
2 nêutrons

57. 02)(Covest–2006)Oselementosquímicos,emsua
maioria,foram,sintetizadosatravésdeprocessos
nuclearesqueocorrememestrelas.Umexemplo
estámostradonaseqüênciadereaçõesabaixo:
He
4
+
He
4
I )
Be
8
He
3
+
Be
8
II )
C
12
g
+
Destas reações, podemos afirmar que:
1)Sãoreaçõesdefissãonuclear.
2)Nareação(II),deveriaestarescritoHeno
lugardeHe.
3)HeeHesãoisótopos.
Está(ão) correta(s):
a)1,2e3
b)1apenas
c)3apenas
d)1e2apenas
e)2e3apenas
4
4
3
8
3
As reações produzem núcleos maiores
que os iniciais, então, é uma FUSÃO
F
+
3
=
12
+
0
se
4
V
São átomos de mesmo elemento
químico e diferentes números de
massa, então são ISÓTOPOS
V

58. 03)Nadeterminaçãodaidadedeobjetosque
fizerampartedeorganismosvivos,utiliza-seo
radioisótopoC,cujameia-vidaéemtornode
5700anos.Algunsfragmentosdeossos
encontradosemumaescavaçãopossuíamC
radioativoemquantidadede6,25%daquela
dosanimaisvivos.Essesfragmentosdevemter
idadeaproximadade:
14
14
a)5700anos.
b)11400anos.
c)17100anos.
d)22800anos.
e)28500anos.
100%
50%
25%
12,5%
6,25%
5700 a
x
5700
5700 a
5700 a
5700 a
t
=
4
22800 anos
t
=

59. 04)OacidentedoreatornucleardeChernobyl,em1986,
lançouparaaatmosferagrandequantidadedeSr
radioativo,cujameia-vidaéde28anos.Supondoser
esteisótopoaúnicacontaminaçãoradioativaeque
olocalpoderáserconsideradoseguroquandoa
quantidadeSrsereduzir,pordesintegraçãoa
1/16daquantidadeinicialmentepresente,olocal
poderáserhabitadonovamenteapartirdoanode:
38
90
38
90
a)2014.
b)2098.
c)2266.
d)2986.
e)3000.
mo
2
mo
28 anos
x
28
28 anos
28 anos
t
=
4
112 anos
t
=
mo
4
28 anos
mo
8
mo
16
Será habitado em:
1986
+
112
=
2098