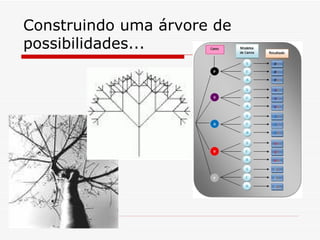
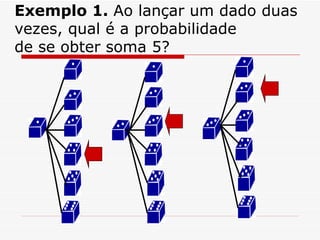
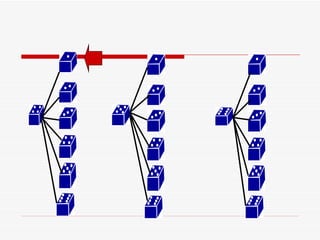
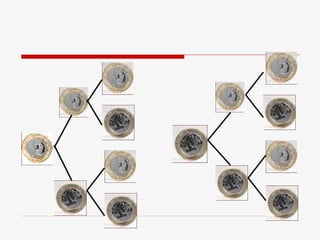
1) O documento discute a história da teoria das probabilidades e seu uso em jogos de azar, experimentos aleatórios e espaço amostral. 2) Experimentos aleatórios são aqueles que podem ter resultados diferentes sob condições iguais, enquanto o espaço amostral é o conjunto de todos os resultados possíveis. 3) O texto fornece exemplos de cálculo de probabilidades em jogos de dados e moedas, e desafios para determinar probabilidades em cartas e lançamento de moedas.

1. Probabilidade

2. Trabalho de Informática II Curso de Pós graduação em Novas Tecnologias do Ensino da Matemática UFF Prof. MacárioCosta Aluna: Lucia Regina Monteiro de Carvalho Grupo: Interatividade

3. A história da teoria das probabilidades, teve início com os jogos de cartas, dados e de roleta. Esse é o motivo da grande existência de exemplos de jogos de azar no estudo da probabilidade.

4. Experimento Aleatório É aquele experimento que quando repetido em iguais condições, podem fornecer resultados diferentes, ou seja, são resultados explicados ao acaso. Quando se fala de tempo e possibilidades de ganho na loteria, a abordagem envolve cálculo de experimento aleatório.

5. Espaço Amostral É o conjunto de todos os resultados possíveis de um experimento aleatório. A letra que representa o espaço amostral, é S.

6. Conceito de probabilidade Se em um fenômeno aleatório as possibilidades são igualmente prováveis, então a probabilidade de ocorrer um evento A é:

7. Construindo uma árvore de possibilidades...

8. Exemplo 1. Ao lançar um dado duas vezes, qual é a probabilidade de se obter soma 5?

10. Como

11. Exemplo 2.Uma moeda é lançada três vezes, sucessivamente. Qual a possibilidade de observarmos: a) apenas uma cara b) no máximo duas caras

13. Letra a) Aparecem apenas uma cara em 3 dos 8 casos possíveis, então temos:

14. Letra b) Temos no máximo duas caras ( pode ser 0, 1 ou 2 caras) em 7 dos 8 casos possíveis:

15. Agora é com você: Desafio 1. De um baralho de 52 cartas, uma é extraída ao acaso. Determine a probabilidade de: Sair o número 7 Sair um o nipe de paus Sair o 5 de espada

16. Desafio 2. No lançamento simultâneo de três moedas perfeitas distinguí-veis, qual é a probabilidade de serem obtidas: a)Pelo menos duas caras: b)exatamente duas caras: Faça com atenção, as respostas serão postadas no blog.

17. Bibliografia http://miltonborba.org/EST/Probabilidades.pdf www.somatemática.com.br Matemática Dante – Volume único Matemática completa – Giovanni, Bonjorno e Giovanni Jr – Volume ùnico Matemática – Gelson Iezzi – Volume único