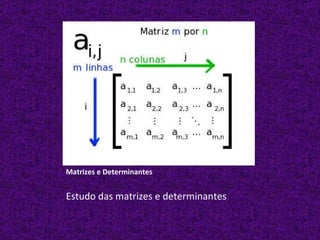
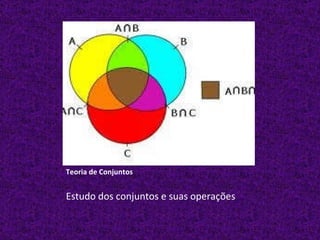
O documento discute o tópico da álgebra, definindo-a como a área da matemática que usa símbolos como letras para representar valores desconhecidos e resolver problemas. Explica como a álgebra é usada para representar situações da vida real e resolve um exemplo de equação algebraica. Também lista diversos outros tópicos matemáticos.

2. C.E.PADRE MADUREIRA THAIS SANTANA PILLER TURMA:801 PROFª.:VALÉRIA MATEMÁTICA TRABALHO SOBRE ÁLGEBRA ENTREGAR:18/05/2011

3. ...UMA AULA SOBRE... E COM VOCÊS...

5. O QUE É ÁLGEBRA? Para representar os problemas da vida real em linguagem matemática, muitas vezes utilizamos letras que substituem incógnitas (os valores que você não conhece, e quer descobrir). É aí que entram os famosos x, y, etc. O ramo da matemática que utiliza símbolos (normalmente letras do nosso alfabeto latino e do grego) para a resolução de problemas é chamado álgebra . As equações são a aplicação mais conhecida dessa área da matemática. Por exemplo, a área de um retângulo de base b e altura c é dada pela fórmula: A = b . c Esse monte de letra nada mais é que a representação de "fatos da vida real" por meio de números: a representa a área, b e c representam os lados do retângulo. Essa fórmula vale para qualquer retângulo cuja área se deseja calcular.

6. Letras substituem valores iguais Como você resolveria o seguinte cálculo? 3X + 7X Imagine que x represente um objeto, por exemplo, uma maçã. Então você faria: "3 maçãs mais 7 maçãs" Logicamente o resultado é "10 maçãs". Então: 3X + 7X = 10X O procedimento, como você viu, é simples: para somar números que acompanham incógnitas, basta somá-los, normalmente (desde que as incógnitas sejam iguais). Agora suponha que x valha 17 maçãs. O resultado de nossa operação seria 170.

7. Problemas resolvidos pela álgebra Vamos descobrir quanto medem os lados de um retângulo em que um lado é o dobro do outro e cujo perímetro é igual a 60. 2x x x 2x Para começar, é necessário saber o que é perímetro - é a soma de todos os lados de uma figura geométrica. Como um lado foi chamado de x, o outro - que é o dobro - será 2x. Nesse caso, o perímetro pode ser escrito como a soma dos 4 lados: P=X+X+2X+2X

8. A MATEMÁTICA EM NOSSA VIDA A Matemática está presente em diversas situações, se olharmos ao nosso redor, podemos notar sua presença nos contornos, nas formas dos objetos, nas medidas de comprimento, na escola, em casa, no lazer e nas brincadeiras. Seu desenvolvimento está ligado à pesquisa, ao argumento, ao interesse por descobrir o novo, investigar situações, é a ciência do raciocínio lógico. Desde a Antiguidade, a necessidade do homem de relacionar os acontecimentos naturais ao seu cotidiano despertou o interesse pelos cálculos e números. O surgimento do sistema de numeração decimal provocou um enorme avanço no desenvolvimento da Matemática, pois as teorias e aplicações podiam basear-se nos números, na busca por teses e comprovações. Atualmente, a Matemática consiste na ciência mais importante do mundo moderno, sendo abordada desde as séries iniciais. Sua relação com o cotidiano exige das pessoas um conhecimento mais amplo da disciplina, por isso devemos dar uma maior atenção ao seu estudo na escola. Algumas de suas aplicações estão relacionadas a financiamentos, compras parceladas, operações comerciais de compra e venda, construções, investimentos financeiros, aplicações bancárias, cálculos operatórios básicos, entre outros.Veja á seguir:

9. Trigonometria Tópicos sobre trigonometria no triângulo e no círculo.

10. Funções Estudo das funções e suas propriedades, construção e interpretação de gráficos.

11. Progressões Estudo da P.A e da P.G

12. Matemática Financeira Aqui você encontra tudo sobre matemática financeira.

13. Estatística Elementos da estatística descritiva

14. Geometria Plana Estudo das formas geométricas planas

15. Geometria Espacial Tópicos sobre geometria espacial

16. Geometria Analítica Definições e propriedades da Geometria Analítica

17. Números Complexos Conceitos e propriedades do conjunto dos números complexos

18. Matrizes e Determinantes Estudo das matrizes e determinantes

19. Equações e Inequações Equação, tipos de equações, resolução de equações, métodos para resolver equações.

20. Probabilidade Evento, espaço amostral, tipos de probabilidade, definições e propriedades

21. Polinômios Estudo dos polinômios

22. Produtos Notáveis Conheça os métodos para desenvolver todos os produtos notáveis

23. Logaritmos Definição e propriedades dos logaritmos

24. Análise Combinatória Fatorial, arranjo, combinação, permutação, teoria fundamental da contagem

25. Binômio de Newton Desenvolvimento do binômio de Newton, triângulo de Pascal, números binomiais...

26. Conjuntos Numéricos e suas Operações Números naturais, inteiros, racionais, irracionais, reais...

27. Sistemas Lineares Sistemas, solução de sistemas, sistemas homogêneos, classificação de um sistema, definição de sistemas lineares

28. Teoria de Conjuntos Estudo dos conjuntos e suas operações

29. Frações Definição de fração, operações envolvendo frações, números racionais.

30. FIM

31. BIBLIOGRAFIA http://WWW.ALUNOSONLINE.COM.BR