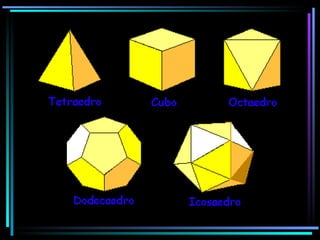
A interdisciplinaridade promove a integração entre disciplinas para fornecer uma visão holística do aprendizado. Isso envolve ligar áreas de conhecimento para criar uma rede de saberes que vai além da observação de cada disciplina isoladamente. A atividade proposta usa uma abordagem interdisciplinar entre matemática, história e artes para apresentar poliedros regulares, tendo os alunos construindo e analisando as propriedades geométricas de poliedros que eles mesmos criam.

1. Interdisciplinaridade e o Uso da Metodologia Interdisciplinar A interdisciplinaridade trata de uma visão educacional envolvendo as diversas áreas de estudo, no intuito de promover uma integração entre disciplinas e conteúdos, fazendo com que o processo de ensino-aprendizagem seja centrado em um visão na qual o ser humano aprende ao longo da sua vida, observando diversos pontos de observação. O homem passa a ser o criador de ligações entre as áreas de conhecimento e é essa ligação que ao interagir com outras viabiliza a criação de uma rede de saberes.

5. Prática da Interdisciplinaridade na Matemática O critério central é o da contextualização entre a Matemática e as diversas áreas do conhecimento. É importante definir o tema a ser trabalhado e saber o objetivo a ser alcançado com o trabalho realizado.

8. Atividade Proposta A atividade proposta tem como objetivo didático a apresentação dos Poliedros Regulares, também conhecidos como Poliedros de Platão, numa iniciativa interdisciplinar entre Matemática, História da Matemática e Educação Artística.