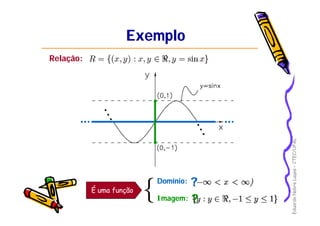
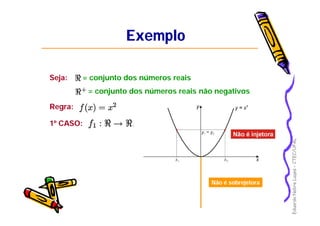
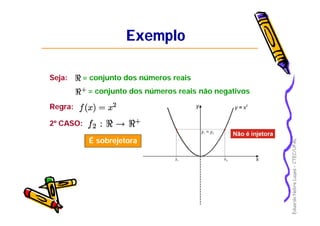
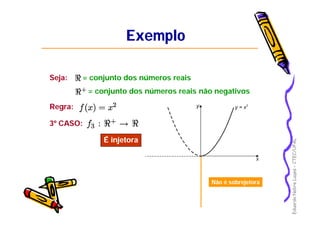
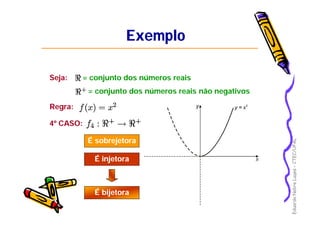
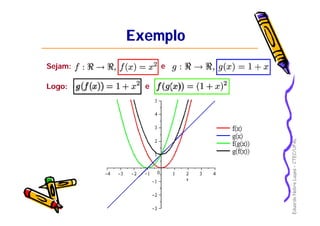
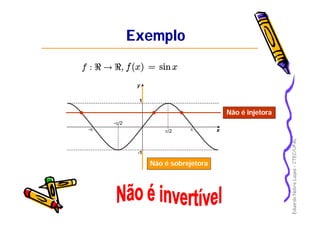
Este documento apresenta os principais conceitos de funções matemáticas, incluindo: 1) Definição de funções e suas partes como domínio, contradomínio e imagem; 2) Diferentes tipos de funções como injetora, sobrejetora e bijetora; 3) Propriedades especiais como função par, ímpar e monotônica. O documento fornece exemplos detalhados para ilustrar esses conceitos-chave.





![EduardoNobreLages–CTEC/UFAL
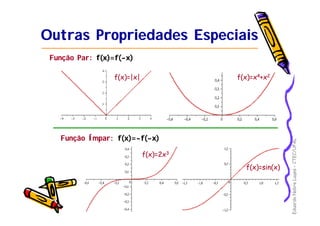
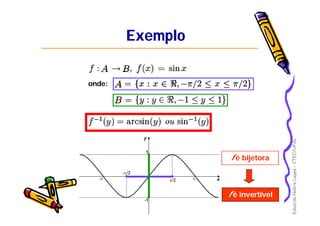
Outras Propriedades EspeciaisOutras Propriedades Especiais
Função nem par nem ímpar: f(x)=f(-x) e f(x)=-f(-x)
f(x)=sin(x)+xf(x)=sin(x)+x22
g(x)=[f(x)+f(g(x)=[f(x)+f(--x)]/2x)]/2
h(x)=[f(x)h(x)=[f(x)--f(f(--x)]/2x)]/2
Toda função, na pior das hipóteses, pode ser escritaToda função, na pior das hipóteses, pode ser escrita
como a soma de uma função par com uma função ímpar.como a soma de uma função par com uma função ímpar.
f(x)=g(x)+h(x)](https://image.slidesharecdn.com/2-funcoes-150910111347-lva1-app6892/85/funcoes-16-320.jpg)




![EduardoNobreLages–CTEC/UFAL
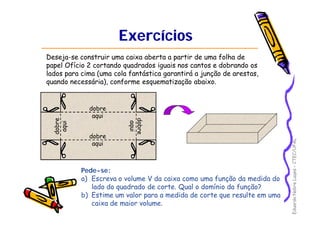
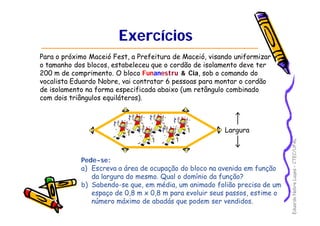
CurvasCurvas
Representação paramétrica:
],[ bat ∈
=
)(
)(
)(
)(
tz
ty
tx
tv
r
3
: ℜℜC
a b
A representação paramétrica
cria uma curva orientada
)(bv
r
)(av
r
)(tv
r
t
x
y
z
ℜ 3
ℜ](https://image.slidesharecdn.com/2-funcoes-150910111347-lva1-app6892/85/funcoes-26-320.jpg)
![EduardoNobreLages–CTEC/UFAL
CurvasCurvas
Exemplos:
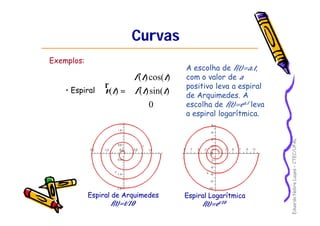
• Linha reta
+
+
+
=
tz
ty
tx
tv
γ
β
α
0
0
0
)(
r
Reta que passa pelo
ponto (x0, y0, z0) e que se
desenvolve na direção
do vetor (α, β, γ).
Reta passando pelo pontoReta passando pelo ponto (8,(8, --10, 6)10, 6) e possui a direçãoe possui a direção
do vetordo vetor ((--3, 4,3, 4, --2)2), com, com tt variando no intervalovariando no intervalo [0, 5][0, 5]..
x
y
z](https://image.slidesharecdn.com/2-funcoes-150910111347-lva1-app6892/85/funcoes-27-320.jpg)
![EduardoNobreLages–CTEC/UFAL
SuperfíciesSuperfícies
Representação paramétrica:
( )],[],[),( dcbaut ×∈
=
),(
),(
),(
),(
utz
uty
utx
utv
r
32
: ℜℜS
x
y
z
2
ℜ 3
ℜ
t
u
c
d
a b
),( utv
r](https://image.slidesharecdn.com/2-funcoes-150910111347-lva1-app6892/85/funcoes-29-320.jpg)
![EduardoNobreLages–CTEC/UFAL
SuperfíciesSuperfícies
Exemplos:
• Elipsóide
=
tc
utb
uta
utv
cos
sinsin
cossin
),(
r
Os coeficientes a, b e c
definem os semi-eixos
do elipsóide centrado na
origem. O domínio da
função é ([0,π]x[0,2π]).
Elipsóide centrado na origem e de semiElipsóide centrado na origem e de semi--eixos 3, 4 e 2,eixos 3, 4 e 2,
respectivamente nas direçõesrespectivamente nas direções xx,, yy ee zz..](https://image.slidesharecdn.com/2-funcoes-150910111347-lva1-app6892/85/funcoes-30-320.jpg)
