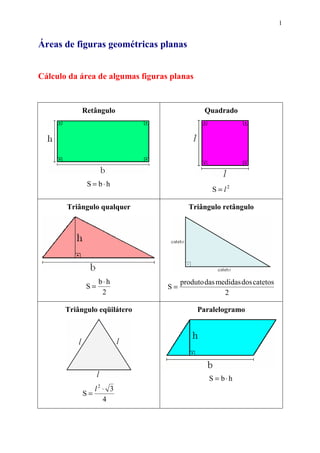
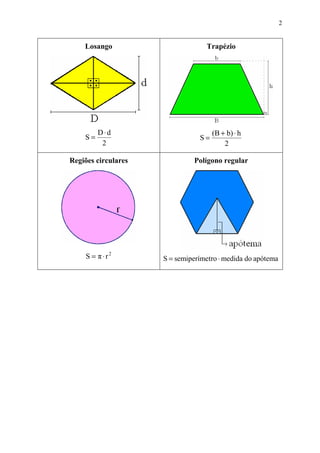
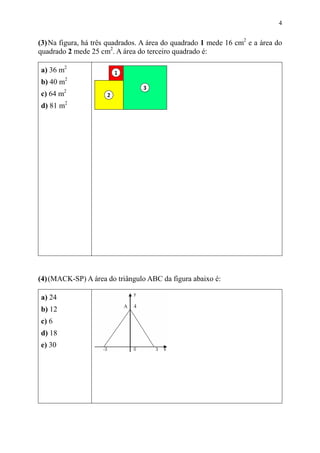
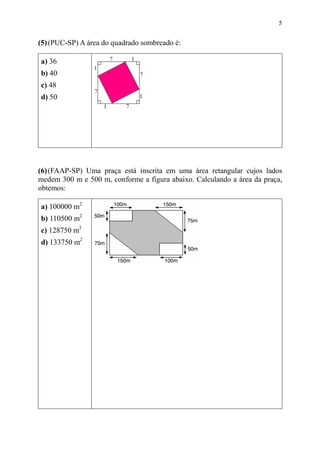
Este documento fornece fórmulas para calcular áreas de figuras geométricas planas como retângulos, quadrados, triângulos, paralelogramos, losangos, trapézios e figuras circulares. Ele também apresenta exercícios resolvidos como exemplos práticos para aplicar essas fórmulas.

1. Áreas de figuras geométricas planas
Profa. Dra. Denise Ortigosa Stolf
Sumário Página
Cálculo da área de algumas figuras planas ..................................................................... 1
Retângulo.................................................................................................................. 1
Quadrado .................................................................................................................. 1
Triângulo qualquer ................................................................................................... 1
Triângulo retângulo .................................................................................................. 1
Triângulo eqüilátero ................................................................................................. 1
Paralelogramo........................................................................................................... 1
Losango .................................................................................................................... 2
Trapézio.................................................................................................................... 2
Regiões circulares..................................................................................................... 2
Polígono regular ....................................................................................................... 2
Referências bibliográficas............................................................................................... 9

2. 1
Áreas de figuras geométricas planas
Cálculo da área de algumas figuras planas
Retângulo
hbS ⋅=
Quadrado
2
S l=
Triângulo qualquer
2
hb
S
⋅
=
Triângulo retângulo
2
catetosdosmedidasdasproduto
S =
Triângulo eqüilátero
4
3
S
2
⋅
=
l
Paralelogramo
hbS ⋅=

3. 2
Losango
2
dD
S
⋅
=
Trapézio
2
hb)(B
S
⋅+
=
Regiões circulares
2
rπS ⋅=
Polígono regular
apótemadomedidatrosemiperímeS ⋅=

4. 3
EXERCÍCIOS A
(1)(CESGRANRIO-RJ) Se as duas diagonais de um losango medem,
respectivamente, 6 cm e 8 cm, então a área do losango é:
a) 18 cm2
b) 24 cm2
c) 30 cm2
d) 36 cm2
(2)(CESGRANRIO-RJ) A área da sala representada na figura é:
a) 15 m2
b) 17 m2
c) 19 m2
d) 20 m2

5. 4
(3)Na figura, há três quadrados. A área do quadrado 1 mede 16 cm2
e a área do
quadrado 2 mede 25 cm2
. A área do terceiro quadrado é:
a) 36 m2
b) 40 m2
c) 64 m2
d) 81 m2
(4)(MACK-SP) A área do triângulo ABC da figura abaixo é:
a) 24
b) 12
c) 6
d) 18
e) 30

6. 5
(5)(PUC-SP) A área do quadrado sombreado é:
a) 36
b) 40
c) 48
d) 50
(6)(FAAP-SP) Uma praça está inscrita em uma área retangular cujos lados
medem 300 m e 500 m, conforme a figura abaixo. Calculando a área da praça,
obtemos:
a) 100000 m2
b) 110500 m2
c) 128750 m2
d) 133750 m2

7. 6
(7)(UFRGS-RS) A área do polígono da figura é 30. O lado x mede:
a) 3
b) 4
c) 5
d) 17
(8)Você quer fazer uma pipa em forma de losango, de tal forma que as varetas
meçam 75 cm e 50 cm. Nessas condições, quantos centímetros quadrados de
papel de seda você irá usar para fazer essa pipa?

8. 7
(9)Um hexágono regular está inscrito numa circunferência de raio 18 cm.
Nessas condições, determine:
a) a medida do lado desse hexágono;
b) o semiperímetro do hexágono;
c) a medida do apótema do hexágono;
d) a área desse hexágono.
(10) (ITE-SP) A área do círculo da figura é:
a) 2π m2
b) 4π m2
c) 6π m2
d) 9π m2

9. 8
(11) (UC-BA) Na figura abaixo temos dois círculos concêntricos, com raios
5 cm e 3 cm. A área da região sombreada, em cm2
, é:
a) 9π
b) 12π
c) 16π
d) 20π

10. 9
Referências bibliográficas
ANDRINI, Álvaro; VASCONCELLOS, Maria José. Novo praticando
matemática. São Paulo: Brasil, 2002.
BIGODE, Antonio José Lopes. Matemática hoje é feita assim. São Paulo:
FTD, 2006.
COLÉGIO ZACCARIA. Disponível em: <http:// www.zaccaria.g12.b>. Acesso
em: 12 de novembro de 2008.
DANTE, Luiz Roberto. Tudo é matemática. São Paulo: Ática, 2005.
EDIÇÕES EDUCATIVAS DA EDITORA MODERNA. Projeto Araribá:
Matemática. São Paulo: Moderna, 2007.
GIOVANNI, José Ruy; GIOVANNI JUNIOR, José Ruy. Matemática: pensar e
descobrir. São Paulo: FTD, 2005.
GIOVANNI, José Ruy; CASTRUCCI; Benedito; GIOVANNI JUNIOR, José
Ruy. A conquista da matemática. São Paulo: FTD, 1998.
GUELLI, Oscar. Matemática em construção. São Paulo: Ática, 2004.
GUELLI, Oscar. Matemática: uma aventura do pensamento. São Paulo:
Ática, 1998.
IMENES, Luiz Márcio; LELLIS, Marcelo Cestari. Matemática paratodos. São
Paulo: Scipione, 2006.
MIANI, Marcos. Matemática no plural. São Paulo: IBEP, 2006.
SÓ MATEMÁTICA. Disponível em: <http://www.somatematica.com.br>.
Acesso em: 23 de outubro de 2008.