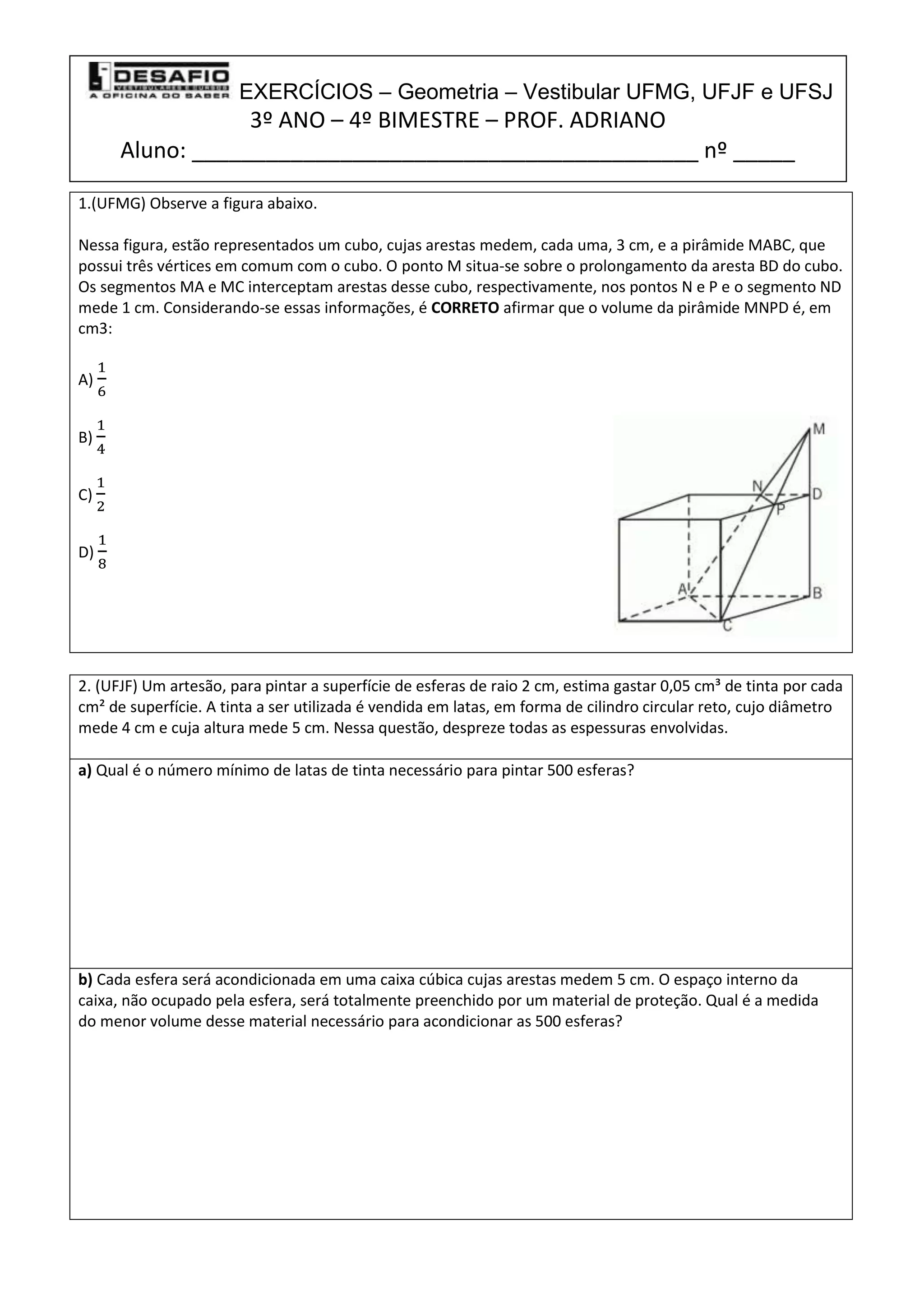
1) O documento apresenta 4 exercícios de geometria sobre cubos, esferas, pirâmides e volumes. 2) No primeiro exercício, é solicitado determinar o volume de uma pirâmide com vértices em comum a um cubo. 3) No segundo, calcula-se a quantidade de tinta necessária para pintar esferas e o volume para acondicioná-las. 4) Os outros exercícios pedem para calcular a altura, volume e valores possíveis de uma pirâmide dada sua base.

1. EXERCÍCIOS – Geometria – Vestibular UFMG, UFJF e UFSJ
3º ANO – 4º BIMESTRE – PROF. ADRIANO
Aluno: _________________________________________ nº _____
1.(UFMG) Observe a figura abaixo.
Nessa figura, estão representados um cubo, cujas arestas medem, cada uma, 3 cm, e a pirâmide MABC, que
possui três vértices em comum com o cubo. O ponto M situa-se sobre o prolongamento da aresta BD do cubo.
Os segmentos MA e MC interceptam arestas desse cubo, respectivamente, nos pontos N e P e o segmento ND
mede 1 cm. Considerando-se essas informações, é CORRETO afirmar que o volume da pirâmide MNPD é, em
cm3:
A)
B)
C)
D)
2. (UFJF) Um artesão, para pintar a superfície de esferas de raio 2 cm, estima gastar 0,05 cm³ de tinta por cada
cm² de superfície. A tinta a ser utilizada é vendida em latas, em forma de cilindro circular reto, cujo diâmetro
mede 4 cm e cuja altura mede 5 cm. Nessa questão, despreze todas as espessuras envolvidas.
a) Qual é o número mínimo de latas de tinta necessário para pintar 500 esferas?
b) Cada esfera será acondicionada em uma caixa cúbica cujas arestas medem 5 cm. O espaço interno da
caixa, não ocupado pela esfera, será totalmente preenchido por um material de proteção. Qual é a medida
do menor volume desse material necessário para acondicionar as 500 esferas?

2. 3. (UFMG)Uma pirâmide de base quadrada é construída recortando-se e dobrando-se uma cartolina quadrada
de 100 cm de lado, como mostrado nesta figura:
a) DETERMINE a altura da pirâmide em função de a.
b) DETERMINE o volume da pirâmide em função de a.
c) DETERMINE os valores de a para os quais se pode construir uma pirâmide da maneira descrita.
4. (UFSJ) Uma pirâmide com altura medindo 9 cm e cuja base é um hexágono com cm² de área foi
seccionada por um plano paralelo à base formando um tronco de pirâmide e uma nova pirâmide. Considere
que a área determinada pela secção plana é de 24 cm², assinale a alternativa que expressa o volume
CORRETO da piramide em cm³
A)
B) 72
C)
D)