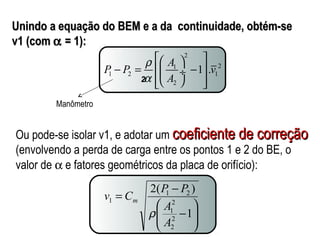
O documento discute diferentes tipos de medidores de pressão, velocidade e vazão, incluindo manômetros de tubo em U, placas de orifício, tubos de Venturi e Pitot. Explica os princípios de operação de cada um e fornece as equações chave para calcular a velocidade e vazão com base na perda de carga.

1. TTAA 663311 –– OOPPEERRAAÇÇÕÕEESS UUNNIITTÁÁRRIIAASS II
Aula 10: 13/04/2012
Medidores de pressão, velocidade e
vazão

2. Manômetro de Tubo em U
Consiste em um tubo de vidro em
forma de U, onde o fundo é
parcialmente preenchido com um
fluido de densidade rm.
Acima deste liquido, outro fluido
(geralmente ar) de densidade r.
As duas colunas, em geral, são de
comprimentos diferentes.
Se (P1 > P2 ) aumenta na coluna GD
do fluido de densidade rm e estabiliza
na posição H.
Aplicando a forma integrada da
Equação de Euler para fluidos
estacionários, obtemos

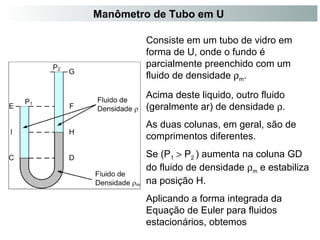
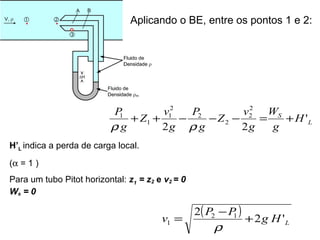
3. C D P =P
( ) 1 P P g EC C = +r
( ) ( ) 2 P P g GH g HD D m = +r +r
Resolvendo as equações anteriores e considerando que (EI)
= (FH)
e (IC) = (HD) obtemos
[( ) ( )] ( ) 1 2 P P g GH EC g HD m - =r - +r
g [(GF) (FH) (EI ) (IC)] g (HD) m =r + - - +r
g (GF) ( ) g (HD) m =r + r -r

4. Se as duas colunas são de tamanhos iguais (GF=0), temos
( ) ( ) 1 2 P P g HD m - = r -r
Deve ser mencionado que o termo da densidade do fluido
leve r pode ser desconsiderada quando comparada com a
densidade do fluido manométrico rm no caso de gases.
Se as colunas do manômetro são preenchidas com um
líquido, por exemplo água, r não pode ser negligenciado.

5. MMEEDDIIDDAA DDEE VVAAZZÃÃOO
AA ttaaxxaa ddee fflluuxxoo mmáássssiiccoo nnoo eessccooaammeennttoo ddee
llííqquuiiddooss ((ddmm//ddtt == vvρρAA)) éé pprraattiiccaammeennttee
ddeetteerrmmiinnaaddaa ppeellaa vveelloocciiddaaddee ddoo fflluuííddoo..
AA vveelloocciiddaaddee ddoo fflluuííddoo ddeeppeennddee ddoo ddiiffeerreenncciiaall
ddee pprreessssããoo qquuee ssee aapplliiccaa ppaarraa ffoorrççáá--lloo aa
eessccooaarr ppoorr uumm ttuubboo..
 SSee aa áárreeaa ddaa sseeççããoo ttrraannssvveerrssaall ddoo ttuubboo éé
ccoonnssttaannttee ee ccoonnhheecciiddaa,, ssee ssoouubbeerrmmooss oo vvaalloorr
ddaa vveelloocciiddaaddee mmééddiiaa ppooddeemmooss ccaallccuullaarr aa
vvaazzããoo vvoolluummééttrriiccaa..

6. A relação básica paarraa p ddeetteerrmmiinnaarr aa vvaazzããoo
ddoo llííqquuiiddoo éé::
VV == vv .. AA
oonnddee:: VV == vvaazzããoo vvoolluummééttrriiccaa
vv == vveelloocciiddaaddee mmééddiiaa ddoo eessccooaammeennttoo
AA == áárreeaa ddaa sseeççããoo ttrraannssvveerrssaall ddoo ttuubboo
CCoommoo aa vveelloocciiddaaddee ddoo fflluuiiddoo éé aaffeettaaddaa
 ppeellaa vviissccoossiiddaaddee,,
 ppeellaa ddeennssiiddaaddee,,
 ppeelloo aattrriittoo ccoomm aa ppaarreeddee,,
oo ddeesseemmppeennhhoo ddooss mmeeddiiddoorreess ddee vvaazzããoo éé
iinnfflluueenncciiaaddoo ppeelloo nnúúmmeerroo ddee RReeyynnoollddss..

7. m Os meeddiiddoorreess ddee vvaazzããoo ssee ccllaassssiiffiiccaamm ddee
aaccoorrddoo ccoomm oo mmééttooddoo ddee mmeeddiiççããoo::
11.. DDiiffeerreennççaa ddaa pprreessssããoo ((ppeerrddaa ddee ccaarrggaa))
22.. DDeessllooccaammeennttoo ppoossiittiivvoo
33.. VVeelloocciiddaaddee

8. 1. Medidor ddee vvaazzããoo ppoorr ppeerrddaa ddee ccaarrggaa
É o modelo mais usado.
Vantagens:
baixo custo e simplicidade
PPrriinnccííppiioo ddee ooppeerraaççããoo::
OOss mmeeddiiddoorreess ddee vvaazzããoo bbaasseeaaddooss nnaa ppeerrddaa ddee
ccaarrggaa ssããoo ddeessccrriittooss ppeellaa eeqquuaaççããoo ddee BBeerrnnoouullllii
((ddeerriivvaaddaa ddoo bbaallaannççoo ddee eenneerrggiiaa mmeeccâânniiccaa;; BBEEMM)),,
aapplliiccaaddaa aaoo eessccooaammeennttoo ddee uumm fflluuiiddoo ppaassssaannddoo ppoorr
uumm eessttrreeiittaammeennttoo eemm uumm ttuubboo..

9. A equação de Bernoulli ppaarraa uumm ttuubboo hhoorriizzoonnttaall ccoomm
aallgguummaa ppeerrttuurrbbaaççããoo ((bbaarrrreeiirraa ffííssiiccaa))..
Rearranjando a equação:
2 2
P v P v
1 + 1 = 2 +
2 r a r a
1 2 2 1 P P r v v
( 2 2 )
- = -
a
(PP11//ρρ11 ++ vv11
22//22αα ++ ZZ11)) ++ WWeeiixxoo == ((PP22//ρρ22 ++ vv22
22//22αα ++ ZZ22)) ++ EEff
2 2 2
AA eeqquuaaççããoo ddaa ccoonnttiinnuuiiddaaddee ((ddeerriivvaaddaa ddoo bbaallaannççoo ddee mmaassssaa))
ffoorrnneeccee aa sseegguuiinnttee rreellaaççããoo::
.
.
m =r v A
V = v A
1 1 2 2 v A =v A ( / ) 2 1 1 2 v = v A A

10. Unindo a equação do BEM e a ddaa ccoonnttiinnuuiiddaaddee,, oobbttéémm--ssee
vv11 ((ccoomm a == 11))::
2
P P A 1 .v
1 2
1 2 1
A
2
r
a
éæ ö ù
- = êç ¸ - ú
êëè ø úû
v C P P m
2( )
ö
÷ ÷ø
æ
ç çè
1 2
-
= -
1
2
1
A
2
2
1
A
r
2
Manômetro
Ou pode-se isolar v1, e adotar um ccooeeffiicciieennttee ddee ccoorrrreeççããoo
(envolvendo a perda de carga entre os pontos 1 e 2 do BE, o
valor de a e fatores geométricos da placa de orifício):

11. DDiissppoossiittiivvooss qquuee mmeeddeemm aa
vvaazzããoo ppeellaa ddiiffeerreennççaa ddee
pprreessssããoo oouu ccaarrggaa::
Orifício (A)
Tubo de Venturi (B)
Bocal (C)
Tubo de Pitot (D)
Medidor de cotovelo (E)

12. 1.1 Placa de Orifício
Os medidores de vazão ddee ppllaaccaa ddee oorriiffíícciioo ssããoo
mmaaiiss ccoommuunnss.. CCoonnssiisstteemm ddee uummaa ppllaaccaa ppllaannaa
ddee mmeettaall ccoomm uumm ffuurroo ddee ttaammaannhhoo ccoonnhheecciiddoo..
AAss ttoommaaddaass ddee pprreessssããoo aa ccaaddaa llaaddoo ddaa ppllaaccaa
ssããoo uussaaddooss ppaarraa ddeetteeccttaarr aa ppeerrddaa ddee ccaarrggaa..

13. GGeerraallmmeennttee oo ddiiââmmeettrroo ddaa ppllaaccaa ddee oorriiffíícciioo
ccoorrrreessppoonnddee aa ¼ ddoo ddiiââmmeettrroo ddoo ttuubboo::
1
4
D
D
orificio
b = =
tubo

14. EEqquuaaççããoo ppaarraa oo ccaallccuulloo ddee vv22 nnaa ppllaaccaa ddee oorriiffíícciioo::
v C P P o
2( )
ö
÷ ÷ø
= -
ç çè æ
1 2
-
2
2
A
2
1
2
1
A
r
V2 = v2 . A2
OOnnddee CCoo éé ddaaddoo ppeelloo sseegguuiinnttee ggrrááffiiccoo ::

15. Exemplo: Para Re = 1000 e razão diâmetro do orifício
e diâmetro do tubo de 0,60, Co = 0,77.

16. 1.2 Tubo de Venturi
Os tubos de Venturi têm a vantagem ddee aapprreesseennttaarr
bbaaiixxaass ppeerrddaass ddee ccaarrggaa.. AA ppeerrddaa ddee ccaarrggaa éé mmeennoorr
ppoorrqquuee nnããoo ooccoorrrree aa sseeppaarraaççããoo ddee uummaa ccaammaaddaa ddee
fflluuiiddoo ttuurrbbuulleennttaa,, ccoommoo ooccoorrrree nnaa ppllaaccaa ddee oorriiffíícciioo
OO mmeeddiiddoorr ddee VVeennttuurrii éé uumm ttuubboo ccoomm uummaa eennttrraaddaa
ccôônniiccaa ccuurrttaa ee uummaa ggaarrggaannttaa rreettaa ccoommpprriiddaa..
QQuuaannddoo oo llííqquuiiddoo ppaassssaa aattrraavvééss ddaa ggaarrggaannttaa,, ssuuaa
vveelloocciiddaaddee aauummeennttaa ccaauussaannddoo uummaa qquueeddaa ddee
pprreessssããoo

17. O tubo de Venturi pode ser usado com a maioria
dos líquidos, inclusive aqueles com alto conteúdo
de sólidos. Se usam para grandes vazões.
Medidor de Venturi

18. EEqquuaaççããoo ppaarraa oo ccaallccuulloo ddee vv22 nnoo VVeennttuurrii ((ggaarrggaannttaa))::
v C P P v
2( )
ö
÷ ÷ø
= -
ç çè æ
1 2
-
2
2
A
2
1
2
1
A
r
V2 = v2 . A2
OOnnddee CCvv éé ddaaddoo ppeelloo sseegguuiinnttee ggrrááffiiccoo::

20. 1.3. Tubo de Pitot
O Tubo de Pitot mede a velocidade.
Consiste em dois tubos concêntricos,
A e B, alinhados com a tubulação.
O interno é aberto na ponta  e o
externo conta com vários orifícios
pequenos ao lado, .
A leitura DH depende da velocidade do
fluido na tubulação acima do tubo A.
 


21. Aplicando o BE, entre os pontos 1 e 2:
P '
1 + + - - - = +
r r
H’L indica a perda de carga local.
(a = 1 )
Para um tubo Pitot horizontal: z1 = z2 e v2 = 0
Ws = 0
L
W
S H
g
g
Z v
P
g
g
Z v
g
2 2
2
2
2
2
2
1
1
( )
L v 2 P P 2g H' 2 1
1 = - +
r

22. A pressão P2 que resulta de levar um elemento de fluido no ponto 1 para o
repouso no ponto 2 é referida como pressão de impacto.
Desde que não temos nenhum meio eficiente para computar a perda de carga, H’L,
usualmente escrevemos a equação em termos de um fator denominado Cp
(“P” denota do tubo de Pitot), de acordo com a seguinte equação:
( )
v C 2 P P P
2 1
r
1
= - Em geral, a perda de carga entre os
pontos 1 e 2 é bem pequena e então o
valor de Cp é próximo a unidade.
O BE pode ser aplicado entre os pontos 1
e 3 para relacionar P1 e P3 (medidos pelo
manômetro) como
L
W
P '
S H
g
1 + + - - - = +
r r
g
Z v
P
g
g
Z v
g
2 2
2
3
3
3
2
1
1
Novamente, WS = 0, H’L @ 0 e, como os
tubos de Pitot são muito finos comparados
ao diâmetro da tubulação,
z1 @ z3 e v1 @ v3.

23. Isto conduz a
A equação manométrica aplicada a este sistema resulta em:
P P h( )g m - = D r -r 2 3
As equações anteriores podem ser modificadas para obter:
( ) ( )
v C g rm r h g m h
= 2 - D @ 2 r - r
D
1
r
r
P
1 3 P =P

24. Tubo de Pitot padrão

25. 2. Medidores de área variável (Rotâmetro)
Rotâmetro: um tubo cônico + um flutuador calibrado.
Quando não há fluxo de líquido, o
flutuador descansa livremente no fundo
do tubo. Quando o líquido entra pelo
fundo do tubo, o flutuador sobe.
A posição do flutuador varia com a
vazão que pode ser lida diretamente em
uma escala.
Sua exata posição é o ponto no qual a
diferença de pressões entre as
superfícies superior e inferior se
equilibram com o peso do flutuador.

26. Mais tipos de medidores de vazão:
2. Medidores de deslocamento positivo:
Medidores de pistão
Medidores de engrenagem
 Medidores de disco
 Medidores de palhetas rotativas
 Medidores helicoidais
palhetas engrenagem

27. 3. Medidores de velocidade:
Medidores de turbina
Medidores de vórtice
Medidores eletromagnéticos
Medidores ultra-sônicos
4. Medidores de massa: turbina
Medidores de Coriolis
Medidores térmicos
5. Medidores de Canal aberto

28. EExxeemmppllooss
Exemplo 1: Em uma trompa de vácuo de laboratório com as
dimensões da figura, escoa água com uma vazão de 2000
cm3/s.
Qual será a pressão na garganta?
Desconsidere as perdas friccionais.
A pressão no ponto 1 é 1,5 atm
33 ccmm 00,,77 ccmm
11 22
PP11 == 11,,55 aattmm

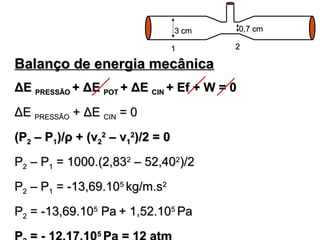
29. BBaallaannççoo ddee mmaassssaa
mm11== mm22 ++ ddmm//ddtt
mm11 == mm22
ρρ11..vv11..AA11 == ρρ22..vv22..AA22
vv11.. ππ((DD11
22))//44 == vv22.. ππ((DD22
22))//44
vv11 == vv22..DD22
22//DD11
22
33 ccmm 00,,77 ccmm
11 22
vv11 == vv22..((00,,000077))22//((00,,0033))22
vv== 00,,005544..vv..................................................................[[11]]

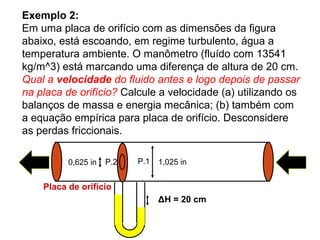
30. SSaabbeennddoo qquuee::
vv11 == VV//AA11
vv11 == 00,,000022//((ππ..((00,,0033))22//44))
vv11 == 22,,8833 mm//ss
SSuubbssttiittuuiinnddoo eemm [[11]] tteemm--ssee::
vv22 == 22,,8833//00,,005544
vv22 == 5522,,4400 mm//ss

31. 33 ccmm 00,,77 ccmm
11 22
BBaallaannççoo ddee eenneerrggiiaa mmeeccâânniiccaa
ΔΔEE PPRREESSSSÃÃOO ++ ΔΔEE PPOOTT ++ ΔΔEE CCIINN ++ EEff ++ WW == 00
ΔΔEE PPRREESSSSÃÃOO ++ ΔΔEE CCIINN == 00
((PP22 –– PP11))//ρρ ++ ((vv22 22
–– vv11
22))//22 == 00
PP22 –– PP11 == 11000000..((22,,883322 –– 5522,,440022))//22
PP22 –– PP11 == --1133,,6699..110055 kkgg//mm..ss22
PP22 == --1133,,6699..110055 PPaa ++ 11,,5522..110055 PPaa
PP22 == -- 1122,,1177..110055 PPaa == 1122 aattmm

32. Exemplo 2:
Em uma placa de orifício com as dimensões da figura
abaixo, está escoando, em regime turbulento, água a
temperatura ambiente. O manômetro (fluído com 13541
kg/m^3) está marcando uma diferença de altura de 20 cm.
Qual a velocidade do fluido antes e logo depois de passar
na placa de orifício? Calcule a velocidade (a) utilizando os
balanços de massa e energia mecânica; (b) também com
a equação empírica para placa de orifício. Desconsidere
as perdas friccionais.
0,625 in P.2 P.1 1,025 in
Placa de orifício
ΔH = 20 cm