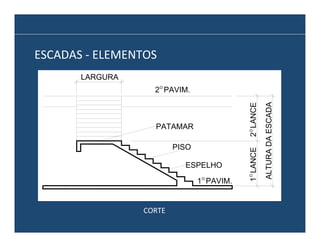
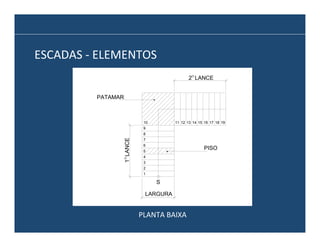
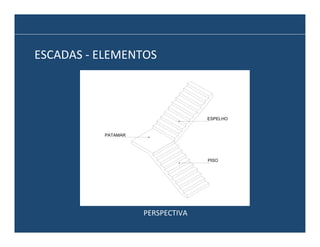
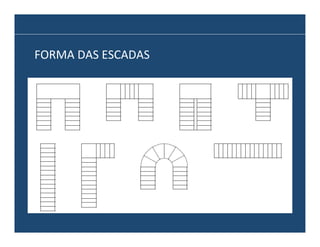
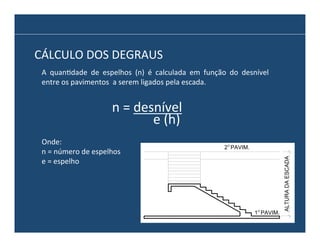
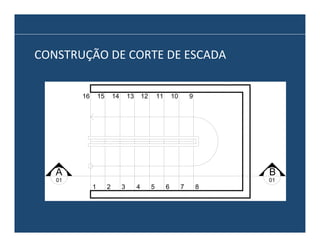
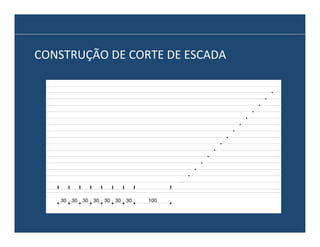
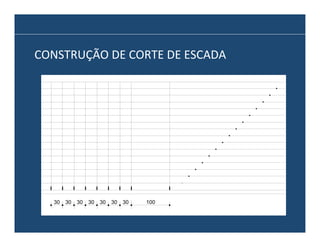
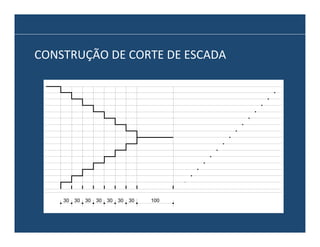
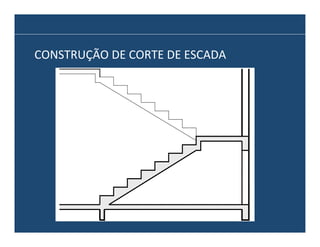
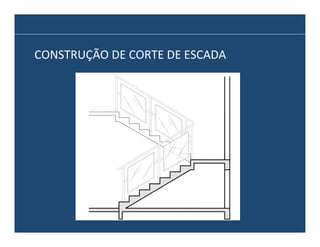
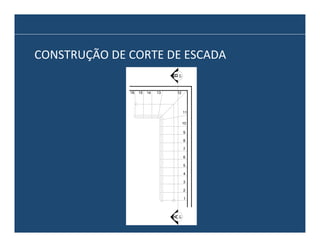
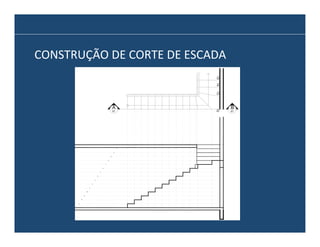
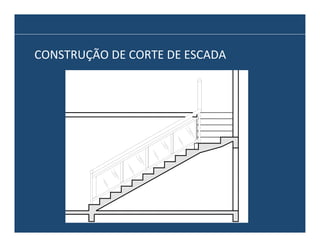
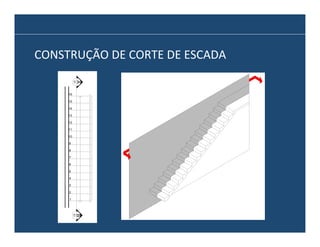
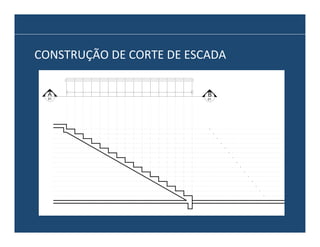
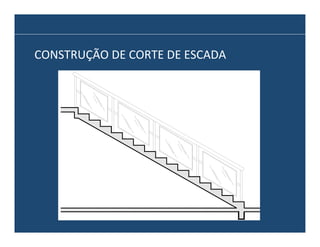
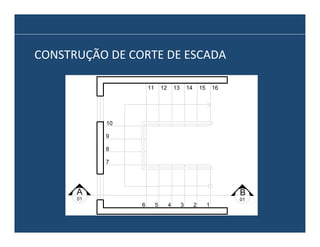
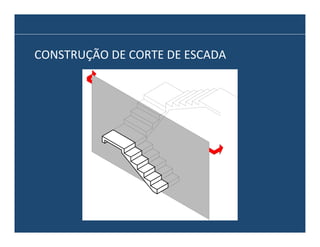
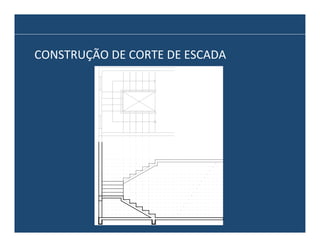
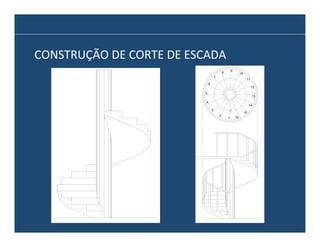
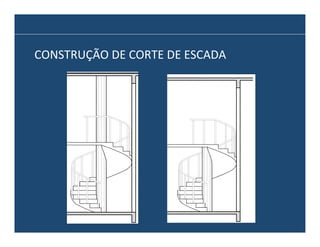
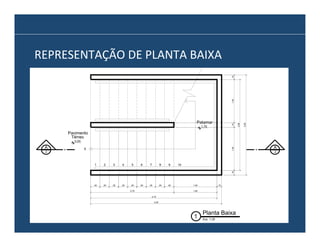
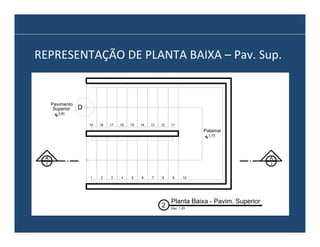
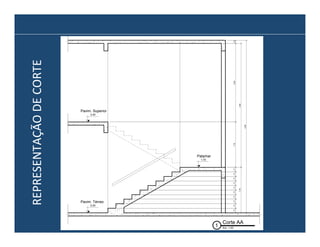
O documento descreve os principais elementos e métodos de projeto de escadas. Escadas são a forma mais comum de circulação vertical, sendo mais compactas que rampas e mais baratas que elevadores. Devem ser projetadas de modo a propiciar conforto e segurança aos usuários.

1. ESCADAS
–
CIRCULAÇÃO
VERTICAL

2. ESCADAS
Tipo
mais
comum
de
circulação
ver@cal,
por
ser
mais
compacta
que
a
rampa
e
mais
econômica
que
o
elevador.
Apesar
da
simplicidade
de
execução,
deve
ser
calculada
de
modo
adequado
a
fim
de
propiciar
o
maior
conforto
possível
ao
usuário.

3. ESCADAS
-­‐
ELEMENTOS
LARGURA
PISO
ESPELHO
1O PAVIM.
CORTE
ALTURA DA ESCADA
PATAMAR
1O LANCE
2O LANCE
2O PAVIM.

4. ESCADAS
-­‐
ELEMENTOS
2O LANCE
PATAMAR
10
11 12 13 14 15 16 17 18 19
9
1O LANCE
8
7
6
PISO
5
4
3
2
1
S
LARGURA
PLANTA
BAIXA

5. ESCADAS
-­‐
ELEMENTOS
ESPELHO
PATAMAR
PISO
PERSPECTIVA

6. ESCADAS
–
FORMA
DOS
DEGRAUS
As
formas
dos
degraus
podem
variar
bastante,
assim
como
o
material
que
é
construído
a
escada,
desde
que
se
garanta
sua
estabilidade,
conforto
e
segurança.

7. FORMA
DAS
ESCADAS
01
B
A
forma
das
escadas
é
escolhida
por
fatores
esté@cos
e
pelo
espaço
disponível
para
sua
construção.
A
existência
de
patamares
é
definida
pelo
código
de
obras
ou
por
bom
senso,
de
acordo
com
o
uso.
14
13
12
11
10
9
8
7
6
5
4
3
2
1
01
15
A
16
Forma
em
“L”

8. FORMA
DAS
ESCADAS
A
forma
das
escadas
é
escolhida
por
fatores
esté@cos
e
pelo
espaço
disponível
para
sua
construção.
A
existência
de
patamares
é
definida
pelo
código
de
obras
ou
por
bom
senso,
de
acordo
com
o
uso.
11
12
13
14
15
16
10
9
Forma
em
“U”
8
7
A
B
01
6
5
4
3
2
1
01

9. FORMA
DAS
ESCADAS
A
forma
das
escadas
é
escolhida
por
fatores
esté@cos
e
pelo
espaço
disponível
para
sua
construção.
A
existência
de
patamares
é
definida
pelo
código
de
obras
ou
por
bom
senso,
de
acordo
com
o
uso.
9
8
10
7
11
6
12
5
R i =20
13
4
14
3
2
15
1
16
Helicoidal

10. FORMA
DAS
ESCADAS

11. ESCADAS

12. ESCADAS

13. ESCADAS

14. ESCADAS

15. ESCADAS

16. ESCADAS

17. ESCADAS

18. ESCADAS

19. ESCADAS

20. ESCADAS

21. CÁLCULO
DOS
DEGRAUS
O
cálculo
é
realizado
baseado
na
fórmula
de
BLONDEL,
e
os
limites
mínimos
e
máximos
de
espelho
e
piso
são
definidos
pela
legislação
de
edificações.
2
e(h)
+
p
=
63
ou
64
Fórmula
de
Blondel
Onde:
e
=
espelho
p
=
piso
ESPELHO
PATAMAR
PISO

22. CÁLCULO
DOS
DEGRAUS
A
quan@dade
de
espelhos
(n)
é
calculada
em
função
do
desnível
entre
os
pavimentos
a
serem
ligados
pela
escada.
n
=
desnível
e
(h)
2O PAVIM.
1O PAVIM.
ALTURA DA ESCADA
Onde:
n
=
número
de
espelhos
e
=
espelho

23. CÁLCULO
DOS
DEGRAUS
–
ALTURA
LIVRE
Nos
projetos
de
escada
é
necessário
examinar
a
altura
livre
de
passagem.
Trata-­‐
se
da
distância,
medida
na
ver@cal,
entre
o
piso
do
degrau
e
o
teto.
Ou
seja,
a
laje
intermediária
entre
um
pavimento
e
o
outro.
Esta
altura
nunca
deve
ser
inferior
a
2,00
m
(dois
metros).

24. EXEMPLO
Calcular
as
dimensões
de
uma
escada
para
cobrir
um
desnível
de
2,90m.
Desnível
=
2,90
m
e
=
16
cm
(valor
arbitrário)
Número
de
espelhos
2
e(h)
+
p
=
64
2
x
16
+
p
=
64
32
+
p
=
64
p
=
64
–
32
p
=
32
n
=
desnível
e(h)
n
=
290
16
n
=
18,125

25. EXEMPLO
Calcular
as
dimensões
de
uma
escada
para
cobrir
um
desnível
de
2,90m.
Número
de
espelhos
(n)
=
18,125
O
NÚMERO
DE
ESPELHOS
NÃO
PODE
SER
QUEBRADO
Adotamos
18
para
o
número
de
espelhos
e
calculamos
a
altura
do
espelho
(e):
e(h)
=
desnível
n
e(h)
=
290
18
e(h)
=
16,11
cm

26. CONSTRUÇÃO
DE
CORTE
DE
ESCADA
16
15
14
13
12
11
10
9
A
01
B
1
2
3
4
5
6
7
8
01

27. 18
19
20
CONSTRUÇÃO
DE
CORTE
DE
ESCADA
2
3
4
5
6
7
8
9
h
10
11
12
13
14
15
16
17
altura do nível 2º pavimento
0
1
altura do nível 1º pavimento

28. 18
19
20
CONSTRUÇÃO
DE
CORTE
DE
ESCADA
2
3
4
5
6
7
8
9
h
10
11
12
13
14
15
16
17
altura do nível 2º pavimento
0
1
altura do nível 1º pavimento

29. CONSTRUÇÃO
DE
CORTE
DE
ESCADA
30
30
30
30
30
30
30
100

30. CONSTRUÇÃO
DE
CORTE
DE
ESCADA
30
30
30
30
30
30
30
100

31. CONSTRUÇÃO
DE
CORTE
DE
ESCADA
30
30
30
30
30
30
30
100

32. CONSTRUÇÃO
DE
CORTE
DE
ESCADA

33. CONSTRUÇÃO
DE
CORTE
DE
ESCADA

34. 01
B
CONSTRUÇÃO
DE
CORTE
DE
ESCADA
14
13
12
11
10
9
8
7
6
5
4
3
2
1
01
15
A
16

35. CONSTRUÇÃO
DE
CORTE
DE
ESCADA
15
14
13
01
12
A
B
01

36. CONSTRUÇÃO
DE
CORTE
DE
ESCADA

37. CONSTRUÇÃO
DE
CORTE
DE
ESCADA
01
A
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
B
01

38. CONSTRUÇÃO
DE
CORTE
DE
ESCADA
A
01
B
01

39. CONSTRUÇÃO
DE
CORTE
DE
ESCADA

40. CONSTRUÇÃO
DE
CORTE
DE
ESCADA
11
12
13
14
15
16
10
9
8
7
A
B
01
6
5
4
3
2
1
01

41. CONSTRUÇÃO
DE
CORTE
DE
ESCADA

42. CONSTRUÇÃO
DE
CORTE
DE
ESCADA

43. Arquiteto Me. Carlos Mariano Melo Júnior
CONSTRUÇÃO
DE
CORTE
DE
ESCADA

44. CONSTRUÇÃO
DE
CORTE
DE
ESCADA
9
8
10
7
11
6
12
5
R i =20
13
4
14
3
2
15
1
16

45. CONSTRUÇÃO
DE
CORTE
DE
ESCADA
9
8
10
7
11
6
12
5
13
4
14
3
2
15
1
16

46. CONSTRUÇÃO
DE
CORTE
DE
ESCADA
9
8
10
7
11
6
12
5
13
4
14
3
2
15
1
16

47. CONSTRUÇÃO
DE
CORTE
DE
ESCADA

48. 1,70
3,25
,15
Patamar
2,95
1,40
,15
REPRESENTAÇÃO
DE
PLANTA
BAIXA
Pavimento
Térreo
2
S
1
2
3
4
,30
,30
,30
,30
5
6
7
8
9
,30
,30
,30
,30
,30
10
,15
A
1,40
0,00
2,70
1,40
,15
1,40
4,10
4,25
1
Planta Baixa
Esc. 1:20
A
2

49. REPRESENTAÇÃO
DE
PLANTA
BAIXA
–
Pav.
Sup.
Pavimento
Superior
D
3,40
19
18
17
16
15
14
13
12
11
Patamar
1,70
A
A
2
2
1
2
3
4
5
6
7
8
2
9
10
Planta Baixa - Pavim. Superior
Esc. 1:20

50. ,17
0,00
,17
Pavim. Térreo
,17
,17
1
Esc. 1:20
,17
1,70
,17
,17
,17
,17
,17
1,70
6,46
4,64
2,94
REPRESENTAÇÃO
DE
CORTE
Pavim. Superior
3,40
Patamar
1,70
Corte AA
,12

51. EXERCÍCIO:
Desenvolva
em
planta
do
exercício
anterior,
uma
escada
que
deve
ter
um
corte
passando
sobre
ela
e
o
desenvolva.