O documento descreve conceitos básicos de equilíbrio líquido-vapor para misturas binárias ideais, incluindo:
1) Leis de Dalton e Raoult que regem o equilíbrio;
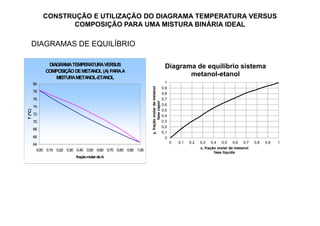
2) Construção de diagramas de equilíbrio temperatura vs composição;
3) Tipos de destilação como diferencial e flash.


![A PARTIR DAS LEIS DE DALTON E DE RAOULT, É POSSÍVEL OBTER A FRAÇÃO
MOLAR DE UM DOS COMPONENTES A PARTIR DOS VALORES DAS PRESSÕES
DE VAPOR E DA PRESSÃO TOTAL NO SISTEMA.
xA=(P-PB
0)/(PAº-PBº);
A FRAÇÃO MOLAR DE A NA FASE VAPOR PODE SER CALCULADA A PARTIR DA
SEGUINTE RELAÇÃO:
EQUILÍBRIO LÍQUIDO-VAPOR
LEIS DE DALTON E RAOULT
yA = PA/P = (PAº xA) / P
DEFINE-SE A VOLATILIDADE RELATIVA DE A PARA B (αAB) COMO SENDO:
αAB=PAº/PBº=[yA(1-xA)] / [xA(1-yA)]](https://image.slidesharecdn.com/equilibriodestilacao-150808181902-lva1-app6892/85/Equilibrio-destilacao-3-320.jpg)










![DESTILAÇÃO DIFERENCIAL - EQUACIONAMENTO PARA
MISTURAS BINÁRIAS
CASO PARTICULAR: VOLATILIDADE APROXIMADAMENTE CONSTANTE:
α=[y(1-x)] / [x(1-y)] y = αx/[1+(α-1)]
DESTA FORMA:
OU
OU AINDA:OU AINDA:
PARA MISTURA DE MULTICOMPONENTES IDEAL PODE-SE RELACIONAR
L, L0 DE DOIS ELEMENTOS QUAISQUER (i E j) E A RESPECTIVA
VOLATILIDADE RELATIVA :](https://image.slidesharecdn.com/equilibriodestilacao-150808181902-lva1-app6892/85/Equilibrio-destilacao-16-320.jpg)














































