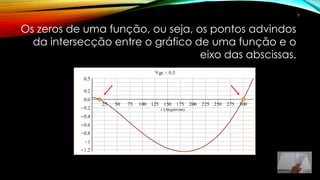
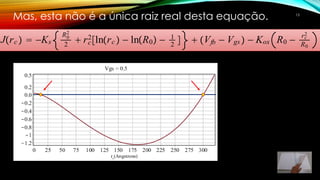
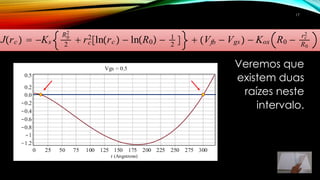
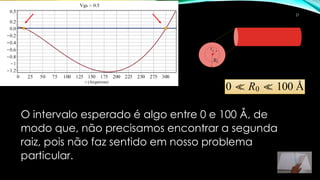
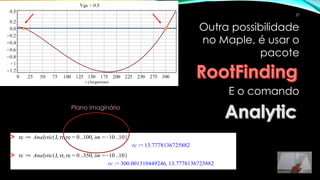
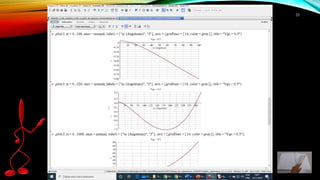
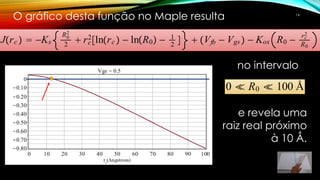
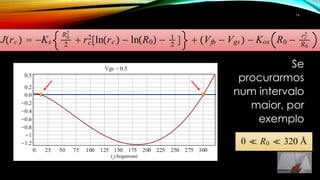
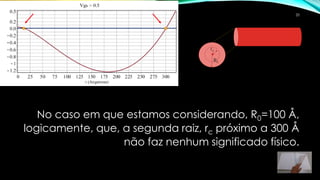
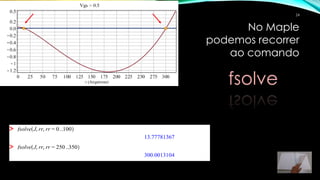
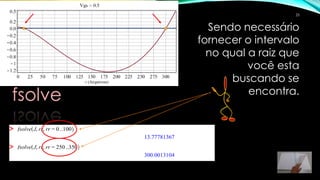
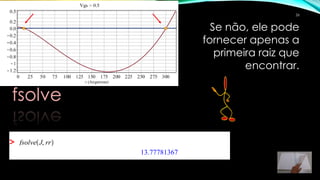
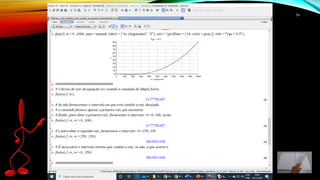
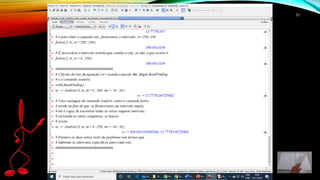
1) O documento discute como encontrar os zeros de uma função transcendental usando o software Maple. 2) A função é definida e graficada para identificar possíveis raízes. 3) Os comandos fsolve e NSolve do Maple podem ser usados para calcular as raízes numericamente, considerando o intervalo físico relevante.

1. Encontrando os zeros de
função com o Maple
Professora Dra. Regiane Aparecida Ragi Pereira

2. Uma ideia não se materializa facilmente.
Requer muito esforço e empenho constante.
2

3. Nesta apresentação
vamos discutir como
encontrar os zeros de uma
função transcendental
usando o Maple.
3

4. É muito comum
termos que
encontrar os zeros
de uma função...
4

5. Os zeros de uma função, ou seja, os pontos advindos
da intersecção entre o gráfico de uma função e o
eixo das abscissas.
5

6. Ks
R0
2
2
 rc
2
lnrc   lnR0  1
2
  Vfb  Vgs  Kox R0  rc
2
R0
Por exemplo, suponha que você tenha a função
transcendental acima, e queira descobrir a variável rC.
6

7. Nesta equação
existem
inúmeras
constantes
como serão
mostradas a
seguir.
 Ks
R0
2
2
 rc
2 lnrc   lnR0  1
2

 Vfb  Vgs  Kox R0 
rc
2
R0
7

8. Se não estiver interessado
na origem desta equação,
pule o próximo slide, slide
9, e vá para o Slide 10.

9. 9
Resumidamente, esta equação é
obtida quando resolvemos a equação
de Poisson em todo o espaço, para
uma estrutura que representa um
dispositivo de nanofio semicondutor
cilíndrico envolvido por uma camada
de óxido de certa espessura, e
seguidamente envolvido por uma
camada de material condutor,
denominado contato de gate, e
queremos encontrar o raio condutor
em função da tensão aplicada ao gate.
Regiane Ragi and Murilo Araujo Romero, Trans. on Nanotech., Vol. 18, pp. 762 – 769, July (2019).
z0 Lz
Source
c

10. Ks 
qNd
2s
q  0.16021764.1018 C
Nd  1.1019 cm
3
 1.1025 m
3
s  kdsem .0
kdsem  11.8
0  8.854187187.1012 F.m
1
Kox 
qNdwox
2ox
q  0.16021764.1018 C
Nd  1.1019 cm
3
 1.1025 m
3
wox  20 Å  20.10
-10
m
ox  kdox.0
kdox  3.9
0  8.854187187.1012 F.m
1
Ks 
qNd
2s
q  0.16021764.1018 C
Nd  1.1019 cm
3
 1.1025 m
3
s  kdsem .0
kdsem  11.8
0  8.854187187.1012 F.m
1
Ks
R0
2
2
 rc
2
lnrc   lnR0  1
2
  Vfb  Vgs  Kox R0  rc
2
R0
rc é a variável livre que se quer
encontrar e os demais parâmetros
são constantes conhecidas
do problema.
R0  100 Å
Vfb  1.12 V
0  Vgs  2 V
A equação que se quer resolver é:
onde
10

11. Para encontrarmos as raízes de uma equação
transcendental como a apresentada, no Maple,
vamos primeiramente escrevê-la como uma função
do tipo:
Ks
R0
2
2
 rc
2
lnrc   lnR0  1
2
  Vfb  Vgs  Kox R0  rc
2
R0
Jrc   Ks
R0
2
2
 rc
2
lnrc   lnR0  1
2
  Vfb  Vgs  Kox R0  rc
2
R0
11

12. Passando todos os termos para um lado
e nomeando-a, por exemplo, por J,
Jrc   Ks
R0
2
2
 rc
2
lnrc   lnR0  1
2
  Vfb  Vgs  Kox R0  rc
2
R0
12

13. Como desejamos encontrar as raízes dessa equação
(os zeros de função), primeiramente, vamos graficá-
la no Maple para entender o comportamento da
função em termos da variável de interesse, rc.
Jrc   Ks
R0
2
2
 rc
2
lnrc   lnR0  1
2
  Vfb  Vgs  Kox R0  rc
2
R0
13

14. O gráfico desta função no Maple resulta
no intervalo
Jrc   Ks
R0
2
2
 rc
2
lnrc   lnR0  1
2
  Vfb  Vgs  Kox R0  rc
2
R0
0  R0  100 Å
e revela uma
raiz real próximo
à 10 Å.
14
c

15. Mas, esta não é a única raiz real desta equação.
Jrc   Ks
R0
2
2
 rc
2
lnrc   lnR0  1
2
  Vfb  Vgs  Kox R0  rc
2
R0
15
c

16. Jrc   Ks
R0
2
2
 rc
2
lnrc   lnR0  1
2
  Vfb  Vgs  Kox R0  rc
2
R0
Se
procurarmos
num intervalo
maior, por
exemplo
0  R0  320 Å
16
c

17. Jrc   Ks
R0
2
2
 rc
2
lnrc   lnR0  1
2
  Vfb  Vgs  Kox R0  rc
2
R0
Veremos que
existem duas
raízes neste
intervalo.
17

18. Por exemplo, se rc representa pra você o raio de um
círculo na seção reta de um cilindro,
rc
18

19. Então o intervalo em que a raiz, rc, deve se
encontrar, tem que ser entre 0 e o raio do cilindro, R0.
rc
R0
19

20. No caso em que estamos considerando, R0=100 Å,
logicamente, que, a segunda raiz, rc próximo a 300 Å
não faz nenhum significado físico.
rc
R0
20

21. O intervalo esperado é algo entre 0 e 100 Å, de
modo que, não precisamos encontrar a segunda
raiz, pois não faz sentido em nosso problema
particular.
rc
R0
0  R0  100 Å
21

22. Atualmente dispomos de muitas ferramentas
matemáticas para realizar este tipo de trabalho,
sem termos necessidade de lançar mão de métodos
de cálculo numérico mais laboriosos.
22

23. Uma
ferramenta
bastante
interessante
para se fazer
isso é o
Maple.
23

24. No Maple
podemos recorrer
ao comando
fsolve
>
>
24

25. Sendo necessário
fornecer o intervalo
no qual a raiz que
você esta
buscando se
encontra.
fsolve
>
>
25

26. Se não, ele pode
fornecer apenas a
primeira raiz que
encontrar.
fsolve
>
26

27. Outra possibilidade
no Maple, é usar o
pacote
E o comando
>
>
Plano imaginário
27

28. Para finalizar o nosso estudo de hoje, vamos analisar
atentamente os códigos e entender as vantagens
de se usar o pacote
e o comando
ao invés do comando
fsolve
28

29. Códigos
Maple

30. 30

31. 31

32. 32

33. 33

34. 34

35. 35

36. FIM
36