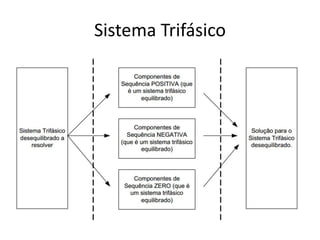
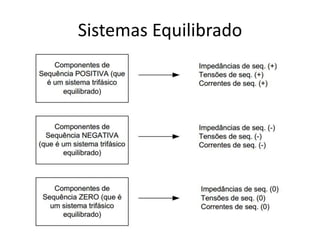
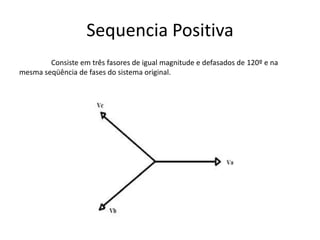
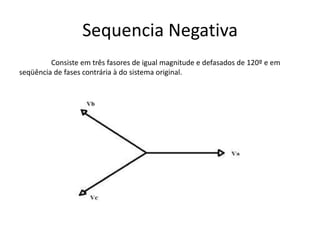
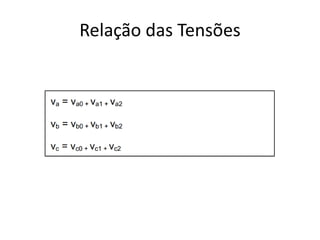
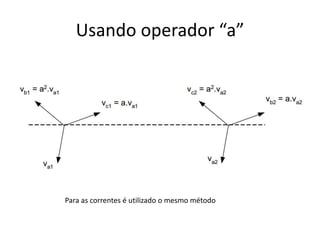
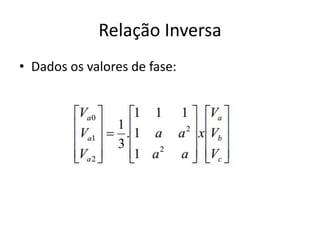
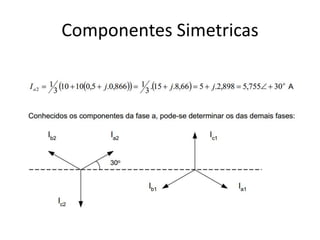
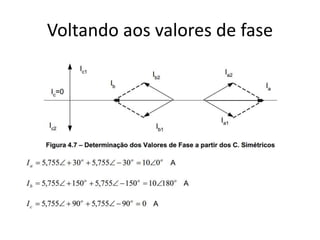
O documento descreve o Teorema de Fortescue, que estabelece que um sistema trifásico desequilibrado pode ser decomposto em três sistemas equilibrados chamados componentes simétricos. Estes componentes simétricos consistem nas sequências positiva, negativa e zero, que quando somadas reconstituem o sistema original desequilibrado. O documento também apresenta as relações entre as correntes e tensões dos componentes simétricos por meio de matrizes.

1. Circuitos Elétricos III
Componentes Simétricas

2. TEOREMA DE FORTESCUE

3. TEOREMA DE FORTESCUE
• Segundo o teorema de Fortescue:
Um sistema desequilibrado de n fasores
correlacionados pode ser decomposto em n
sistemas de fasores equilibrados denominados
componentes simétricos dos fasores originais.
Os n fasores de cada conjunto de componentes são
iguais em módulo e os ângulos entre fasores
adjacentes do conjunto são iguais".

4. TEOREMA DE FORTESCUE
Semelhante ao teorema de Fourier relativo a
ondas complexas, os componentes simétricos,
que é o teorema de Fortescue, consiste em
decompor um sistema trifásico não
equilibrado em três sistemas equilibrados, ou
seja, qualquer sistema de vetores trifásicos
não equilibrados pode ser resolvido com a
adição de três sistemas equilibrados.

5. Sistema Trifásico

6. Componentes Simétricas
Consistem de grandezas positivas, negativas
e de seqüência-zero:
seqüência-positiva - são aqueles presentes
durante condições trifásicas equilibradas.
seqüência-negativa - medem a quantidade de
desbalanço existente no sistema de potência e as
grandezas.
seqüência-zero - estão mais comumente
associadas ao fato de se envolver a terra em
condições de desbalanço.

7. Sistemas Equilibrado

8. Sequencia Positiva
Consiste em três fasores de igual magnitude e defasados de 120º e na
mesma seqüência de fases do sistema original.

9. Sequencia Negativa
Consiste em três fasores de igual magnitude e defasados de 120º e em
seqüência de fases contrária à do sistema original.

10. Sequencia Zero
Consiste em três fasores de iguais magnitude e fase angular.

11. Relação das Correntes

12. Relação das Tensões

13. Expressão Matricial

14. Multiplicação de Matrizes

15. Multiplicação de Matriz

16. Operadores Vetoriais

17. Usando operador “a”
Para as correntes é utilizado o mesmo método

18. Relação Inversa
• Dados os valores de fase:

19. Multiplicação de Matrizes

20. Exemplo

21. Resolvendo a Matriz

22. Componentes Simetricas

23. Demais fases

24. Voltando aos valores de fase

25. Conclusão