Baixado 178 vezes
Carregado porMichel Rodrigues
Componentes simétricas
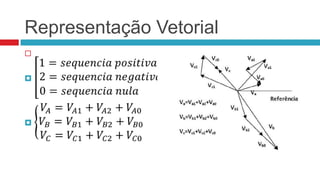
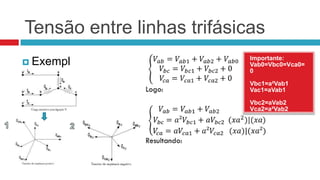
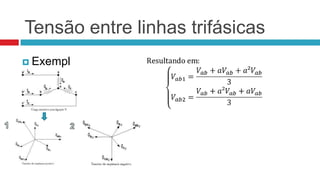
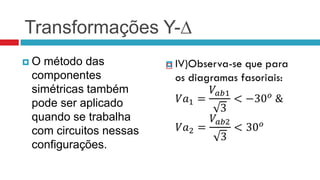
Este documento descreve o método das componentes simétricas para análise de sistemas trifásicos desequilibrados. Ele explica como decompor o sistema em três componentes equilibradas usando operadores de rotação e como calcular as componentes simétricas positiva, negativa e nula. Além disso, apresenta aplicações como tensão entre linhas, tensão de fase em Y, transformações Y-Δ, correntes trifásicas e potência.
Componentes simétricas
- 1. FERRAMENTAS DE AUXILIO DECÁLCULO: COMPONENTES SIMÉTRICAS UFC –Centro de Tecnologia -Departamento de Eng. Elétrica- Circuitos 2
- 2. O que são? Como funcionam? O sistema de mecanismos Consiste em decompor o simétricos foi criado para sistema trifásico desequilibrado em três facilitar a análise de equilibrados: circuitos analíticos de 1)Sist. Sequencia positiva componentes elétricos 2)Sist. Sequencia negativa desequilibrados. 3)Sist. Sequencia nula
- 3.
- 4. Serve para Esse operador é um “vetor unitário” relacionar qualquer adiantado de 120º da referência. sistema Desse modo, a² é um “vetor trifásico equilibrado unitário” adiantado 240º da referência. A função do operador aplicado a um vetor é apenas girá-lo.
- 5. A única Va1 diferença entre os vetores é o ângulo! Vb1
- 6. Cálculo das componentes simétricas Para podermos ter os valores do vetores das componentes simétricas é necessário manipular o sistema de equações dos vetores desequilibrados. Para se achar a primeira componente simétrica (Va1), basta multiplicar a segunda e terceira equação do sistema pelo operador a e a², respectivamente. O mesmo se aplica quando se deseja saber o valor segunda componente (Va2), contudo trocando a ordem das multiplicações. Para saber o valor da terceira componente (Va0), basta somar as equações
- 7. Cálculo das componentes simétricas Para podermos ter os valores do vetores das componentes simétricas é necessário manipular o sistema de equações dos vetores desequilibrados. Para se achar a primeira componente simétrica (Va1), basta multiplicar a segunda e terceira equação do sistema pelo operador a e a², respectivamente. O mesmo se aplica quando se deseja saber o valor segunda componente (Va2), contudo trocando a ordem das multiplicações. Para saber o valor da terceira componente (Va0), basta somar as equações
- 8. Cálculo das componentes simétricas Com as multiplicações realizadas, basta somar as três equações. Tendo em mente que (1+a+a²)=0 é possível continuar a simplificação.
- 9. Cálculo das componentes simétricas De modo semelhante aos passos realizados para encontrar Va1 ( componente de sequencia positiva), é possível encontrar as demais componentes facilmente, apenas atentando Importante: para as observações Lembre-se se realizar a explicitadas (invertendo a inversão para a multiplicação para a segunda componente componente negativa e (seq.negativa)! apenas somando para a
- 10. Ausência da componentesequencia nula Vale comentar que sempre que a soma dos vetores originais ( tensão ou corrente ) for zero, a condição de não existência da componente nula em questão ocorrerá.
- 11. Aplicações do métodode componentes simétricas • Tensão entre linhas trifásicas. • Correntes trifásicas de linha e • Tensão de fase de cargas em Y correntes de fase ∆ associado • Transformações Y-∆
- 12. Tensão entre linhastrifásicas Sabe-se que a soma das tensões eq. de linha é nula. O sistema pode ser representado por outros dois sistemas ( seq.positiva e seq.negativa) independente do tipo de ligação (Y ou ∆) Caso ∆, considera-se as tensões de fase Va,Vb &Vc como sendo aquelas de estrela correspondente.
- 13. Tensão entre linhastrifásicas Importante: Exempl Vab0=Vbc0=Vca0= 0 o: Vbc1=a²Vab1 Vac1=aVab1 Vbc2=aVab2 Vca2=a²Vab2
- 14. Tensão entre linhastrifásicas Exempl o:
- 15. Tensão de fasede cargas em Y Geralmente para sistemas não equilibrados a condição da soma das tensões de fase é diferente de zero. Assim essas tensões(fase) tem componentes de sequencia zero, mesmo que tais componentes não existam para o caso das tensões de linha
- 16. Transformações Y-∆ O métododas I)Converter impedancias de ∆ no Y equivalente componentes II)Determinar as simétricas também componentes simétricas pode ser aplicado de seq.positiva e negativa para as tensões de linha quando se trabalha III)Determinar as com circuitos nessas componentes simétricas configurações. de seq.positiva e negativa para as tensões de fase
- 17. Transformações Y-∆ O métododas componentes simétricas também pode ser aplicado quando se trabalha com circuitos nessas configurações.
- 18.
- 19. Correntes trifásicas delinha trifilar e correntes de fase ∆ associado Para esse caso não existe componente simétrica de sequencia nula. Importante: O método das componentes simétricas é funcional para qualquer vetor! (tensão,corrente,et c)
- 20. Correntes trifásicas delinha a 4 fios (neutro de retorno)
- 21. Correntes trifásicas delinha a 4 fios (neutro de retorno)
- 22. Potência • Potência por componentes simétricos. • Perdas por efeito Joule em função de componentes simétricas.
- 23.
- 24.
- 25. Perdas por efeitoJoule em função das componentes simétricas
- 26. Impedância • Componentes de sequencia positiva, negativa e nula de impedância. • Regra das sequencias aplicadas as tensões
- 27. Perdas por efeitoJoule em função das componentes simétricas
- 28. Perdas por efeitoJoule em função das componentes simétricas
- 29. Bibliografia: Componentes Simétricos –Prof. Mauro Guimarães, UFU –FEELT Disciplina de circuitos 2 ministrada pela prof.ª Ruth Leão Alunos: Amanda Freitas Araújo – matricula:0315181 Michel Ney de Almeida Barroso Rodrigues – matricula:0307729 Obrigado