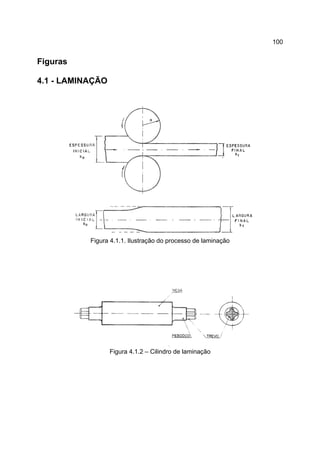
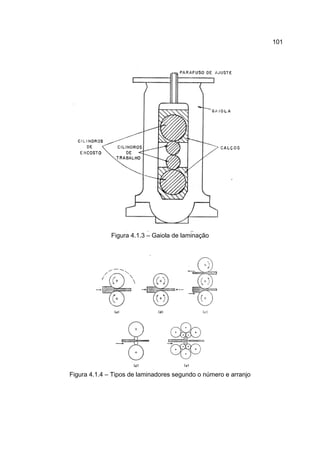
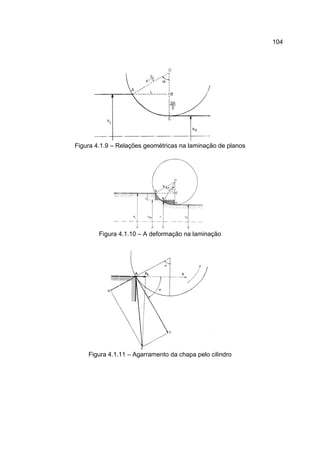
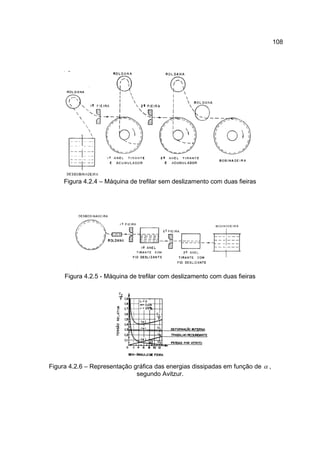
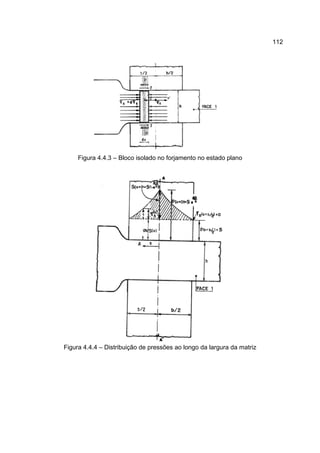
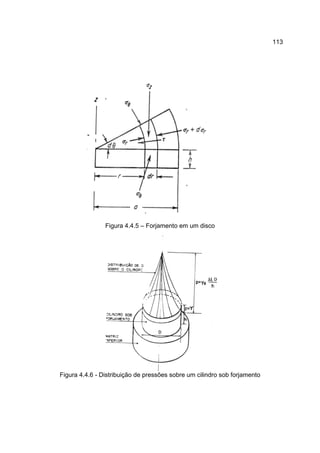
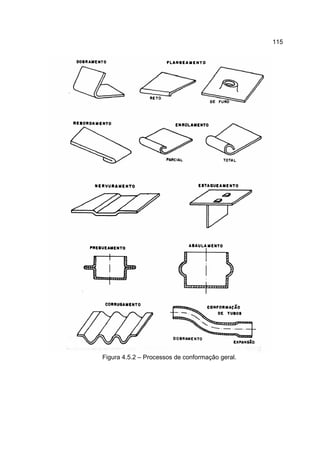
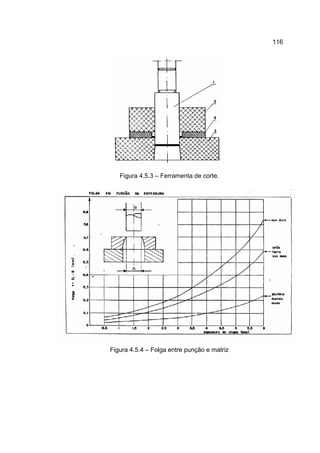
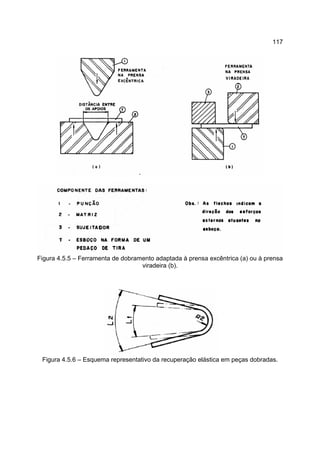
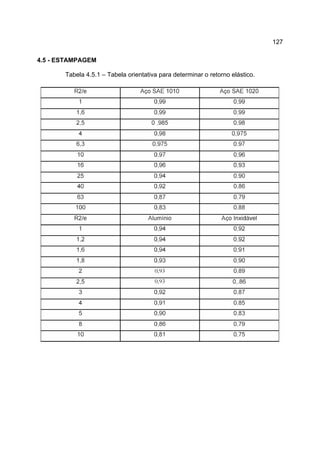
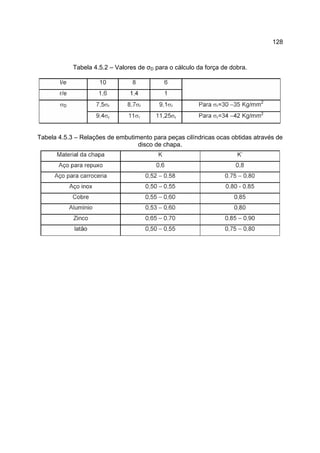
1) O documento descreve o processo de laminação, que envolve passar uma peça entre dois cilindros giratórios para reduzir sua espessura e aumentar sua largura e comprimento.
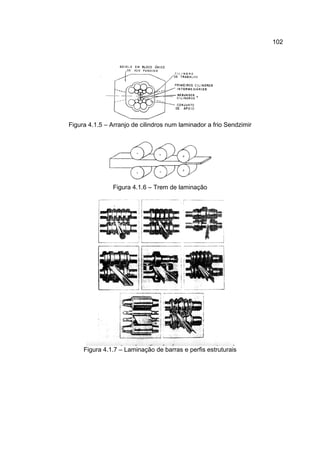
2) Existem diferentes tipos de laminadores classificados de acordo com o número e arranjo dos cilindros, como laminador duo, trio e quádruo.
3) A laminação pode ser realizada a quente ou a frio, dependendo das dimensões iniciais e finais desejadas para a peça.













![81
( )[ ]B
eT r
B
B
−−
+
= 11
1
σσ (4.2.11)
Levando em consideração o trabalho redundante φ , a equação (4.2.9) seria
corrigida sob a forma:
−
+
=
B
i
f
eT
D
D
B
B
2
1
1
σφσ (4.2.12)
Onde φ é dado pela equação (4.2.7)
4.2.2.4 – Equação de Avitzur
Avitzur obteve a seguinte equação para calcular a tensão de trefilação:
( )
⋅++−==
ff
ie
f
i
eT
R
L
m
R
R
gmg
senR
R
f lncot.cot
3
.2
ln.2. 2
αα
α
ασ
ασσ (4.2.13)
sendo: 0=L comprimento da zona cilíndrica
=m coeficiente de atrito
( )
−+⋅
+
+−−⋅=
αα
αα
α
α
2
2
2
12
11
1cos
12
11
12
11
1
ln.
12.11
1
12
11
1cos1
1
sen
sen
sen
f (4.2.14)
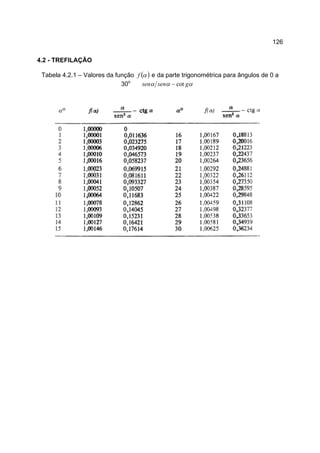
Os valores da função ( )αf para ângulos na faixa de 0 a 300
são apresentados
na Tabela 4.2.1.
Da equação (4.2.13):
1-A contribuição para a tensão total da deformação homogênea é levada em
consideração pelo termo:
( )
f
i
ei
R
R
fU ln2 σα= (4.2.15)
2-O efeito do atrito está considerado no termo:
f
i
ef
R
R
gmU lncot
3
2
ασ⋅= (4.2.16)](https://image.slidesharecdn.com/captulo4processosdeconformaoplstica-130508053916-phpapp01/85/Capitulo-4-processos-de-conformacao-plastica-14-320.jpg)