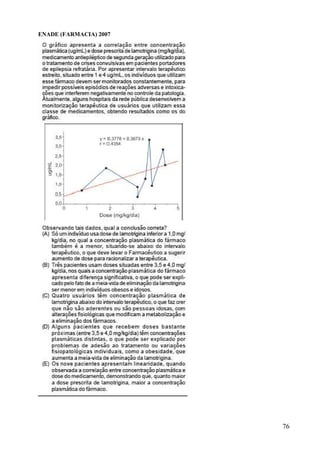
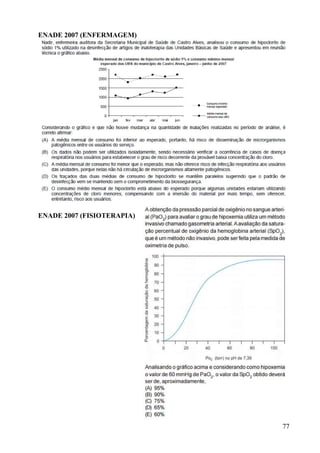
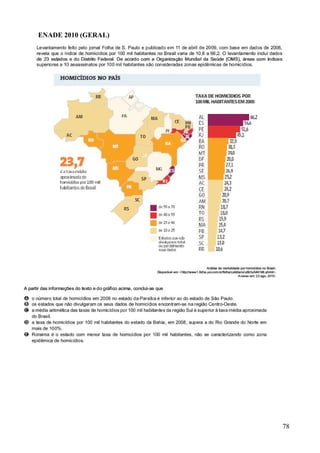
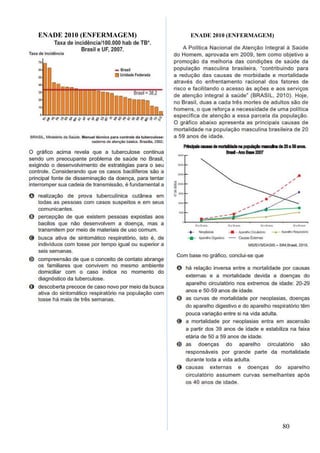
Este documento apresenta os principais conceitos de bioestatística, incluindo amostragem, organização de dados, medidas descritivas e correlação. Aborda temas como amostragem probabilística e não probabilística, distribuição de frequências, média, desvio padrão, moda, mediana e correlação linear. O objetivo é fornecer os fundamentos necessários para planejamento, coleta, avaliação e interpretação de dados em pesquisas na área da saúde.