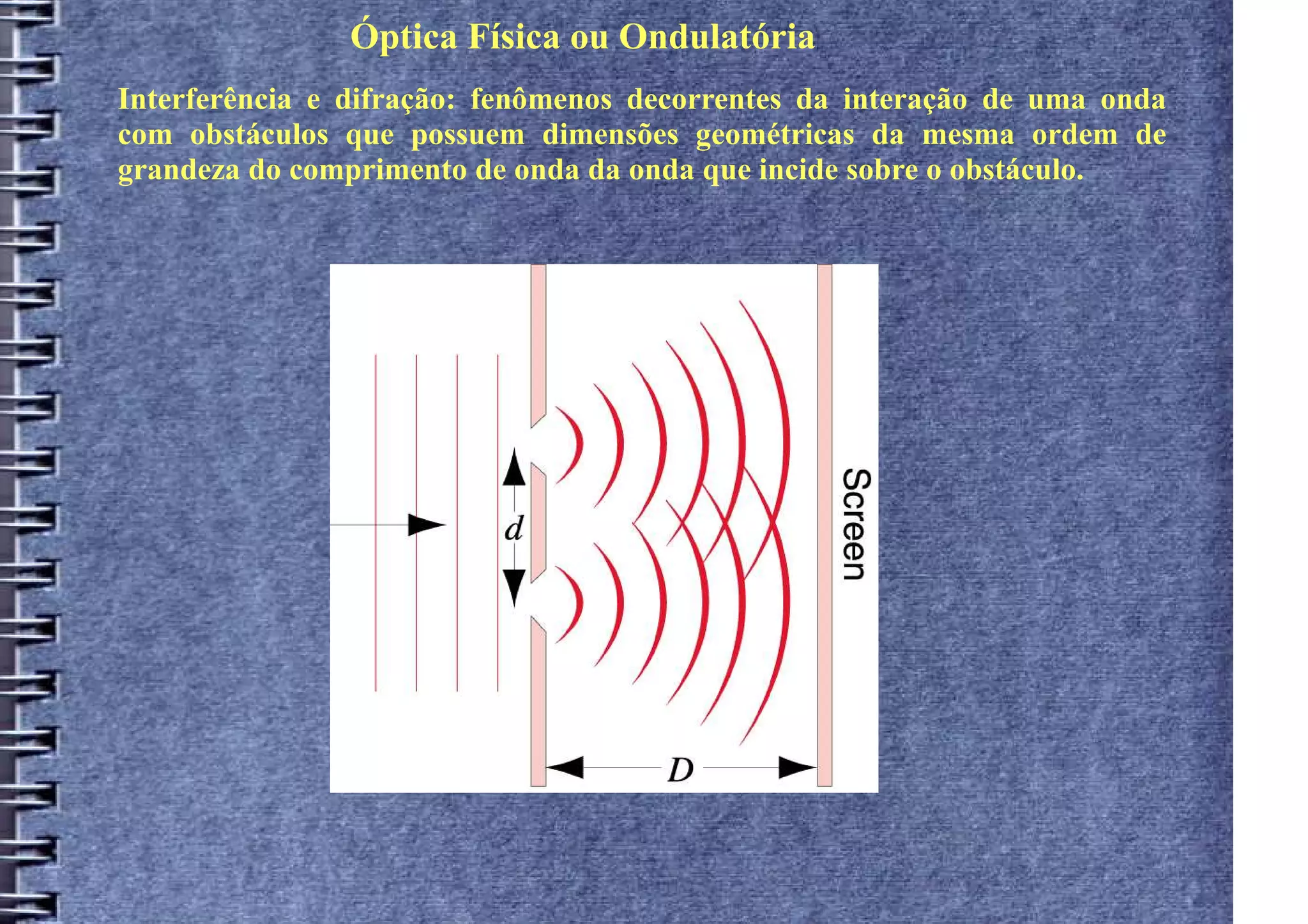
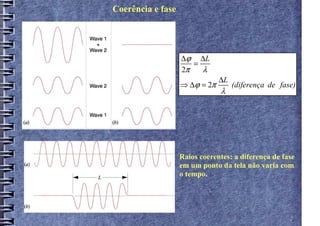
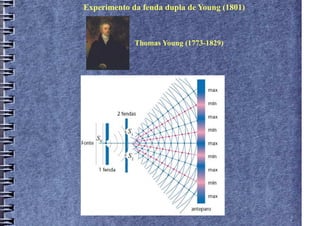
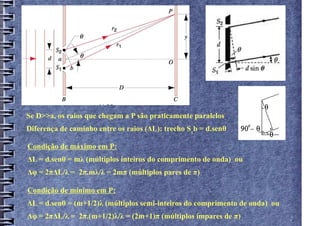
1) O documento discute interferência e difração, que ocorrem quando ondas interagem com obstáculos do tamanho da própria onda. 2) Explica a relação entre diferença de fase e diferença de caminho percorrido pela onda. 3) Descreve o experimento da fenda dupla de Young, usado para demonstrar a natureza ondulatória da luz.

1. Óptica Física ou Ondulatória
Interferência e difração: fenômenos decorrentes da interação de uma onda
com obstáculos que possuem dimensões geométricas da mesma ordem de
grandeza do comprimento de onda da onda que incide sobre o obstáculo.

2. Coerência e fase
∆ϕ ∆L
=
2π λ
∆L
⇒ ∆ϕ = 2π (diferença de fase)
λ
Raios coerentes: a diferença de fase
em um ponto da tela não varia com
o tempo.

3. Experimento da fenda dupla de Young (1801)
Thomas Young (1773-1829)

4. Se D>>a, os raios que chegam a P são praticamente paralelos
Diferença de caminho entre os raios (∆L): trecho S1b = d.senθ
Condição de máximo em P:
∆L = d.senθ = mλ (múltiplos inteiros do comprimento de onda) ou
∆φ = 2π∆L/λ = 2π.mλ/λ = 2mπ (múltiplos pares de π)
Condição de mínimo em P:
∆L = d.senθ = (m+1/2)λ (múltiplos semi-inteiros do comprimento de onda) ou
∆φ = 2π∆L/λ = 2π.(m+1/2)λ/λ = (2m+1)π (múltiplos ímpares de π)

5. Exercício Resolvido:
Iluminando a fenda dupla de Young com luz de λ = 546nm, qual a posição
angular do primeiro mínimo e do décimo máximo, considerando a separação
entre as fendas, d = 0,12mm e D = 55cm? Qual a distância y entre os máximos
adjacentes?
Primeiro mínimo :
 1 1
d .senθ =  m + λ ⇒ d .senθ = λ
 2 2
546 x10 −9
senθ = = 0,0023rad ⇒ θ = 0,0023rad (0,13o )
2.0,12 x10 −3
Décimo máximo :
d .senθ = mλ ⇒ d .senθ = 9λ
9.546 x10−9
senθ = = 0,04095rad ⇒ θ = 0,04095rad (2,4o )
0,12 x10−3
y mλ
senθ ≈ tgθ ≈ θ ⇒ tgθ = ≈ senθ =
D d
mλD mλD (m + 1)λD
y= ⇒ ym = ; ym +1 =
d d d
λD 546 x10 −9.0,55
∆y = ym +1 − ym = = = 2,5mm
d 0,12 x10 −3