1) Uma partícula está sujeita a uma força periódica representada por uma série de Fourier. Sua equação de movimento pode ser escrita como uma soma de senos com coeficientes determinados. 2) Um potencial anarmônico desloca o centro de oscilação de uma partícula para a direita com o aumento de energia. A força resultante aproxima-se de uma harmônica para pequenos deslocamentos. 3) A solução proposta para a equação de movimento não é exata. Desprezando termos de ordem

1. • 9a
Tarefa
1. Questão 12.63
Uma partícula de massa m está sujeita à força indicada na Fig.
12-52, denominada onda quadrática; isto é, a força tem módulo
constante, mas muda de sentido a intervalos de tempo regulares
de π
w
. Essa força pode ser representada pela série de Fourier:
F = F0(4/π)(sin wt +
1
3
sin 3wt +
1
5
sin 5wt...)
(a)Escreva a equação de movimento da partícula. (b) Verifique,
por substituição direta, que sua solução pode ser escrita como
x = a + bt + A sin wt + B sin 3wt + C sin 5wt...
onde a e b são constantes arbitrárias, e determine os valores dos
coeficientes A,B,C... de modo que a equação de movimento seja
satisfeita.
Resolução a) F = md2x
dt2
F
m
= 4F0/(πm)(sen(wt) + 1/3sen(3wt) + ...) =
d2
x
dt2
1

2. b)
dx
dt
= b + w(Acos(wt) + 3Bcos(3wt) + 5Ccos(5wt) + ...)
d2
x
dt2
= −w2
(Asen(wt) + 9Bsen(3wt) + 25Csen(wt)...)
4F0
(πm)(sen(wt) + 1/3sen(3wt) + ...)
=
d2
x
dt2
= −w2
(Asen(wt)+9Bsen(3wt)+25Csen(w
Igualando os dois lados da identidade:
A = −4F0
(πmw2)
B = −4F0
(27πmw2)
C = −4F0
(625πmw2)
...
Logo, x = [(somatório) A(indice i) sen(iwt)] + a + bt é solu-
ção da EDO, onde A(indice i) = −4F0
i3πmw2
2. Questão 12.67
Considere uma partícula oscilando sob a influência do potencial
anarmônico Ep(x) = 1
2
kx2
−zfrac13ax3
, onde a é positivo e muito
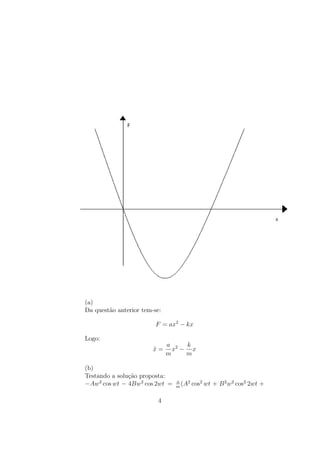
menor que k. (a) Faça um gráfico esquemático de Ep(x). A curva
é simétrica em torno do valor x = 0? Em vista da resposta que
você deu à pergunta anterior, em que sentido se desloca o centro
de oscilação quando a energia é aumentada? Você acha que xmed
deve ser nulo? (b) Obtenha a força como função de x e faça um
gráfico esquemático. Qual é o efeito do termo anarmônicosobre a
força?
Resolução
(a)
A curva não é simétrica em relação a x=0.
Em situações de baixa energia o movimento se assemelha a um
MHS, oscilando em torno de x = 0, porém, com o aumento da ener-
gia o centro se desloca para a direita visto que o termo anarmônico
faz com que os pontos com x>0 tenha menor energia do que seus
opostos.
Como o movimento não está centrado na origem xmed não é igual
2

3. a zero.
(b)
A força pode ser determinada como o oposto da derivada da ener-
gia em relação à distância x.
Logo:
F = ax2
− kx
Para valores pequenos de x a função se aproxima da equação do
MHS, pois k»a, para valores pequenos de x ax2
− kx ≈ −kx, mas
quando x aumenta o termo anarmônico deforma o movimento,
causando o efeito de deslocar o centro de oscilação observado no
item anterior.
3. Questão 12.68
Com relação ao problema precedente, (a) escreva a equação de
movimento. (b) Tente como solução
x = A cos wt + B cos 2wt + x1
, Onde os dois últimos termos resultam do termo anarmônico. (c)
Essa expressão pode representar uma solução exata? (d) Des-
prezando todos os termos que envolvem produtos de A e B ou
potência de B de ordem maior que a primeira, prove que w = w0,
x1 = αA2
/2w2
0 e B = −αA2
/6w2
0.
Resolução
3

4. (a)
Da questão anterior tem-se:
F = ax2
− kx
Logo:
¨x =
a
m
x2
−
k
m
x
(b)
Testando a solução proposta:
−Aw2
cos wt − 4Bw2
cos 2wt = a
m
(A2
cos2
wt + B2
w2
cos2
2wt +
4

5. x1
2
+2(Ax1 cos wt+Bx1 cos 2wt+AB cos wt cos 2wt))− k
m
(A cos wt+
B cos 2wt + x1)
(c)
Percebe-se que essa solução não pode ser exata, ou seja, a igual-
dade é falsa. Isso pode ser obsevado pois em um dos lados há um
produto cos wt cos 2wt que não é LD com cos wte cos 2wt.
(d)
Com as considerações do enunciado:
¨x = −Aw2
cos wt − 4Bw2
cos 2wt
x2
= A2
cos2
wt + x1
2
+ 2(Ax1 cos wt + Bx1 cos 2wt)
Sabe-se que ¨x − αx2
+
√
w0x = 0 Logo:
−Aw2
cos wt−4Bw2
(2 cos2
wt−1)−α(A2
cos2
wt+x1
2
+2(Ax1 cos wt+
Bx1(2cos2
wt − 1))) +
√
w0(A cos wt + B(2 cos2
wt − 1) + x1) = 0
Essa é uma equação do segundo grau em cos wt, igualando cada
coeficiente a zero e resolvendo o sistema obtém-se as relações de-
sejadas.
5