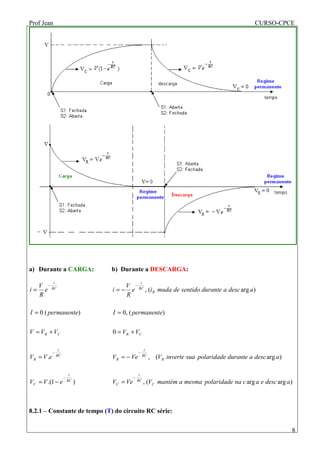
A) O documento discute análise de circuitos elétricos no regime transitório, quando uma chave é aberta ou fechada. Isso provoca mudanças na corrente e tensão. B) Nos circuitos RL série e RC série, a corrente e tensão mudam exponencialmente com o tempo segundo constantes de tempo características de cada circuito. C) Exemplos ilustram como calcular corrente e tensão nos regimes transitório e permanente para circuitos RL e RC.

1. Prof Jean CURSO-CPCE
1
ELETRICIDADE
AULA 8
ANÁLISE DE CIRCUITOS CHAVEADOS EM REGIME TRANSITÓRIO
PARA CORRENTE CONTÍNUA
Prof.: Jean
WWW.escoladoeletrotecnico.com.br
11 de julho de 2007
CURSO PREPARATÓRIO PARA CONCURSOS EM
ELETROTÉCNICA – CPCE

2. Prof Jean CURSO-CPCE
2
8 – Análise de circuitos no regime TRANSITÓRIO
Os circuitos com análise no regime transitório são circuitos que contém uma chave com a qual
é provocada esse regime seja, ao fechá-la ou ao abrí-la.
Quando inicialmente, o indutor e o capacitor estão SEM ENERGIA, no instante da comutação
da chave (fechar ou abrir), o indutor funciona como uma chave ABERTA e o capacitor como
uma chave FECHADA.
t = 0- : Instante de tempo antes de fechar ou abrir a chave
t = 0: Instante de tempo em que a chave é fechada ou aberta
t = 0+ : Instante de tempo depois de fechar ou abrir a chave
a) Circuito RLC série
Exercício1: Calcule a corrente I instante após fechar a chave. Considere o indutor e o
capacitor desenergizados no instante t =0.
Solução:
Como nenhuma corrente fluía pelo indutor antes, ao fechar a chave, ele vira uma chave
aberta. No caso do capacitor, ele vira uma chave fechada já que não tinha nenhuma
tensão nele antes do fechamento da chave.
I = 0 A
OBS: Ao comutar uma chave (fechando-a ou abrindo-a) passando do regime permanente
para o regime transitório, o
• INDUTOR mantém a MESMA CORRENTE do regime permanente, logo após a
comutação da chave.
• CAPACITOR mantém a MESMA TENSÃO do regime permanente, logo após a
comutação da chave.

3. Prof Jean CURSO-CPCE
3
b) Circuito RLC paralelo
Exercício 1: Calcule a corrente I instante logo após o fechamento da chave. Considere
o indutor e o capacitor desenergizados no instante t =0.
Solução:
AI 20
1
20
== ; RT = 1 Ω
c) Circuito misto
Exercício 1: Após um período de tempo em regime permanente, a chave K é aberta e nesta
condição, pede-se: o valor da corrente I.
Solução:
• No regime permanente, tínhamos o circuito abaixo:
mAA
k
I 610.6
2
12 3
=== −

4. Prof Jean CURSO-CPCE
4
• No regime transitório, logo após a abertura da chave temos o seguinte circuito:
mAA
k
I 210.2
6
12 3
=== −
EXERCÍCIOS
1)
Calcule a corrente I e a queda de tensão sobre o resistor de 3Ω após o fechamento da chave
considere o capacitor descarregado antes da comutação da chave.
Resposta: I = 9A; V = 0V
2)
No circuito da figura acima, inicialmente, o indutor e o capacitor se encontram desenergizados.
Após fechar a chave, calcule as correntes I1, I2 e IT.
Resposta I1 = 5A; I2 = 0A; IT = 5A,
3)
Na figura acima, após um longo período de tempo na posição 1, a chave S é comutada para a
posição 2. Pede-se: o valor da corrente I logo após comutar a chave e muito tempo depois.

5. Prof Jean CURSO-CPCE
5
Resposta Logo:I = 0A; Muito tempo depois, I = 0A ,
4)
No circuito da figura acima, inicialmente, não há energia no capacitor e no indutor no instante
em que a chave fecha (t = 0). Calcule os valores de I nos dois regimes (transitório e
permanente) após o fechamento da chave.
Resposta Transitório:I = 4mA; Permanente: I = 3mA
5)
Calcule a corrente I nos regimes transitório e permanente. Considere o indutor desenergizado
antes do fechamento da chave.
Resposta Transitório:I = 3A; Permanente: I = 4A
6)
Considere os capacitores e o indutor do circuito acima completamente descarregados, quando
em t = 0 a chave é fechada. Calcule o valor da corrente fornecida pela fonte logo após o
fechamento da chave e muito tempo depois.
Resposta Transitório:I = 2A; Muito tempo depois: I = 2/3A

6. Prof Jean CURSO-CPCE
6
8.1 – Forma de onda do circuito RL série
a) Durante a CARGA: b) Durante a DESCARGA
)(,
)1.(
.
)1.(
permanente
R
V
I
e
R
V
i
eVV
eVV
VVV
t
L
R
t
L
R
L
t
L
R
R
LR
=
−=
=
−=
+=
−
−
−
)arg(,.
.
0
)(0
)argarg(,.
adescadurantepolaridadesuainverteVeVV
eVV
VV
permanenteregimeI
adesceacnasentidomesmoomantémie
R
V
i
L
t
L
R
L
t
L
R
R
LR
t
L
R
−
−
−
−=
=
+=
=
=

7. Prof Jean CURSO-CPCE
7
Dicas:
•
t
L
R
e
−
= 1, para t = 0, (regime transitório)
•
t
L
R
e
−
= 0, para t = grande, (regime permanente)
8.1.1 – Constante de tempo (T) no circuito RL série:
:
R
L
T = Uma constante de tempo
:.2
R
L
T = duas constantes de tempo, assim por diante
Para t = T, %8,36368,01
.
==== −
−−
eee R
L
L
R
t
L
R
Isso quer dizer que: Na descarga, em uma constante de tempo (1T), a corrente cai para 36,8%
do seu valor do estado permanente I = V/R.
Os termos com: 1 -
t
L
R
e
−
= 0,632 = 63,2%, isso quer dizer que i ou VR atingem 63,2% do seu
valor do estado permanente após 1T.
8.2- Forma de onda de um circuito RC série

8. Prof Jean CURSO-CPCE
8
a) Durante a CARGA: b) Durante a DESCARGA:
)1.(
.
)(0
RC
t
C
RC
t
R
CR
RC
t
eVV
eVV
VVV
permanenteI
e
R
V
i
−
−
−
−=
=
+=
=
=
)argarg(,
)arg(,
0
)(,0
)arg(,
adesceacnapolaridademesmaamantémVVeV
adescadurantepolaridadesuainverteVVeV
VV
permanenteI
adescadurantesentidodemudaie
R
V
i
C
RC
t
C
R
RC
t
R
CR
R
RC
t
−
−
−
=
−=
+=
=
−=
8.2.1 – Constante de tempo (T) do circuito RC série:

9. Prof Jean CURSO-CPCE
9
T = RC
Para t = T, %8,36368,01
==== −
−−
eee RC
RC
RC
t
Dicas:
• RC
t
e
−
= 1, para t = 0, (regime transitório)
• RC
t
e
−
= 0, para t grande, (regime permanente)
Obs:
• Tanto para um circuito RL série como para um RC série, o regime permanente é alcançado
após cinco constantes de tempo, (t = 5T).
• O regime transitório é também chamado de estado transitório e o regime permanente
de estado permanente.
RESUMO:___________________________________________________________________
A) Circuito RL série
• CARGA
Regime transitório, t = 0 => e- Rt/L
= 1:
VR = 0 V VL = V i = 0 A
Regime permanente, t > 5T => e- Rt/L
= 0:
VR = V VL = 0 V I = V/R
• DESCARGA
Regime transitório, t = 0 => e- Rt/L
= 1:
VR = V VL = - V i = V/R
Regime permanente, t > 5T => e- Rt/L
= 0:
VR = 0 V VL = 0 V I = 0 A
• CONSTANTE DE TEMPO (T):
T = L/R

10. Prof Jean CURSO-CPCE
10
Exemplo: Para t = T,
R
V
i .368,0= (descarga)
B) Circuito RC série
• CARGA
Regime transitório, t = 0 => e- t/(RC)
= 1:
VR = V VC = 0 V i = V/R
Regime permanente, t > 5T => e- t/(RC)
= 0:
VR = 0 V VC = V I = 0 A
• DESCARGA
Regime transitório, t = 0 => e- t/(RC)
= 1:
VR = - V/R VC = V i = - V/R
Regime permanente, t > 5T => e- t/(RC)
= 0:
VR = 0 V VC = 0 V I = 0 A
• CONSTANTE DE TEMPO (T):
T = RC
Exemplo 1:
Deseja-se carregar o capacitor da figura abaixo que inicialmente, estava completamente
descarregado. Pede-se o valor da tensão no capacitor em t = T e t = 5T.
Solução:
Na carga, a tensão no capacitor é dada como: )1.()( RC
t
C eVtV
−
−=
• Para t =T = RC, a expressão )1( RC
t
e
−
− = 0,632. Logo,

11. Prof Jean CURSO-CPCE
11
VTtVC 58,7632,0.12)( ===
• Para t = 5T, o capacitor já se carregou totalmente. Sendo assim, RC
t
e
−
= 0 e
VTtVC 12)01.(12)5( =−== , ou seja, o capacitor entrou no regime permanente e abriu-se.
Exemplo 2: Depois de carregar o capacitor do exemplo 1 com uma tensão de 12V, deseja-se
descarregá-lo. Pede-se para calcular a tensão no capacitor em t = T e t= 5T após o fechamento da
chave S.
Solução:
Na descarga a tensão no capacitor é dada como: RC
t
C eVtV
−
= .)(
• Para t = T = RC, a expressão RC
t
e
−
= 0,368. Logo,
VTtVC 42,4368,0.12)( ===
• Para t = 5T, o capacitor pode ser considerado totalmente descarregado. Sendo assim, RC
t
e
−
≈ 0
e VTtVC 00.12)5( ===
Obs.: A mesma analogia pode ser feita em relação ao circuito RL, estudando, neste caso, a corrente.

12. Prof Jean CURSO-CPCE
12