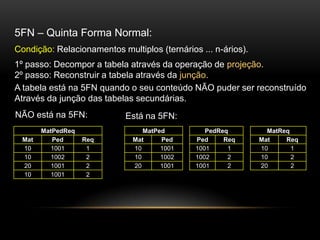
O documento discute os conceitos e objetivos da normalização de banco de dados, apresentando as primeiras cinco formas normais (1FN a 5FN). Resume as condições e exemplos para cada forma normal, mostrando como decompor tabelas para alcançar cada nível de normalização.

1. NORMALIZAÇÃO

2. NORMALIZAÇÃO
• Conceito introduzido em 1970 por E. F. Codd (1FN)
• Processo matemático formal fundamentado na
teoria dos conjuntos
• Aplica uma série de regras sobre as tabelas de um
banco de dados para verificar se estas foram
corretamente projetadas

3. OBJETIVOS PRINCIPAIS
• Garantir a integridade dos dados, evitando que
informações sem sentido sejam inseridas
• Organizar e dividir as tabelas da forma mais
eficiente possível, diminuindo a redundância e
permitindo a evolução do banco de dados

4. FORMAS NORMAIS:
• 1FN – 1ª Forma Normal
• 2FN – 2ª Forma Normal
• 3FN – 3ª Forma Normal
• FNBC – Forma Normal de Boyce e Codd
• 4FN – 4ª Forma Normal
• 5FN – 5ª Forma Normal

5. 1FN – Primeira Forma Normal:
Os atributos da tabela não contêm grupos de repetição (tabelas aninhadas).
A tabela a seguir NÃO está na 1FN:
Projeto
CodProj DescProj CodFunc NomeFunc CargoFunc SalFunc DtInicio
1001 Antonio Analista Sr 1800 02/01/2005
11 Alfa
1004 Daniela Analista Pl 1200 05/01/2005
12 Beta 1003 Claudio Analista Sr 1800 10/02/2005
Passando para a 1FN:
ProjFunc Projeto
CodProj CodFunc NomeFunc CargoFunc SalFunc DtInicio CodProj DescProj
11 1001 Antonio Analista Sr 1800 02/01/2005 11 Alfa
11 1004 Daniela Analista Pl 1200 05/01/2005 12 Beta
12 1003 Claudio Analista Sr 1800 10/02/2005

6. 2FN – Segunda Forma Normal:
Condição: Chave Primária (PK) composta por mais de uma coluna.
Todas as colunas que não fazem parte da PK dependem de todas as
colunas que compõem a PK.
A tabela a seguir NÃO está na 2FN:
ProjFunc
CodProj CodFunc NomeFunc CargoFunc SalFunc DtInicio
11 1001 Antonio Analista Sr 1800 02/01/2005
11 1004 Daniela Analista Pl 1200 05/01/2005
12 1003 Claudio Analista Sr 1800 10/02/2005
Passando para a 2FN:
Funcionario ProjFunc
CodFunc NomeFunc CargoFunc SalFunc CodProj CodFunc DtInicio
1001 Antonio Analista Sr 1800 11 1001 02/01/2005
1004 Daniela Analista Pl 1200 11 1004 05/01/2005
1003 Claudio Analista Sr 1800 12 1003 10/02/2005

7. 3FN – Terceira Forma Normal:
Não há dependências funcionais transitivas.
Cada coluna não PK depende DIRETAMENTE da PK.
A tabela a seguir NÃO está na 3FN:
Funcionario
CodFunc NomeFunc CargoFunc SalFunc CodFunc  CargoFunc  SalFunc
1001 Antonio Analista Sr 1800
1004 Daniela Analista Pl 1200
1003 Claudio Analista Sr 1800 Dependência Funcional Transitiva
Passando para a 3FN:
Funcionario CargoSalario
CodFunc NomeFunc CargoFunc CargoFunc SalFunc
1001 Antonio Analista Sr Analista Sr 1800
1004 Daniela Analista Pl Analista Pl 1200
1003 Claudio Analista Sr

8. FNBC – F N Boyce e Codd:
Condição: Aplica-se a FNBC quando:
1. Encontramos duas ou mais chaves candidatas
2. As chaves candidatas apresentam mais de um atributo (são compostas)
3. Todas as chaves candidatas têm um atributo em comum
Exemplo:
Vamos assumir que um professor está associado a mais de uma escola e uma sala.
Aluno(NomeAluno,EndAluno,NomeEscola,NrSala,NomeProf)
Chaves Candidatas: Neste exemplo:
NomeAluno + EndAluno 1. Encontramos três chaves candidatas
NomeAluno + NrSala 2. Todas são compostas
NomeAluno + NomeProf 3. Todas compartilham um mesmo atributo
Aplicando a FNBC: A tabela Aluno será dividida em duas tabelas: uma que contêm
todos os atributos que descrevem o aluno e outra que contêm os atributos que
designam um professor em uma determinada escola e número de sala.
Aluno(NomeAluno,EndAluno,NomeEscola,NrSala)
Professor(NomeEscola,NrSala,NomeProf)

9. 4FN – Quarta Forma Normal:
Uma tabela não deve possuir mais de uma dependência multivalorada.
A tabela a seguir NÃO está na 4FN:
ProjFuncEquip
CodProj CodFunc CodEquip
11 1001 A10
11 1002 A10 CodProj  CodFunc
11 1001 A20
11 1002 A20
CodProj  CodEquip
12 1001 A10
12 1001 A20
Passando para a 4FN:
ProjFunc ProjEquip
CodProj CodFunc CodProj CodEquip
11 1001 11 A10
11 1002 11 A20
12 1001 12 A10
12 A20

10. 5FN – Quinta Forma Normal:
Condição: Relacionamentos multiplos (ternários ... n-ários).
1º passo: Decompor a tabela através da operação de projeção.
2º passo: Reconstruir a tabela através da junção.
A tabela está na 5FN quando o seu conteúdo NÃO puder ser reconstruído
Através da junção das tabelas secundárias.
NÃO está na 5FN: Está na 5FN:
MatPedReq MatPed PedReq MatReq
Mat Ped Req Mat Ped Ped Req Mat Req
10 1001 1 10 1001 1001 1 10 1
10 1002 2 10 1002 1002 2 10 2
20 1001 2 20 1001 1001 2 20 2
10 1001 2