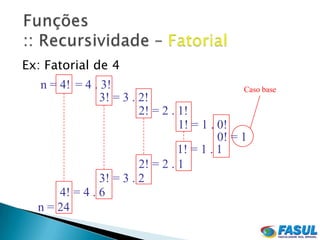
O documento discute recursividade, definindo-a como um objeto ou processo que se refere a si mesmo. Explica que recursividade divide um problema em subproblemas da mesma natureza e fornece exemplos como fatorial e fibonacci. Também discute vantagens e desvantagens de programação recursiva.

1. Recursividade
Prof. Adriano Teixeira de Souza

2.  Um objeto é dito recursivo se pode ser
definido em termos de si próprio.
“Para fazer iogurte, você precisa de
leite e de um pouco de iogurte.”
“Para entender recursividade, você
primeiro tem de entender
recursividade.”
Prof. Adriano Teixeira de Souza

3.  A recursão é uma forma interessante de resolver
problemas, pois o divide em problemas menores
de mesma natureza.
 Um processo recursivo consiste de duas partes:
◦ O caso trivial, cuja solução é conhecida.
◦ Um método geral que reduz o problema a um ou mais
problemas menores de mesma natureza.
Prof. Adriano Teixeira de Souza

4.  Um programa recursivo é um programa que chama
a si mesmo, direta ou indiretamente.
 Vantagens
◦ Redução do tamanho do código fonte
◦ Permite descrever algoritmos de forma mais clara e Concisa
 Desvantagens
◦ Redução do desempenho de execução devido ao tempo
para gerenciamento de chamadas
◦ Dificuldades na depuração de programas
recursivos, especialmente se a recursão for muito
profunda
Prof. Adriano Teixeira de Souza

5.  Cada vez que uma função é chamada de forma
recursiva, é alojado e guardado uma cópia dos
seus parâmetros por forma a não perder os valores
dos parâmetros das chamadas anteriores.
 Em cada instância da função, só são diretamente
acessíveis os parâmetros criados para esta
instância, não sendo directamente acessíveis os
parâmetros de outras instâncias.
Prof. Adriano Teixeira de Souza

6.  As funções recursivas contêm duas partes
fundamentais:
◦ Ponto de Parada: o ponto de parada da recursividade é
resolvido sem utilização de recursividade, sendo este ponto
geralmente um limite superior ou inferior da regra geral.
◦ Regra Geral: o método geral da recursividade reduz a
resolução do problema através da invocação recursiva de casos
mais pequenos, sendo estes casos mais pequenos resolvidos
através da resolução de casos ainda mais pequenos, e assim
sucessivamente, até atingir o ponto de parada que finaliza o
método.
Prof. Adriano Teixeira de Souza

7.  Cálculo do fatorial:
1, se n = 1
fat(n) =
n * fat(n-1), se n > 1
Prof. Adriano Teixeira de Souza

8.  Recursividade é a propriedade que uma função
tem de chamar a si própria, diretamente ou não.
Isto é usado para simplificar um problema. É um
caso particular de aninhamento.
Exemplo mais comum de recursão: função Fatorial
Caso base
0!=1
1!=1.0!=1 Regra Geral:
2!=2.1!=2.1 n ! = n * (n-1) !
3!=3.2!=3.2.1 fat(n) = n * fat(n-1)
4!=4.3!=4.3.2.1

9. Ex: Fatorial de 4
n = 4! = 4 . 3! Caso base
3! = 3 . 2!
2! = 2 . 1!
1! = 1 . 0!
0! = 1
1! = 1 . 1
2! = 2 . 1
3! = 3 . 2
4! = 4 . 6
n = 24

10.  Como fica o Fatorial de 5?
Prof. Adriano Teixeira de Souza

11.  Como uma função recursiva pode chamar a si
mesma indefinidamente, é essencial a existência
do caso base, ou condição de parada. No caso do
fatorial, o caso base é o zero, cujo valor do
fatorial é 1. A partir dele, são encontrados todos
os outros valores.
int fatorial(int n) {
if (n == 0) // caso base, onde a recursão acaba
return 1;
else // caso indutivo
return ( n * fatorial( n-1 ) );
}

12.  1) Exponenciação. Escreva uma função recursiva
eficiente que receba inteiros positivos k e n e
calcule k n. (Suponha que kn cabe em um int.)
Quantas multiplicações sua função executa
aproximadamente?
 2) Qual o valor de X (4)?
int X (int n) {
if (n == 1 || n == 2) return n;
else return X (n-1) + n * X (n-2);
}
Prof. Adriano Teixeira de Souza

13.  3) A sequência de Fibonacci é dada pela
seguinte fórmula:
 Apresente uma solução por meio de função
recursiva que calcule e imprima os números
da sequência até o i-ésimo termo.
Prof. Adriano Teixeira de Souza

14.  3) Implemente uma função recursiva soma(n)
que calcula o somatório dos n primeiros
números inteiros.
Prof. Adriano Teixeira de Souza