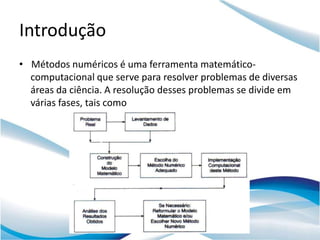
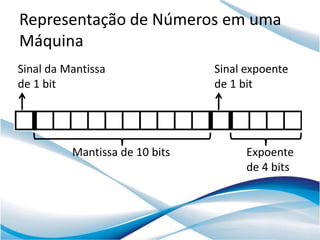
O documento discute representação numérica e erros em computadores. Ele explica como números são representados em binário, como converter entre bases numéricas, e como números reais são armazenados usando ponto flutuante. Ele também discute erros que podem ocorrer em operações numéricas devido à precisão finita de computadores.

1. Noções Básicas de Erros
Prof.: Samyr Jácome

2. Índice
• Introdução
• Representação de Números
• Conversão de Números nos Sistema Decimal e
Binário
• Representação de Números em uma Máquina
• Operações Aritméticas com Ponto Flutuante

3. Introdução
• Métodos numéricos é uma ferramenta matemático-
computacional que serve para resolver problemas de diversas
áreas da ciência. A resolução desses problemas se divide em
várias fases, tais como

4. Introdução
• Em geral, aos nos depararmos com resultados finais
provenientes de algum método numérico, é comum que estes
resultados não estejam de acordo com o resultados reais.
Frequentemente, estes resultados são próximos do esperado.
• Os resultados obtidos dependem:
– da precisão dos dados de entrada;
– da forma como esses resultados são representados no
computador;
– das operações numéricas efetuadas.
• Estudaremos aqui erros provenientes da representação de
números em um computador e os erros resultantes das
operações numéricas efetuadas.

5. Representação de Números
• Vamos analisar dois casos:
CASO 01: Calcular a área de um círculo de raio 100m.
RESULTADO 01:
a) Usando 3.14 , teremos A 31400m 2
b) Usando 3.1416 , teremos A 31416m 2
c) Usando 3.141592654 ,
teremos A 31415.92654m2
• Porque a diferença entre os resultados?

6. Representação de Números
CASO 02: Efetuar o somatório abaixo em uma calculadora e
em um computador
30000
S xi
i 1
para xi 0.5 e para xi 0.11
RESULTADO 02:
calculadora : S 15000
i) para xi 0.5
computador : S 15000
calculadora : S 3300
ii) para xi 0.11
computador : S 3299 .99691

7. Representação de Números
• Como justificar a diferença entre os resultados obtidos pela
calculadora e pelo computador para xi 0.11 ?
RESPOSTA: O erro ocorreu devido a representação numérica
no computador.
• A representação de um número depende da base escolhida
ou disponível na máquina em uso e do número de dígitos da
sua representação.
• Veremos mais adiante que um número pode ter
representação finita em uma base e
não-finita em outra.

8. Conversão de números nos sistemas
decimal e binário
• Consideremos os seguinte números de modo que possamos
reescrevê-los na forma:
(347 )10 3 10 2 4 10 1 7 10 0
(406 ,032 )10 4 10 2 0 10 1 6 10 0 0 10 1
3 10 2
2 10 3
(10111 ) 2 1 2 4 0 23 1 2 2 1 21 1 20
(10 ,11) 2 1 21 0 20 1 2 1
1 2 2
• Podemos concluir que um número em qualquer base pode ser
escrito na forma acima.

9. Conversão de números nos sistemas
decimal e binário
• Em geral, um número real N pode ser escrito numa base
qualquer na forma polinomial da seguinte forma
N (am ...a2 a1a0 a 1a 2 ...an )
m 2 1 0 1 2 n
N am ... a2 a1 a0 a 1 a 2 ... an
com (am ...a2 a1a0 a 1a 2 ...an ) , 0 ak e inteiros m 0
n 0
• É possível converter um número de uma base para outra e
vice-versa?

10. Conversão de números nos sistemas
decimal e binário
Converter número da base 2 para base 10:
• A partir da forma polinomial, um número na base 2 pode ser
escrito como
am 2 m ... a2 2 2 a1 21 a0 2 0 a 12 1
a 22 2
... an 2 n
com ai 0 ou 1
• Para mudar de base 2 para base 10, basta multiplicar o dígito
binário por uma potência de 2 apropriada e somá-los.
(10111) 2 1 2 4 0 23 1 2 2 1 21 1 20
16 0 4 2 1
(23)10

11. Conversão de números nos sistemas
decimal e binário
Converter número da base 2 para base 10:
(100,11) 2 1 2 2 0 21 0 20 1 2 1
1 2 2
4 0 0 0,5 0,25
(4,75)10
(101,01) 2 1 2 2 0 21 1 20 0 2 1
1 2 2
4 0 1 0 0,25
(5,25)10

12. Conversão de números nos sistemas
decimal e binário
Converter número da base 10 para base 2:
• Para converter da base 10 para base 2, aplica-se um processo
para parte inteira e outra para parte fracionária.
• Parte inteira: nesse caso usamos o método das divisões
sucessivas, que consiste em dividir o número por 2, a seguir
dividi-se o quociente encontrado por 2, e assim o processo é
repetido até que o último quociente seja igual a um. O
número binário será, então, formado pela concatenação do
último quociente com os restos das
divisões lidos no sentido inverso
aos que foram obtidos. (Ex. no quadro)

13. Conversão de números nos sistemas
decimal e binário
Converter número da base 10 para base 2:
• Parte fracionária: nesse caso usamos o método das
multiplicações sucessivas, que consiste em:
a) multiplicar a parte fracionária do número por 2;
b) deste resultado, a parte inteira será o primeiro dígito na
base dois e a parte fracionária é novamente multiplicada por
2. O processo é repetido até que a parte fracionária do último
produto seja igual a zero. Quando o produto da parte
fracionário nunca for zero, teremos uma
dízima infinita. (Ex. no quadro)

14. Representação de Números em uma
Máquina
• Internamente, um número é representado na máquina de
calcular ou num computador digital através de uma sequência
de impulsos elétricos que indicam dois estados: 0 ou 1, ou
seja, os números são representados na base 2 ou binária.
• Cada impulso elétrico é chamado de bit. Sendo assim, como
representar no computador um número fracionário se não
podemos, por exemplo, armazenar ½ bit ?
• Como fazer isso?

15. Representação de Números em uma
Máquina
• Vamos considerar um número real x em uma base qualquer
de modo que possamos reescrevê-lo como sendo uma soma
de frações, cujos denominadores são potências de mesma
base , vezes um fator elevado a um expoente.
Exemplos:
(347 )10 ?

16. Representação de Números em uma
Máquina
• Vamos considerar um número real x em uma base qualquer
de modo que possamos reescrevê-lo como sendo uma soma
de frações, cujos denominadores são potências de mesma
base , vezes um fator elevado a um expoente.
Exemplos:
(347)10 3 102 4 101 7 100
3 4 7
103
101 102 103

17. Representação de Números em uma
Máquina
(406 ,032 )10 ?
(10111 ) 2 ?
(10,11) 2 ?

18. Representação de Números em uma
Máquina
(406,032)10 4 102 0 101 6 100 0 10 1
3 10 2
2 10 3
4 0 6 0 3 2
103
101 102 103 104 105 106
(10111) 2 1 2 4 0 23 1 2 2 1 21 1 20
1 0 1 1 1
25 (23)10
21 22 23 24 25
(10,11) 2 1 21 0 20 1 2 1
1 2 2
1 0 1 1
22 2,75 10
21 22 23 24

19. Representação de Números em uma
Máquina
• Podemos concluir, portanto, que um número real x pode ser
genericamente representado em uma base qualquer por
d1 d2 d3 dt E
x 1 2 3
... t
onde
d1 d2 d3 dt
1 2 3
... t
é chamada de mantissa
di são números inteiros contidos no intervalo 0 d i 1
com i 1,2,3,...,t e d1 0
E é o expoente de

20. Representação de Números em uma
Máquina
• Podemos simplificar a notação de mantissa colocamos os
dígitos significativos entre < >, ou seja,
d1 d2 d3 dt E E
x 1 2 3
... t
d1d 2 d3 ...dt
desta forma teríamos, por exemplo,
(347 )10 347 10 3
(406 ,032 )10 406032 10 3
(10111 ) 2 10111 25 (23)10
(10 ,11) 2 1011 22 2,75 10

21. Representação de Números em uma
Máquina
• A forma acima definida é conhecida como forma de mantissa.
• A forma de mantissa é bastante importante do ponto de
vista computacional, pois é uma maneira eficaz de
eliminarmos a vírgula dos números com parte fracionária.
• A mantissa sempre resulta em um valor normalizado, ou seja,
entre 0 e 1, que representa os dígitos significativos e t é
quantidade de dígitos significativos do sistema de
representação, comumente chamado de precisão da máquina.

22. Representação de Números em uma
Máquina
• Quando aplicado a uma máquina binária, ou seja, máquina
com armazenamento e operações binárias, a representação
na forma de mantissa é conhecida como aritmética de ponto
flutuante e recebe algumas restrições devido a limitação da
própria máquina. São elas:
t quantidade máxima de dígitos significat ivos
E o expoente inteiro de que assume
valores entre S E S com S inteiro

23. Representação de Números em uma
Máquina
• Em uma máquina binária padrão, cada dígito é chamado de
bit e a representação dos números é estruturada da seguinte
maneira:
Um bit para o sinal da mantissa, onde bit = 0 se positivo e bit = 1
se negativo;
t bits para a mantissa;
Um bit para o sinal do expoente, onde bit = 0 se positivo e bit =
1 se negativo;
s bits (s é a quantidade de bits do maior expoente inteiro S na
forma binária).

24. Representação de Números em uma
Máquina
• Desta forma, em um computador com armazenamento de
32bits possui um bit para o sinal da mantissa, 23 bits para a
mantissa, um bit para o sinal do expoente e 7 bits para o valor
do expoente.
EX 01: Numa máquina de 16 bits de calcular, cujo sistema de
representação utilizado tenha =2, t = 10 e S = (15)10 . Como o
número 25 na base decimal é representado na máquina?
(Resposta no quadro)

25. Representação de Números em uma
Máquina
Sinal da Mantissa Sinal expoente
de 1 bit de 1 bit
Mantissa de 10 bits Expoente
de 4 bits

26. Representação de Números em uma
Máquina
EX 02: Utilizando a mesma máquina do exemplo
anterior, represente o número (3,5)10 .
EX 03: Utilizando a mesma máquina do exemplo
anterior, represente o número (-7,125)10 .
EX 04: Qual o maior e o menor valor em módulo
representado nessa máquina?
EX 05: Considerando que o número zero seria nessa máquina
quando todos os dígitos fossem iguais a zero, quais seriam os
dois primeiros números positivos?

27. Operações Aritméticas com Ponto
Flutuante
• A operação em aritmética com ponto flutuante requer o
alinhamento dos pontos decimais dos dois números. Para isso,
a mantissa do número de menor expoente deve se deslocada
para a direita. Esse deslocamento deve ser de um número de
casa decimais igual a diferença entre os dois expoentes.
2
Ex 01: Dados x 0.937 104 e y 0.1272 10 , obter x y .
Qual seria o resultado se essa operação fosse realizada em
uma máquina operasse com o número de dígitos significativos
igual t 4 . Qual seria o erro absoluto e relativo se no
arredondamento e truncamento?