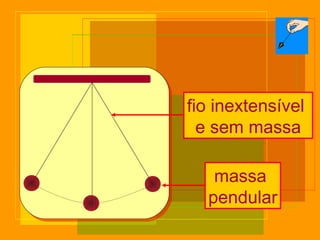
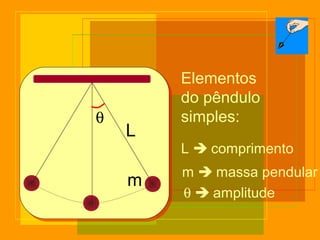
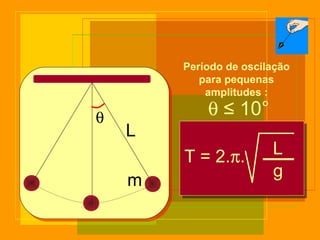
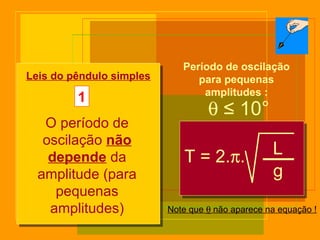
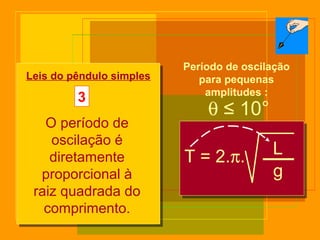
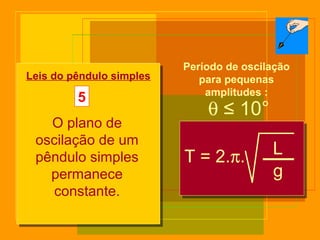
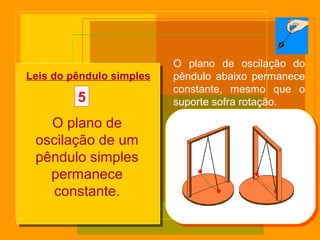
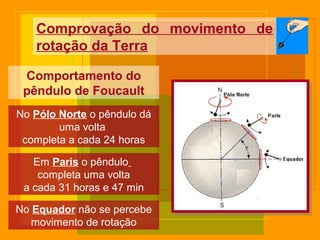
O documento descreve o pêndulo simples, incluindo sua definição, elementos, leis de movimento e principais aplicações. É apresentada a equação para o período de oscilação e explica como o pêndulo foi usado para comprovar o movimento de rotação da Terra e medir a aceleração da gravidade.

1. Física 1
Prof. Manika

2. Um pêndulo simples é um
sistema ideal que consiste de
uma partícula suspensa por um
fio inextensível e leve.
Quando afastado de sua
posição de equilíbrio e solto, o
pêndulo oscilará em um plano
vertical sob à ação da
gravidade.
O movimento é periódico e
chama-se período de
oscilação (T) ao tempo gasto
para uma oscilação completa
(ida e volta).

3. fio inextensível
e sem massa
massa
pendular

4. m
L
θ
Elementos
do pêndulo
simples:
θ  amplitude
L  comprimento
m  massa pendular

5. m
L
θ
Período de oscilação
para pequenas
amplitudes :
θ ≤ 10°
T = 2.π. L
g

6. Leis do pêndulo simples
1
O período de
oscilação não
depende da
amplitude (para
pequenas
amplitudes)
θ ≤ 10°
T = 2.π. L
g
Período de oscilação
para pequenas
amplitudes :
Note que θ não aparece na equação !

7. θ ≤ 10°
T = 2.π. L
g
Leis do pêndulo simples
2
O período de
oscilação não
depende da
massa pendular.
Note que m não aparece na equação !
Período de oscilação
para pequenas
amplitudes :

8. θ ≤ 10°
T = 2.π. L
g
Leis do pêndulo simples
3
O período de
oscilação é
diretamente
proporcional à
raiz quadrada do
comprimento.
Período de oscilação
para pequenas
amplitudes :

9. θ ≤ 10°
T = 2.π. L
g
Leis do pêndulo simples
4
O período de
oscilação é
inversamente
proporcional à
raiz quadrada
aceleração da
gravidade.
Período de oscilação
para pequenas
amplitudes :

10. θ ≤ 10°
T = 2.π. L
g
Leis do pêndulo simples
5
O plano de
oscilação de um
pêndulo simples
permanece
constante.
Período de oscilação
para pequenas
amplitudes :

11. Leis do pêndulo simples
5
O plano de
oscilação de um
pêndulo simples
permanece
constante.
O plano de oscilação do
pêndulo abaixo permanece
constante, mesmo que o
suporte sofra rotação.

12. Principais aplicações do
pêndulo simples :
Comprovação do movimento de
rotação da Terra
Determinação da aceleração da
gravidade

13. Comprovação do movimento de
rotação da Terra
Em 1600, Giordano Bruno
foi condenado à fogueira
pela Inquisição porque
acreditava que a Terra se
movia em torno do seu
eixo e em torno do Sol.
Trinta e três anos depois,
Galileu Galilei só não
teve o mesmo destino
porque renunciou à sua
convicção científica.
A dificuldade em
confirmar a rotação da
Terra reside no fato de
que se trata de uma
rotação muito lenta
(0,0007 rotações por
minuto).

14. Em 1851, o astrônomo
francês Foucault realizou
uma bela e simples
experiência capaz de
demonstrar a rotação da
Terra.
Com uma corda de 67
metros, fixa no teto do
Panteon de Paris, ele
suspendeu uma esfera de
ferro de 28 kg e imprimiu-
lhe um movimento
pendular.
Comprovação do movimento de
rotação da Terra

15. Na seqüência, o plano do
pêndulo passou a
apresentar uma lenta
rotação no sentido
horário. Este movimento
foi facilmente explicado a
partir da suposição de
que a Terra gira em torno
de seu eixo.
Comprovação do movimento de
rotação da Terra

16. No Equador não se percebe
movimento de rotação
No Pólo Norte o pêndulo dá
uma volta
completa a cada 24 horas
Em Paris o pêndulo
completa uma volta
a cada 31 horas e 47 min
Comportamento do
pêndulo de Foucault
Comprovação do movimento de
rotação da Terra

17. Jean Bernard
Leon Foucault
(1819-1868)
Em 1851, eu
demonstrei o
movimento de
rotação da
Terra.

18. Determinação da aceleração da
gravidade
Para se determinar a aceleração
da gravidade em um ponto
qualquer da Terra basta dispor de
um pêndulo simples, um
cronômetro e uma régua (ou
trena).

19. Determinação da aceleração da
gravidade
Com a régua (ou trena) mede-se o
comprimento do pêndulo  L
Com o cronômetro mede-se o período
de oscilação do pêndulo  T
T = 2.π. L
g
g = 4. π2
L
T2
isolando g

20. Determinação da aceleração da
gravidade
Exemplo
Determinaremos a aceleração da gravidade onde um pêndulo
de 1 metro oscila com um período de 2 segundos.
2 = 2.π. 1
g
T = 2.π. L
g
g = π2
g = 3,142
g = 9,86 m/s2

21. Pronto !
Você acabou de fazer uma
proveitosa revisão sobre esse
interessante sistema mecânico
denominado pêndulo simples, que
permite comprovar o movimento de
rotação terrestre e determinar a
aceleração da gravidade.