Congruência e Semelhança de Triângulos
•Transferir como PPTX, PDF•
3 gostaram•2,499 visualizações
Congruência e Semelhança de Triângulos
Denunciar
Compartilhar
Denunciar
Compartilhar
Recomendados
Mais conteúdo relacionado
Mais procurados
Mais procurados (20)
Folder de compostagem e vermicompostagem doméstica

Folder de compostagem e vermicompostagem doméstica
Destaque
ampliação e redução de figuras geometricas.Ampliação e redução de figuras geométricas, proporcionalidade uso do papel q...

Ampliação e redução de figuras geométricas, proporcionalidade uso do papel q...João Batista Barbosa Filho
Destaque (20)
Matemática - Exercícios Semelhança de Triângulos - Parte 2

Matemática - Exercícios Semelhança de Triângulos - Parte 2
Ampliação e redução de figuras geométricas, proporcionalidade uso do papel q...

Ampliação e redução de figuras geométricas, proporcionalidade uso do papel q...
Último
Aula de tema de redação desenvolvida pela professora Ana Augusta Lages, graduanda em Letras pela UFMGTema de redação - As dificuldades para barrar o casamento infantil no Brasil ...

Tema de redação - As dificuldades para barrar o casamento infantil no Brasil ...AnaAugustaLagesZuqui
Último (20)
Tema de redação - As dificuldades para barrar o casamento infantil no Brasil ...

Tema de redação - As dificuldades para barrar o casamento infantil no Brasil ...
Cópia de AULA 2- ENSINO FUNDAMENTAL ANOS INICIAIS - LÍNGUA PORTUGUESA.pptx

Cópia de AULA 2- ENSINO FUNDAMENTAL ANOS INICIAIS - LÍNGUA PORTUGUESA.pptx
Apresentação ISBET Jovem Aprendiz e Estágio 2023.pdf

Apresentação ISBET Jovem Aprendiz e Estágio 2023.pdf
Introdução às Funções 9º ano: Diagrama de flexas, Valor numérico de uma funçã...

Introdução às Funções 9º ano: Diagrama de flexas, Valor numérico de uma funçã...
O estudo do controle motor nada mais é do que o estudo da natureza do movimen...

O estudo do controle motor nada mais é do que o estudo da natureza do movimen...
Poesiamodernismo fase dois. 1930 prosa e poesiapptx

Poesiamodernismo fase dois. 1930 prosa e poesiapptx
O que é arte. Definição de arte. História da arte.

O que é arte. Definição de arte. História da arte.
Plano de aula Nova Escola períodos simples e composto parte 1.pptx

Plano de aula Nova Escola períodos simples e composto parte 1.pptx
Responde ou passa na HISTÓRIA - REVOLUÇÃO INDUSTRIAL - 8º ANO.pptx

Responde ou passa na HISTÓRIA - REVOLUÇÃO INDUSTRIAL - 8º ANO.pptx
Apresentação | Dia da Europa 2024 - Celebremos a União Europeia!

Apresentação | Dia da Europa 2024 - Celebremos a União Europeia!
Slides Lição 6, Betel, Ordenança para uma vida de obediência e submissão.pptx

Slides Lição 6, Betel, Ordenança para uma vida de obediência e submissão.pptx
A Revolução Francesa. Liberdade, Igualdade e Fraternidade são os direitos que...

A Revolução Francesa. Liberdade, Igualdade e Fraternidade são os direitos que...
8 Aula de predicado verbal e nominal - Predicativo do sujeito

8 Aula de predicado verbal e nominal - Predicativo do sujeito
Congruência e Semelhança de Triângulos
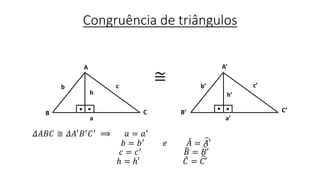
- 1. Congruência de triângulos ≅ 𝛥𝐴𝐵𝐶 ≅ 𝛥𝐴′ 𝐵′ 𝐶′ ⟹ 𝑎 = 𝑎′ 𝑏 = 𝑏′ 𝑒 𝐴 = 𝐴′ 𝑐 = 𝑐′ 𝐵 = 𝐵′ ℎ = ℎ′ 𝐶 = 𝐶′ A B C A’ B’ C’ h h’ a a’ b c b’ c’
- 2. 1º caso: LAL (lado-ângulo-lado) ≅ Critério: 𝑏 = 𝑏´ ⟹ 𝛥𝐴𝐵𝐶 ≅ 𝛥𝐴′ 𝐵′ 𝐶′ 𝑐 = 𝑐´ A = 𝐴′(α = β) c A C B’ b α A’ C’ B b’ c’ β
- 3. 2º caso: ALA (ângulo-lado-ângulo) Critério: 𝑎 = 𝑎′ 𝐶 = 𝐶′ ⟹ 𝛥𝐴𝐵𝐶 ≅ 𝛥𝐴′ 𝐵′ 𝐶′ 𝐵 = 𝐵′ B α A C a β A’ C’ B’ a’ βα
- 4. 3º caso: 𝐿𝐴𝐴 𝑜 (lado-ângulo-ângulo oposto) Critério: 𝑎 = 𝑎′ 𝐵 = 𝐵′ ⟹ 𝛥𝐴𝐵𝐶 ≅ 𝛥𝐴′ 𝐵′ 𝐶′ 𝐴 = 𝐴′ B A C a β A’ C’ B’ a’ β γ γ′
- 5. 4º caso: 𝐿𝐿𝐿 (lado-lado-lado) Critério: 𝑎 = 𝑎′ b = 𝑏′ ⟹ 𝛥𝐴𝐵𝐶 ≅ 𝛥𝐴′ 𝐵′ 𝐶′ c = 𝑐′ B C A b C’ A’ B’ c’ a c b’ a’
- 6. Semelhança de triângulos Dois triângulos são ditos semelhantes quando: 1º) É possível coloca-los na mesma posição, fazendo com que seus três lados sejam paralelos dois a dois. *Feito isto, teremos uma relação de proporção entre os lados destes triângulos. 2º) É necessário que os seus ângulos internos sejam congruentes (tenham mesma medida).
- 7. De acordo com a imagem que temos na apostila, temos 𝛥𝐷𝐸𝐶 sobreposto ao 𝛥𝐴𝐵𝐶. Assim, 𝛥𝐴𝐵𝐶 ≈ 𝛥𝐷𝐸𝐶 ⟺ 𝐴 = 𝐷 𝐵 = 𝐸 𝐶 = 𝐶 𝑒 𝐴𝐵 𝐷𝐸 = 𝐵𝐶 𝐸𝐶 = 𝐴𝐶 𝐷𝐶 = 𝑘 C A B D E
- 8. Ou também podemos separar os dois triângulos, conforme a representação na folha: 𝛥𝐴𝐵𝐶 ≈ 𝛥𝐷𝐸𝐹 ⟺ 𝐴 = 𝐷 𝐵 = 𝐸 𝐶 = 𝐹 𝑒 𝐴𝐵 𝐷𝐸 = 𝐵𝐶 𝐸𝐹 = 𝐶𝐴 𝐹𝐷 = 𝑘 𝑘 é a razão de semelhança. Observe que a razão entre os lados é determinada pela posição de acordo com os ângulos. A B C D E F
- 9. 1º caso: 𝐴𝐴 (ângulo-ângulo) Dois ângulos ordenadamente congruentes. 𝐵 = 𝐸 𝐶 = 𝐹 ⟹ 𝛥𝐴𝐵𝐶 ≈ 𝛥𝐷𝐸𝐹 A CB D E F
- 10. 2º caso: LAL (lado-ângulo-lado) *lados proporcionais* 𝐴𝐵 𝐷𝐸 = 𝐴𝐶 𝐷𝐹 𝐴 = 𝐷 ⟹ 𝛥𝐴𝐵𝐶 ≈ 𝛥𝐷𝐸𝐹 A B C D E F
- 11. 3º caso: LLL (lado-lado-lado) *lados proporcionais* 𝐴𝐵 𝐷𝐸 = 𝐴𝐶 𝐷𝐹 = 𝐵𝐶 𝐸𝐹 ⟹ 𝛥𝐴𝐵𝐶 ≈ 𝛥𝐷𝐸𝐹 A B C D E F
