O documento discute correlação, regressão linear e não linear em estatística. Estabelece como medir a força da relação entre variáveis e ajustar modelos de regressão para prever valores com base em dados observados. Inclui exemplos passo a passo de como calcular a correlação e determinar equações de regressão linear, quadrática e exponencial.

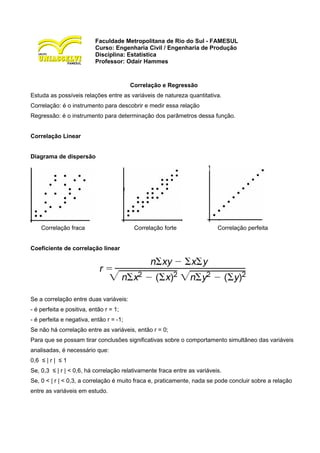
1. Faculdade Metropolitana de Rio do Sul - FAMESUL
Curso: Engenharia Civil / Engenharia de Produção
Disciplina: Estatística
Professor: Odair Hammes
Correlação e Regressão
Estuda as possíveis relações entre as variáveis de natureza quantitativa.
Correlação: é o instrumento para descobrir e medir essa relação
Regressão: é o instrumento para determinação dos parâmetros dessa função.
Correlação Linear
Diagrama de dispersão
Correlação fraca
Correlação forte
Correlação perfeita
Coeficiente de correlação linear
Se a correlação entre duas variáveis:
- é perfeita e positiva, então r = 1;
- é perfeita e negativa, então r = -1;
Se não há correlação entre as variáveis, então r = 0;
Para que se possam tirar conclusões significativas sobre o comportamento simultâneo das variáveis
analisadas, é necessário que:
0,6 ≤ | r | ≤ 1
Se, 0,3 ≤ | r | < 0,6, há correlação relativamente fraca entre as variáveis.
Se, 0 < | r | < 0,3, a correlação é muito fraca e, praticamente, nada se pode concluir sobre a relação
entre as variáveis em estudo.

2. Regressão Linear
Ajustamento da reta
Exemplos e exercícios
01. Uma população é composta por três pontos (x; y). São eles: (1; 2); (2; 2) e (3; 4).
a) Faça um diagrama de dispersão.
b) Complete a tabela:
x
1
2
d) Determine a reta ajustada a essa correlação.
2
3
c) Calcule o coeficiente de correlação linear.
y
2
4
xy
x2
y2

3. 02. Uma população é composta por quatro pontos (x; y). São eles: (1; 1) (2; 2) (3; 2) e (4; 3).
a) Faça um diagrama de dispersão.
b) Complete a tabela:
x
1
2
2
4
d) Determine a reta ajustada a essa correlação.
2
3
c) Calcule o coeficiente de correlação linear.
y
1
3
xy
x2
y2

4. 03. Considere uma amostra aleatória, formada por dez dos 98 alunos de uma classe da faculdade A
e pelas notas obtidas por eles em Matemática e Estatística:
x
Notas
N°
y
xy
x2
y2
Matemática
Estatística
5
6
30
25
36
x
y
8
9
72
64
81
8
5
6
7
8
56
49
64
24
8
9
10
10
100
100
100
38
7
8
6
5
30
36
25
44
10
10
7
7
49
49
49
58
6
5
9
8
72
81
64
59
7
7
3
4
12
9
16
72
9
8
8
6
48
64
36
80
3
4
2
2
4
4
4
92
8
6
∑=65
∑=65
∑=473
∑=481
∑=475
95
2
2
a) Faça um diagrama de dispersão.
c) Calcule o coeficiente de correlação linear.
d) Determine a reta ajustada a essa correlação.

5. 04. A tabela a seguir apresenta valores que mostram como o comprimento de uma barra de aço varia
conforme a temperatura:
Temperatura (°C)
10
15
20
25
30
Comprimento (mm)
1 003
1 005
1 010
1 011
1 014
Determine:
a) o coeficiente de correlação;
b) a reta ajustada a essa correlação;
c) o valor estimado do comprimento da barra para a temperatura de 18°C;
d) o valor estimado do comprimento da barra para a temperatura de 35°C;
05. Uma bola de tênis é solta de várias alturas, e a altura da bola na primeira rebatida é medida. Use
os dados da tabela para achar a reta de mínimos quadrados para a altura das rebatidas y em função
da altura inicial x.
x (cm)
20
40
48
60
80
100
y (cm)
14,5
31
36
45,5
59
73,5
06. A Lei de Hooke diz que o comprimento de uma mola é uma função linear de força F aplicada
sobre uma mola. Assim, existem constantes a e b tais que:
L= a + bF
A tabela mostra o resultado de pendurarmos vários pesos na corda.
F(onça)
2
4
6
8
L(pol.)
7,4
9,6
11,5
13,6
a) Determine as constantes a e b achando a reta de mínimos quadrados para esses dados.
b) Estime o comprimento da mola, considerando m peso de 5 onças pendurado nela.
07. Os comprimentos medidos de uma barra metálica (y) em oito temperaturas diferentes (x)
resultaram na tabela abaixo:
x (ºC)
25,00
50,00
75,00
100,0
125,0
150,0
175,0
200,0
y (mm)
100,07
100,12
100,16
100,21
100,26
100,30
100,35
100,40
Determine:
a) o coeficiente de correlação;
b) a reta ajustada a essa correlação;
Regressão não linear

6. Regressão quadrática
y = a + bx + cx2
01. Encontre a parábola que tem a melhor aproximação por mínimos quadrados para os pontos:
(-1; 1) (0; -1) (1; 0) e (2; 2).
02. Quando um objeto é arremessado para cima, a Segunda Lei de Newton afirma que sua altura s(t)
no tempo t é dada por:
s(t) = s0 + v0t + ½gt2
onde v0 é a velocidade inicial e g é a constante de aceleração da gravidade. Considere as medidas
mostradas na tabela.
Tempo (s)
Altura (m)
0,5
11
1
17
1,5
21
2
23
3
18
a) Encontre a aproximação quadrática por mínimos quadrados para esses dados.
b) Estime a altura na qual o objeto foi solto (em m), sua velocidade inicial (em m/s) e sua aceleração
da gravidade (em m/s2).
Regressão exponencial
y = a.ebx
01. Uma amostra de 200 mg de polônio-210 radioativa é observada conforme ela decresce. A tabela
mostra a massa restante em vários tempos.
Tempo (dias)
Massa (mg)
0
200
30
172
60
148
90
128
Assumindo um modelo exponencial decrescente, utilize mínimos quadrados para encontrar a meiavida do polônio-210.
02. A tabela apresenta a população do mundo em intervalos de dez anos, referentes à segunda
metade do século XX. Supondo um modelo de crescimento exponencial, encontre a taxa de
crescimento relativo e preveja a população do mundo em 2010.
Ano
População
(em bilhões)
1950
1960
1970
1980
1990
2000
2,56
3,04
3,71
4,46
5,28
6,08

7. Regressão quadrática
y = a + bx + cx2
01. Encontre a parábola que tem a melhor aproximação por mínimos quadrados para os pontos:
(-1; 1) (0; -1) (1; 0) e (2; 2).
02. Quando um objeto é arremessado para cima, a Segunda Lei de Newton afirma que sua altura s(t)
no tempo t é dada por:
s(t) = s0 + v0t + ½gt2
onde v0 é a velocidade inicial e g é a constante de aceleração da gravidade. Considere as medidas
mostradas na tabela.
Tempo (s)
Altura (m)
0,5
11
1
17
1,5
21
2
23
3
18
a) Encontre a aproximação quadrática por mínimos quadrados para esses dados.
b) Estime a altura na qual o objeto foi solto (em m), sua velocidade inicial (em m/s) e sua aceleração
da gravidade (em m/s2).
Regressão exponencial
y = a.ebx
01. Uma amostra de 200 mg de polônio-210 radioativa é observada conforme ela decresce. A tabela
mostra a massa restante em vários tempos.
Tempo (dias)
Massa (mg)
0
200
30
172
60
148
90
128
Assumindo um modelo exponencial decrescente, utilize mínimos quadrados para encontrar a meiavida do polônio-210.
02. A tabela apresenta a população do mundo em intervalos de dez anos, referentes à segunda
metade do século XX. Supondo um modelo de crescimento exponencial, encontre a taxa de
crescimento relativo e preveja a população do mundo em 2010.
Ano
População
(em bilhões)
1950
1960
1970
1980
1990
2000
2,56
3,04
3,71
4,46
5,28
6,08