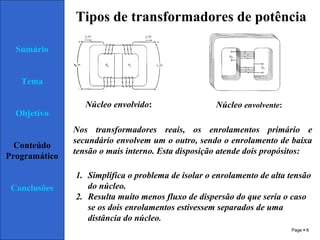
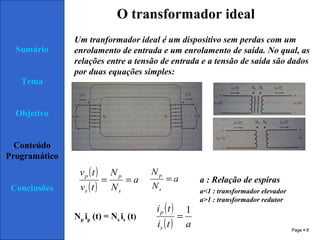
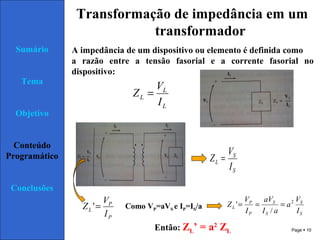
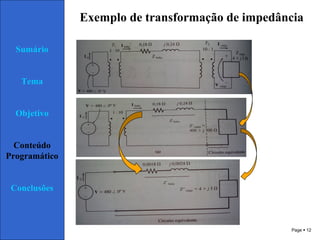
1) O documento discute transformadores, incluindo sua teoria de operação, tipos, e circuito equivalente.
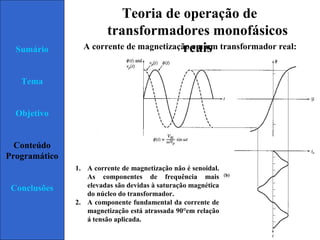
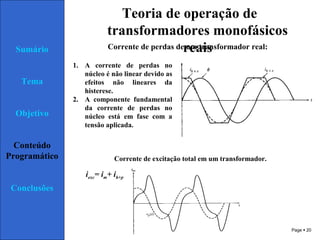
2) É explicado que um transformador real tem componentes de corrente de magnetização e perdas que afetam sua operação em comparação com um transformador ideal.
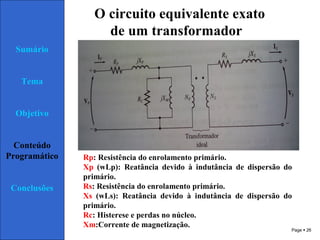
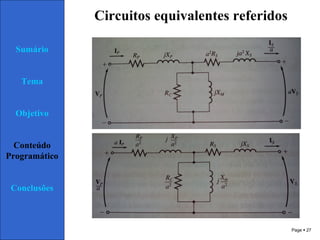
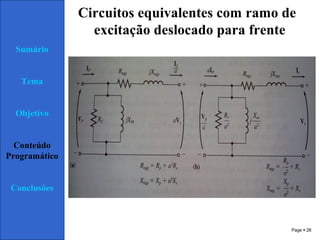
3) O circuito equivalente de um transformador contém elementos que representam suas perdas no núcleo, cobre e fluxo de dispersão.