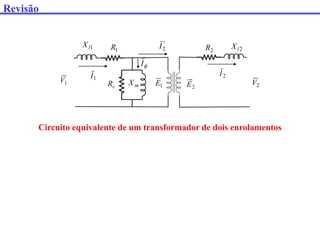
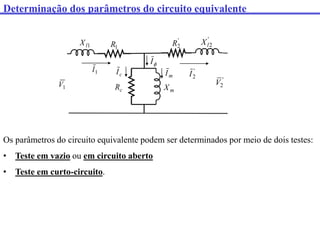
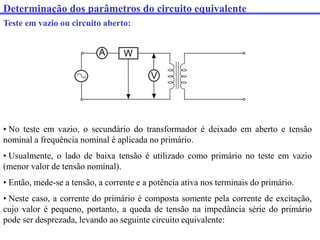
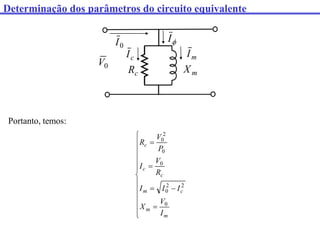
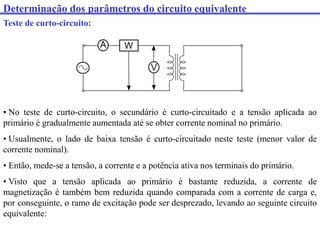
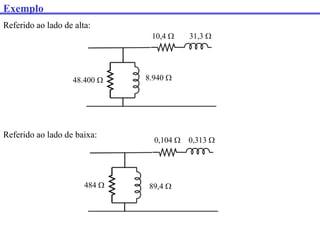
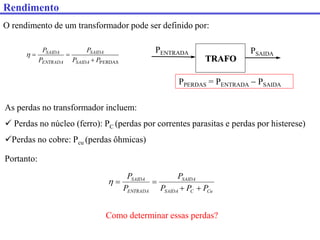
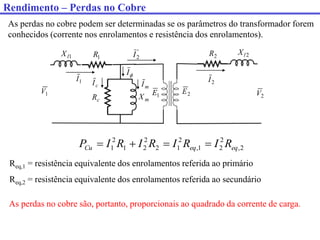
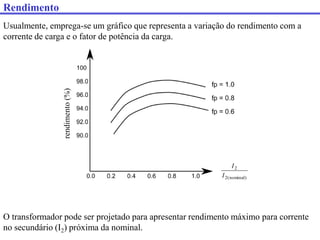
Este documento discute transformadores, incluindo: (1) como determinar os parâmetros do circuito equivalente de um transformador por meio de testes em vazio e curto-circuito, (2) como calcular a regulação de tensão e (3) fatores que afetam o rendimento de um transformador.

1. SEL 329 – CONVERSÃO
ELETROMECÂNICA DE ENERGIA
Aula 08

2. Revisão
1
V 1
I 2
I
1
R
1
l
X 2
l
X
2
R
c
R m
X 2
V
1
E 2
E

I
'
2
I
Circuito equivalente de um transformador de dois enrolamentos

3. Tópicos da Aula de Hoje
• Transformadores
 Obtenção dos parâmetros do circuito equivalente
 Regulação
 Rendimento

4. Determinação dos parâmetros do circuito equivalente
1
V
1
R
1
l
X
1
I '
2
I
'
2
V
'
2
l
X
'
2
R
c
R m
X 2
V

I
c
I m
I
Os parâmetros do circuito equivalente podem ser determinados por meio de dois testes:
• Teste em vazio ou em circuito aberto
• Teste em curto-circuito.

5. Determinação dos parâmetros do circuito equivalente
Teste em vazio ou circuito aberto:
• No teste em vazio, o secundário do transformador é deixado em aberto e tensão
nominal a frequência nominal é aplicada no primário.
• Usualmente, o lado de baixa tensão é utilizado como primário no teste em vazio
(menor valor de tensão nominal).
• Então, mede-se a tensão, a corrente e a potência ativa nos terminais do primário.
• Neste caso, a corrente do primário é composta somente pela corrente de excitação,
cujo valor é pequeno, portanto, a queda de tensão na impedância série do primário
pode ser desprezada, levando ao seguinte circuito equivalente:

6. Determinação dos parâmetros do circuito equivalente
Portanto, temos:


















m
m
c
m
c
c
c
I
V
X
I
I
I
R
V
I
P
V
R
0
2
2
0
0
0
2
0
0
V

I
0
I
c
R m
X
c
I m
I

7. Determinação dos parâmetros do circuito equivalente
Teste de curto-circuito:
• No teste de curto-circuito, o secundário é curto-circuitado e a tensão aplicada ao
primário é gradualmente aumentada até se obter corrente nominal no primário.
• Usualmente, o lado de baixa tensão é curto-circuitado neste teste (menor valor de
corrente nominal).
• Então, mede-se a tensão, a corrente e a potência ativa nos terminais do primário.
• Visto que a tensão aplicada ao primário é bastante reduzida, a corrente de
magnetização é também bem reduzida quando comparada com a corrente de carga e,
por conseguinte, o ramo de excitação pode ser desprezado, levando ao seguinte circuito
equivalente:

8. Determinação dos parâmetros do circuito equivalente
cc
V
'
2
1 l
X
X 
'
2
1 R
R 
'
2
2
I
a
I
Icc 

Portanto, temos:















2
2
2
eq
eq
eq
cc
cc
eq
cc
cc
eq
R
Z
X
I
V
Z
I
P
R
Caso seja necessário determinar R1, R2, X1 e X2, o seguinte procedimento é utilizado.
Considera-se que em um transformador bem projetado as perdas ôhmicas e a dispersão
sejam iguais nos enrolamentos do primário e do secundário. Assim, temos:









'
2
1
'
2
1
X
X
R
R
R
R
eq
eq

9. Determinação dos parâmetros do circuito equivalente

















2
2
1
2
2
1
2
2
2
2
a
R
R
R
R
a
X
X
X
X
eq
eq
eq
eq

10. Exemplo
A partir de testes realizados em um transformador monofásico de 10 kVA, 2200/220 V,
60 Hz, os seguintes resultados são obtidos:
teste em vazio teste de curto-circuito
Voltímetro: 220 V 150 V
Amperímetro: 2,5 A 4,55 A
Wattímetro: 100 W 215 W
(a) calcule os parâmetros dos circuito equivalente referidos ao lado de baixa e alta
tensão.
(b) expresse a corrente de excitação em termos da corrente nominal.

11. Exemplo
(a) O teste em vazio foi realizado aplicando-se tensão nominal ao lado de baixa tensão.
Assim, temos:
- Perdas no núcleo:





 484
100
2202
0
2
0
2
0
0
P
V
R
R
V
P c
c
- Corrente de perdas:
A
45
,
0
484
220
0



c
c
R
V
I
- Corrente de magnetização:
A
46
,
2
45
,
0
5
,
2
A
5
,
2
2
2
2
2
0







c
m I
I
I
I
I


- Reatância de magnetização:



 4
,
89
46
,
2
220
0
m
m
I
V
X

12. Exemplo
Referido ao lado de baixa:
Rc = 484  e Xm = 89,4 
Referido ao lado de alta (a = VH/VL = 2200/220 = 10):
Rc = 48.400  e Xm = 8.940 
O teste de curto-circuito foi realizado aplicando-se tensão no lado de alta tensão até
obter corrente nominal (10 kVA/2,2 kV = 4,55 A). Assim, temos:
















3
,
31
4
,
10
97
,
32
97
,
32
55
,
4
150
4
,
10
55
,
4
215
2
2
2
2
2
2
2
eq
eq
eq
cc
cc
eq
cc
cc
eq
cc
eq
cc
R
Z
X
I
V
Z
I
P
R
I
R
P
Referido ao lado de alta:
Req = 10,4  e Xeq = 31,3 
Referido ao lado de baixa (a = VL/VH = 220/2200 = 0,1):
Req = 0,104  e Xeq = 0,313 

13. Exemplo
10,4  31,3 
48.400  8.940 
Referido ao lado de baixa:
0,104  0,313 
484  89,4 
Referido ao lado de alta:

14. Exemplo
(b) expresse a corrente de excitação em termos da corrente nominal
No teste em vazio, a corrente medida é igual à corrente de excitação. Além disso, o
teste é realizado do lado de baixa, assim, temos:
%
5
,
5
100
5
,
45
5
,
2
100
)
V
220
/
VA
000
.
10
(
5
,
2





n
I
I

15. Regulação de Tensão
Um dos critérios de desempenho de um transformador projetado para suprir potência
com tensão aproximadamente constante para uma carga é o de regulação de tensão. Tal
critério indica o grau de constância da tensão de saída quando a carga é variada.
A regulação de tensão do transformador é definida como sendo a variação da tensão
do secundário em condições de carga e em vazio, tomada como porcentagem da
tensão a plena carga, com tensão do primário mantida constante, ou seja:
100
%
em
Regulação
carga
,
2
carga
,
2
vazio
,
2



V
V
V
A tensão do secundário quando o transformador está em vazio é:
a
V
V 1
vazio
,
2 
Quando uma carga é conectada ao secundário, a tensão terminal é dada por:
2
vazio
,
2
carga
,
2 V
V
V 



16. Regulação de Tensão
• A tensão no secundário pode aumentar ou diminuir, dependendo da característica da
carga.
• A variação da tensão ocorre devido à queda de tensão (V = IZeq) associada à
impedância interna do transformador.
• Para muitos tipos de carga, grandes variações de tensão são indesejáveis. Portanto, os
transformadores são projetados de forma a apresentarem pequenos valores de Zeq.
• O termo regulação de tensão é usado para caracterizar a variação de tensão do
transformador com o carregamento.

17. Regulação de Tensão
A regulação de tensão pode também ser calculada para o circuito refletido ao primário,
ou seja:
100
'
'
'
%
em
Regulação
carga
,
2
carga
,
2
vazio
,
2



V
V
V
V1
V2
V’2
Zeq = Req + j Xeq
Além disso, para efeitos de análise e projeto, considera-se que a tensão sob carga
V’2,carga é igual à tensão nominal de placa do transformador (carga).
V’2,carga= V’2,nominal
Portanto, temos:
eq
eq
eq Z
I
V
X
I
j
R
I
V
V '
2
'
2
'
2
'
2
'
2
1 





18. Regulação de Tensão
Em vazio, I’2 = 0  V’2,vazio = V1
100
'
'
%
em
Regulação
carga
,
2
carga
,
2
1



V
V
V
Diagrama fasorial:
Seja uma carga dada por Zcarga 2, um transformador cuja impedância equivalente é
dada por Zeq = Req + jXeq = Zeq eq e considerando V’2 como referência, temos
Obs: V1 deve ser ajustada em função da carga para que V2 sob carga opere no valor
nominal (ou que V2 seja constante).
'
2
I
'
2
V
1
V
'
2
I
Req
'
2
I
Xeq
'
2
I
Zeq
2

eq

 
2

19. Regulação de Tensão
A magnitude de V1 será máxima quando V estiver em fase com V’2, ou seja:
2 + eq= 0  2 =  eq
Portanto, a regulação máxima ocorre quando o ângulo do fator de potência da
carga é o mesmo da impedância equivalente do transformador e com corrente
atrasada em relação à tensão.
Regulação de tensão alta significa maiores variações de tensão quando o carregamento
do transformador aumenta.
Conhecendo-se a carga a ser atendida (Zcarga 2), o transformador pode ser projetado
(Zeq eq) de forma a respeitar um critério de regulação máxima de, por exemplo, 5%.

20. Regulação de Tensão
Observações:
-A regulação de tensão de um transformador depende de sua impedância interna e das
características da carga.
- Regulação de tensão positiva significa que se tensão nominal for aplicada ao primário
a tensão efetiva na carga será menor que a nominal (carga indutiva).
- Regulação de tensão negativa significa que se tensão nominal for aplicada ao
primário a tensão efetiva na carga será maior que a nominal (carga capacitiva).
- A tensão primária deve ser ajustada de acordo com a carga para que se tenha tensão
nominal no secundário.

21. • Os transformadores são projetados para operarem com alto rendimento.
• Os seguintes aspectos contribuem para que os transformadores apresentem valores
baixos de perdas:
 O transformador é uma máquina estática, ou seja, não tem partes rotativas, não
apresentando, portanto, perdas por atrito no eixo e por resistência do ar no
entreferro.
O núcleo é constituído por placas laminadas e dopadas de materiais de alta
resistência elétrica, as quais têm o objetivo de minimizar as perdas por correntes
parasitas.
Materiais com alta permeabilidade magnética são utilizados para diminuir as
perdas por histerese.
Transformadores de alta potência apresentam rendimento maior que 99 %.
Rendimento

22. O rendimento de um transformador pode ser definido por:
PERDAS
P
P
P
P
P
SAIDA
SAIDA
ENTRADA
SAIDA




As perdas no transformador incluem:
 Perdas no núcleo (ferro): PC (perdas por correntes parasitas e perdas por histerese)
Perdas no cobre: Pcu (perdas ôhmicas)
PENTRADA
TRAFO
PPERDAS = PENTRADA  PSAIDA
PSAIDA
Portanto:
Cu
C
SAIDA
SAIDA
ENTRADA
SAIDA
P
P
P
P
P
P





Como determinar essas perdas?
Rendimento

23. As perdas no cobre podem ser determinadas se os parâmetros do transformador forem
conhecidos (corrente nos enrolamentos e resistência dos enrolamentos).
1
V
1
I 2
I
1
R
1
l
X 2
l
X
2
R
c
R m
X 2
V
1
E 2
E

I
'
2
I
c
I m
I
2
,
2
2
1
,
2
1
2
2
2
1
2
1 eq
eq
Cu R
I
R
I
R
I
R
I
P 



Req,1 = resistência equivalente dos enrolamentos referida ao primário
Req,2 = resistência equivalente dos enrolamentos referida ao secundário
As perdas no cobre são, portanto, proporcionais ao quadrado da corrente de carga.
Rendimento – Perdas no Cobre

24. As perdas no núcleo podem ser determinadas pelo teste em vazio, ou a partir dos
parâmetros do circuito equivalente.
C
C
C
C
C
C
R
E
R
E
R
I
R
P
2
1
2
1
2











1
E

I
m
I
c
I
Rc Xm
As perdas no núcleo são, portanto, proporcionais ao quadrado da tensão aplicada.
Rendimento – Perdas no Ferro (Núcleo)

25. Finalmente, a partir da obtenção dos valores de perdas no núcleo e no cobre, o
rendimento do transformador em estudo pode ser obtido, para qualquer condição de
operação por:
2
,
2
2
2
1
2
2
2
2
2
2
cos
cos
eq
C
ENTRADA
SAIDA
R
I
R
E
I
V
I
V
P
P







A potência de saída do transformador pode ser obtida por:
2
2
2 cos
I
V
PSAIDA 
onde, V2 e I2 representam a tensão e corrente na saída (carga) do transformador,
respectivamente. E o ângulo θ2 representa a defasagem angular entre os fasores V2 e I2,
ou seja θ2 é o ângulo da carga.
 Considerando que a tensão na carga é mantida constante e que as perdas no núcleo
praticamente não variam com o carregamento, pode-se concluir que o rendimento
depende da corrente exigida pela carga (I2) e do fator de potência da carga (cosθ2)
2
,
2
2
2
2
2
2
2
2
cos
cos
eq
C
ENTRADA
SAIDA
R
I
P
I
V
I
V
P
P







Rendimento – Potência de Saída

26. Considerando a tensão na carga (V2) e o fator de potência (cosθ2) constantes, e
avaliando somente a variação da corrente de carga (I2), tem-se que o rendimento
máximo ocorre para:
0
2

dI
d
   
 
0
cos
2
cos
cos
cos
cos
2
2
,
2
2
2
2
2
2
,
2
2
2
2
2
2
2
,
2
2
2
2
2
2
2
2








eq
C
eq
eq
C
R
I
P
I
V
R
I
V
I
V
R
I
P
I
V
V
dI
d






Lembrando que:
2
'
'
'
g
f
g
g
f
g
f 









Temos que:
Condições para Rendimento Máximo

27. Logo, temos que:
2
,
2
2
2
2
2
2
,
2
2
2
2
2 2
cos
cos eq
eq
C R
I
I
V
R
I
P
I
V 


 

E, finalmente, isolando PC:
Cu
eq
C P
R
I
P 
 2
,
2
2
Do resultado acima, pode-se concluir que o rendimento máximo ocorre quando as
perdas no núcleo se igualam às perdas no cobre.
Condições para Rendimento Máximo

28. Considerando agora somente a variação do ângulo θ2, tem-se que o rendimento máximo
ocorre para:
0
2



d
d
   
 
0
cos
cos
cos
2
2
,
2
2
2
2
2
2
2
2
2
2
2
2
,
2
2
2
2
2
2
2
2
2









eq
C
eq
C
R
I
P
I
V
sen
I
V
I
V
R
I
P
I
V
sen
I
V
d
d







Temos que:
Simplificando a expressão acima, obtém-se:
  0
2
2
,
2
2
2
2 
 
sen
R
I
P
I
V eq
C
Para que a equação acima seja válida:
unitário)
potência
de
(fator
1
θ
cos
0
θ
0
2
2
2




ou
sen
Portanto, o rendimento máximo ocorre para quando o fator de potência da carga
(cosθ2) é unitário.
Condições para Rendimento Máximo

29. Usualmente, emprega-se um gráfico que representa a variação do rendimento com a
corrente de carga e o fator de potência da carga.
rendimento
(%)
)
nominal
(
2
2
I
I
O transformador pode ser projetado para apresentar rendimento máximo para corrente
no secundário (I2) próxima da nominal.
Rendimento

30. Transformadores utilizados para atender as cargas do secundário em sistemas de
distribuição usualmente atendem uma carga bastante variável. Neste caso, uma figura
de mérito importante é o rendimento diário (ou rendimento energético). O qual pode ser
calculado por:
horas
24
em
perdas
horas
24
em
saída
de
energia
horas
24
em
saída
de
energia
horas
24
em
entrada
de
energia
horas
24
em
saída
de
energia



D

Rendimento Diário

31. Para o transformador analisado anteriormente, determine:
(a) o rendimento para carregamento de 75% da carga nominal e fp = 0,6.
(b) A potência de saída para que o rendimento seja máximo e o valor do rendimento máximo.
Para qual valor de porcentagem da carga nominal, o rendimento máximo ocorre?
(c) Qual o rendimento com carga nominal?
teste em vazio teste de curto-circuito
Voltímetro: 220 V 150 V
Amperímetro: 2,5 A 4,55 A
Wattímetro: 100 W 215 W
Referido ao lado de alta:
10,4  31,3 
48.400  8.940 
Referido ao lado de baixa:
0,104  0,313 
484  89,4 
Exemplo

32. (a)
W
4500
6
,
0
10000
75
,
0
cos
75
,
0
carga)
da
potência
de
(fator
6
,
0
cos
ador)
transform
do
nominal
(potência
VA
10000
SAIDA
N









N
S
P
S
Cu
C
SAIDA
SAIDA
ENTRADA
SAIDA
P
P
P
P
P
P





vazio)
a
teste
do
núcleo
no
(perdas
W
100
C 
P
(1)
(2)
(3)
  alta)
de
lado
do
parâmetros
com
(calculado
W
121
4
,
10
55
,
4
75
,
0 2
2




 eq
H
Cu R
I
P
%
32
,
95
%
100
121
100
4500
4500






ENTRADA
SAIDA
P
P

Portanto:
Exemplo

33. (b) Sabemos que para rendimento máximo:
W
6820
1
31
220
cos 2
2
2
max




 

I
V
PSAIDA
A partir da condição acima, a corrente de carga I2 pode ser determinada:
Logo, a potência de saída pode ser obtida por:
E o valor do rendimento máximo é :
%
15
,
97
%
100
100
100
6820
6820








Cu
C
ENTRADA
SAIDA
P
P
P
P

1,0
fp
e
W
100 

 CU
C P
P
A
31
104
,
0
100
100 2
2
2 



 I
R
I
P eq
Cu
Obs 2: Resistência Req do lado de baixa
Saída em kVA = 6,82
kVA nominal = 10
Portanto, o rendimento máximo max ocorre para 68,2% do carregamento nominal
Obs 1: INominal,Baixa = 45,5 A
Exemplo

34. (c) Rendimento  para carga nominal:
W
10000
5
,
45
220
cos 2
2
2 

 x
I
V
PSAIDA 
para fp = 1,0 => melhor caso
para fp = 0,8
%
94
,
96
%
100
7
,
215
100
10000
10000








Cu
C
ENTRADA
SAIDA
P
P
P
P

W
7
,
215
4
,
10
A,
55
,
4 ,
2
, 




 H
eq
H
Cu
H
eq
H R
I
P
R
I
Obs: Transformadores devem ser dimensionados para atender carga próxima da nominal
W
8008
8
,
0
5
,
45
220
cos 2
2
2 



 
I
V
PSAIDA
%
21
,
96
%
100
7
,
215
100
8008
8008








Cu
C
ENTRADA
SAIDA
P
P
P
P

Exemplo

35. Próxima Aula
• Polaridade de transformadores
• Autotransformadores
• Transformadores Trifásicos