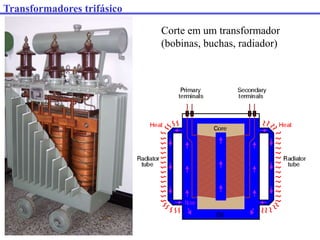
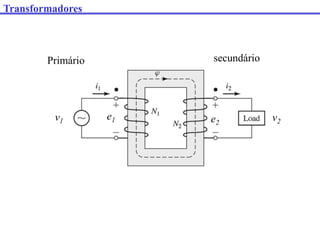
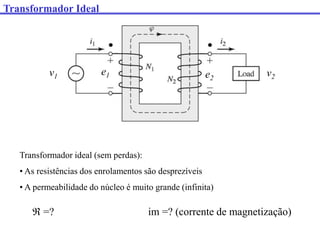
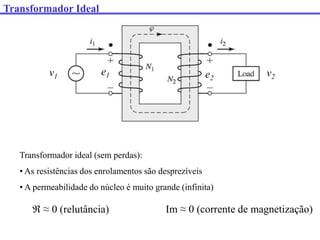
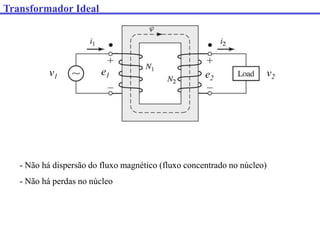
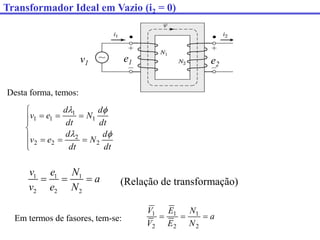
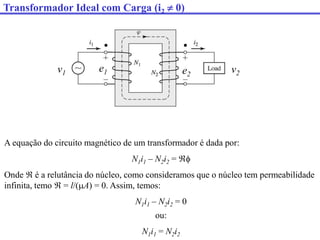
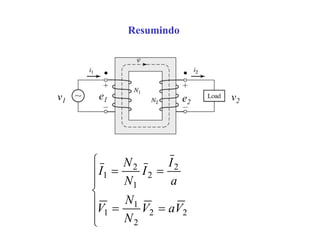
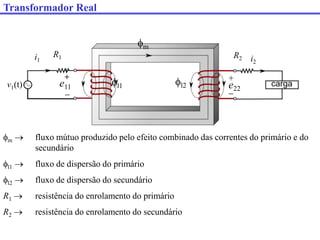
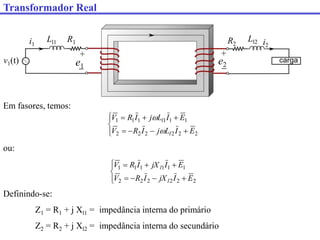
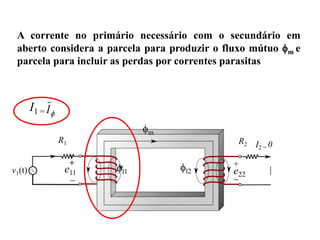
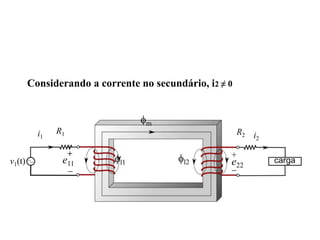
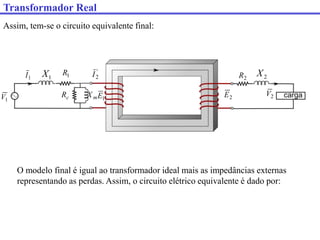
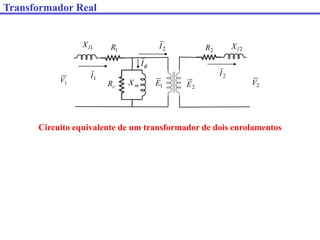
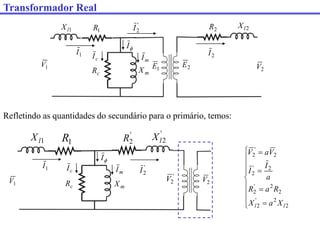
O documento descreve os principais componentes e características de transformadores. Transformadores são utilizados para transferir energia elétrica entre circuitos com diferentes níveis de tensão por meio de um campo magnético. São descritos transformadores monofásicos, trifásicos e seus principais usos em sistemas de distribuição e industriais.