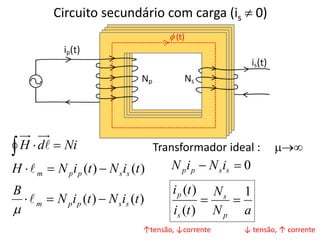
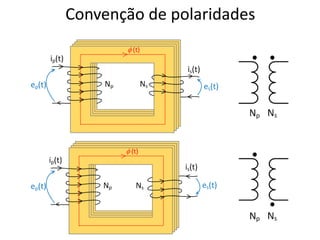
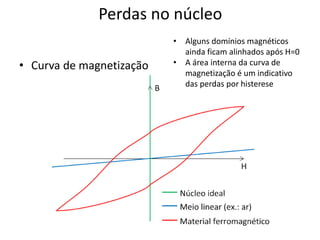
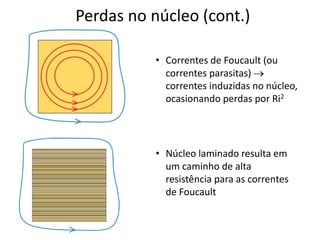
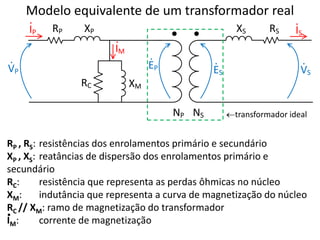
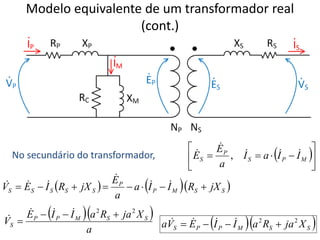
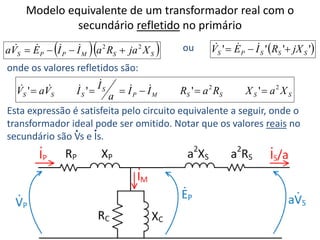
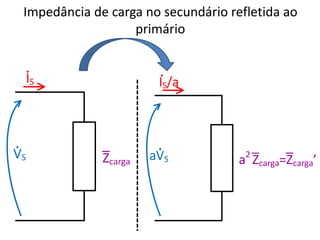
O documento resume conceitos fundamentais de eletromagnetismo e transformadores, incluindo: (1) a Lei de Ampère, fluxo magnético e indução magnética; (2) o funcionamento de transformadores ideais e reais, considerando perdas no núcleo e nos enrolamentos; (3) as relações entre grandezas elétricas nos circuites primário e secundário.

1. PEA2290
Transformadores

2. Lei de Ampére:
conc
C
i
dl
H 


conc
i
H = vetor campo magnético ou intensidade magnética [A/m]
= corrente concatenada com o contorno C
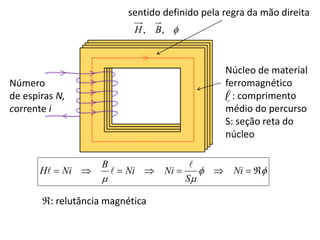
Revisão de conceitos de eletromagnetismo
Ni
dl
H
C



Bobina com N
espiras, corrente i

3. Vetor indução magnética ou densidade de fluxo :
B
H
B 

= indução magnética [T]
 = permeabilidade magnética [H/m]
0 (vácuo) = 410-7 H/m
Fluxo magnético  :
 

S
dS
B

 = fluxo magnético [Wb=Tm2], valor escalar
= vetor normal à superfície S, com módulo igual a dS
B
dS

4. 










 Ni
S
Ni
Ni
B
Ni
H




,
, B
H
Núcleo de material
ferromagnético
: comprimento
médio do percurso
S: seção reta do
núcleo

sentido definido pela regra da mão direita
Número
de espiras N,
corrente i
: relutância magnética

5. 


Ni
Ni também é chamada de “força
magnetomotriz” (fmm)

Ni E
i
R
Circuito elétrico análogo
i
R
E
i
S
i
S
E




 

Circuito magnético Circuito elétrico análogo
Relutância: Resistência:
Fluxo magnético  Corrente elétrica i
fmm = Ni fem = E
S


1


S
S
R




1


E também é chamada de “força
eletromotriz” da fonte (fem)

6. Transformadores
• Dispositivo que converte um nível de tensão
em outro nível de tensão pela ação da
variação do fluxo magnético
• A possibilidade de elevação e redução
eficiente do nível de tensão viabilizou a
transmissão de energia por distâncias
consideráveis em corrente alternada
– Maior tensão -> menor corrente -> menos perdas

7. Lei de Faraday:
Fluxo magnético variável induz uma tensão:
dt
d
N
dt
d
eind




   
dt
di
L
dt
Li
d
dt
N
Li
d
N
e
i
N
L ind 





Indutância:
Corrente senoidal -> fluxo magnético senoidal ->
variável no tempo

8. Transformador ideal
• Permeabilidade magnética  
–  (relutância) = 0
– Não há dispersão no fluxo magnético: todo o fluxo
é confinado ao núcleo
• Corrente de magnetização = 0
• Perdas no núcleo = 0
• Perdas Joule nos enrolamentos = 0

9. ep(t)
 (t)
es(t)
ip(t)
Enrolamento
primário,
Np espiras
Enrolamento
secundário,
Ns espiras
p
p
p
p
p
p
N
t
e
dt
d
dt
d
N
t
e
)
(
)
(




s
s
s
s
s
s
N
t
e
dt
d
dt
d
N
t
e
)
(
)
(




s
p 
 
a
N
N
t
e
t
e
s
p
s
p


)
(
)
(

10. Circuito secundário com carga (is  0)
)
(
)
(
)
(
)
(
t
i
N
t
i
N
B
t
i
N
t
i
N
H
Ni
d
H
s
s
p
p
m
s
s
p
p
m













Transformador ideal : 
0

 s
s
p
p i
N
i
N
a
N
N
t
i
t
i
p
s
s
p 1
)
(
)
(


↑tensão, ↓corrente ↓ tensão, ↑ corrente

11. Relações de tensão, corrente e potência em um transformador ideal
a
N
N
t
e
t
e
s
p
s
p


)
(
)
(
a
N
N
t
i
t
i
p
s
s
p 1
)
(
)
(


)
(
)
(
)
(
)
(
)
(
)
( t
i
t
e
N
N
t
i
N
N
t
e
t
i
t
e p
p
s
p
p
p
s
p
s
s 



potências
correntes
tensões
a
N
N
E
E
s
p
S
P




a
N
N
I
I
s
p
S
P 1




S
S
S
P
P
P S
I
E
I
E
S 

 *
* 




12. Convenção de polaridades

13. Transformador real
• Permeabilidade magnética finita
–  (relutância)  0
– Existe certa dispersão no fluxo magnético pelo ar,
percorrendo um caminho de alta relutância (baixa
permeabilidade)
• Corrente de magnetização  0
• Perdas no núcleo  0
• Perdas Joule nos enrolamentos  0

14. Transformador real: corrente de
magnetização
• Circuito secundário em aberto (sem carga)
– Corrente no primário: corrente de magnetização
= corrente necessária para produzir o fluxo no
núcleo magnético, através da orientação dos
domínios do material.

15. Perdas no núcleo
• Curva de magnetização
• Alguns domínios magnéticos
ainda ficam alinhados após H=0
• A área interna da curva de
magnetização é um indicativo
das perdas por histerese

16. Perdas no núcleo (cont.)
• Correntes de Foucault (ou
correntes parasitas) 
correntes induzidas no núcleo,
ocasionando perdas por Ri2
• Núcleo laminado resulta em
um caminho de alta
resistência para as correntes
de Foucault

17. Modelo equivalente de um transformador real
RP , RS: resistências dos enrolamentos primário e secundário
XP , XS: reatâncias de dispersão dos enrolamentos primário e
secundário
RC: resistência que representa as perdas ôhmicas no núcleo
XM: indutância que representa a curva de magnetização do núcleo
RC // XM: ramo de magnetização do transformador
IM: corrente de magnetização
•
RP XP XS RS
RC XM
NP NS
VP
.
IP
.
IM
.
EP
.
ES
.
VS
.
IS
.
transformador ideal

18.     
S
S
M
P
P
S
S
S
S
S jX
R
I
I
a
a
E
jX
R
I
E
V 






 





 








 M
P
S
P
S I
I
a
I
a
E
E 



 ,
  
S
S
M
P
P
S X
ja
R
a
I
I
E
V
a 2
2



 



No secundário do transformador,
Modelo equivalente de um transformador real
(cont.)
  
a
X
ja
R
a
I
I
E
V S
S
M
P
P
S
2
2









19. Modelo equivalente de um transformador real com o
secundário refletido no primário
  
S
S
M
P
P
S X
ja
R
a
I
I
E
V
a 2
2



 


  
'
'
'
' S
S
S
P
S jX
R
I
E
V 

 


S
S
S
S
M
P
S
S
S
S X
a
X
R
a
R
I
I
a
I
I
V
a
V 2
2
'
'
'
' 




 





ou
onde os valores refletidos são:
Esta expressão é satisfeita pelo circuito equivalente a seguir, onde o
transformador ideal pode ser omitido. Notar que os valores reais no
secundário são Vs e Is.
• •

20. Impedância de carga no secundário refletida ao
primário
IS
.
VS
.
Zcarga
IS/a
.
aVS
.
a2
Zcarga=Zcarga

21. Modelo equivalente de um transformador real com o
secundário refletido no primário

22. Valores nominais de transformadores
(dados de placa)
• Tensões nominais
– Valores eficazes (rms)
– ex. 110 V/220 V, 13,8 kV/440 V
– Vnom1/Vnom2=anominal
• Potência nominal
– Potência aparente [VA]
– Correntes nominais obtidas a partir de Snom e Vnom

24. Tensão nominal no primário = 2400 V

26. anteriores:
continuando: