O documento discute como a programação funcional pode ser uma ferramenta poderosa para lidar com a complexidade de programas. Apresenta abstrações funcionais como monóides e mônadas que permitem dividir programas em partes menores e compô-los de forma previsível, levando à corretude por construção. Também discute como essas abstrações matemáticas promovem maior abstração no desenvolvimento de software.

1. OU COMO
PROGRAMAÇÃO FUNCIONAL É UMA ÓTIMA FERRAMENTA PARA CONTROLE
DE COMPLEXIDADE.
PROGRAMAS E FUNÇÕES
SOBRE
PENSANDO EM CORRETUDE,

2. Pessoas cometem erros
Programadores são pessoas
∴ Programadores cometem erros

3. Ferramentas e linguagens importam;

4. Ajudam a expressar, abstrair e construir.

5. Arthur Xavier
Estudante de Ciência da Computação;
Apaixonado por programação funcional;
Membro ativo da comunidade FP;
Desenvolvendo com Phil Freeman uma formalização
de interfaces de usuário declarativas com Comonads;

6. OU COMO
PROGRAMAÇÃO FUNCIONAL É UMA ÓTIMA FERRAMENTA PARA CONTROLE
DE COMPLEXIDADE.
PROGRAMAS E FUNÇÕES
SOBRE
PENSANDO EM ABSTRAÇÃO,

7. Outline
Por que programação funcional;
Abstrações funcionais;
Complexidade sem dificuldade:
1. Monóides;
2. Mônadas.

8. Corretude & Abstração

9. Corretude?

10. comando1();
comando2(); // mudança de estado
variável = comando3(); // estado privado
if (variável.atributo)
exceção!
envia_email(); // mudança de estado
lança_míssil();
// return variável;

11. Como garantir corretude dessa forma?

13. Linguagens convencionais
Semântica sequencial de transições de estado;
Divisão entre mundo das expressões vs. comandos;
Dificuldade de combinar programas;
Ausência de propriedades matemáticas.

14. Abstração?

15. Valores; (imutáveis)
Funções; (puras)

16. Funções são valores!

17. Funções de ordem superior!

18. // users = usernames.map(getAccount)
users.map(numberOfPosts).reduce(maximum, 0)
=
users.reduce(maximum ∘ numberOfPosts, 0)

19. // users = map(usernames, getAccount)
reduce(maximum, 0, map(numberOfPosts, users))
=
reduce(maximum ∘ numberOfPosts, 0, users)

20. HASKELL
-- users = map usernames getAccount
reduce maximum 0 (map numberOfPosts users)
=
reduce (maximum . numberOfPosts) 0 users

21. Composição.

22. Composição de funções ⇒ composição de programas.

23. Corretude ⟺ Abstração

24. Corretude por construção.

25. ~ Abstração ~

26. O que faz uma boa abstração?

27. Intuitividade & Universalidade

28. Matemática!

29. Álgebra abstrata & Teoria de categorias

30. MONÓIDES

31. Conjunto S com uma operação binária •, tal que
1. ∀a,b ∈ S : a•b ∈ S. (fechamento)
2. ∀a,b,c ∈ S : (a•b)•c = a•(b•c). (associatividade)
3. ∃e ∈ S : ∀a ∈ S : e•a = a•e = a. (identidade)

32. Acumulador com “elemento neutro”;

33. (a + b) + c = a + (b + c).
a + 0 = 0 + a = a.

34. (a × b) × c = a × (b × c).
a × 1 = 1 × a = a.

35. max(max(a, b), c) = max(a, max(b, c)).
max(a, 0) = max(0, a) = a. (a > 0)

36. Monóides são ubíquos.

37. Yorgey, B. A. (2012). Monoids: theme and variations (functional pearl).

38. connectionBuilder
.withHost("myhost.com")
.withRemote("remote.com")
.withAuth(PASSWORD)
.build()

39. recipe =
withHost("myhost.com")
+ withRemote("remote.com")
+ withAuth(PASSWORD)
build(recipe)

40. Mas e daí?
O que isso traz? O que isso abstrai?

41. Dividir para conquistar.

42. (a•b)•c
=
((a1
•a2
•a3
)•(b1
•b2
))•(c1
•c2
)
=
(((a11
•a12
)•a2
•(a31
•a32
• …))•(b1
•b2
))•(c1
•(c11
•c12
• …))

43. Paralelismo & Incrementalidade

44. (a•b)•c
=
((a1
•a2
•a3
)•(b1
•b2
))•(c1
•c2
)
=
(((a11
•a12
)•a2
•(a31
•a32
• …))•(b1
•b2
))•(c1
•(c11
•c12
• …))

45. HASKELL
class Monoid s where
(<>) :: s -> s -> s
mempty :: s

46. Mas e as leis?

47. HASKELL
(a <> b) <> c ≡ a <> (b <> c)
mempty <> a ≡ a
a <> mempty ≡ a

48. Não tem como garantir.
¯_(ツ)_/¯

49. HASKELL
data Add = Add Int
instance Monoid Add where
Add a <> Add b = Add (a + b)
mempty = Add 0
…
data Mult = Mult Int
instance Monoid Mult where
Mult a <> Mult b = Mult (a * b)
mempty = Mult 1

50. HASKELL
foldMap :: Monoid m => (a -> m) -> [a] -> m
foldMap f [] = mempty
foldMap f (a:as) = f a <> foldMap f as

51. HASKELL
reduce maximum 0 (map numberOfPosts users)
=
reduce (maximum . numberOfPosts) 0 users
≅
foldMap (Max . numberOfPosts) users

52. HASKELL
> foldMap (Add . numberOfPosts) [user1, user2, …]
Add 98
> foldMap (Max . numberOfPosts) [user1, user2, …]
Max 10
> foldMap (Min . numberOfPosts) [user1, user2, …]
Min 1
> foldMap (Max . numberOfPosts) []
Max (-9223372036854775808)

53. HASKELL
data Maybe a = Nothing | Just a
instance Monoid a => Monoid (Maybe a) where …
…
> foldMap (Just . Max . numberOfPosts) []
Nothing

54. Exemplo: builder

55. HASKELL
data Builder a = Builder (a -> a)
instance Monoid (Builder a) where
Builder f <> Builder g = Builder (f . g)
mempty = Builder id
build :: a -> Builder a -> a
build def (Builder builder) = builder def

56. HASKELL
conn :: Connection
conn = build defaultConnection recipe
where
recipe =
withHost "myhost.com"
<> withRemote "remote.com"
<> withAuth Password

57. Disjunção de predicados;
Conjunção de predicados;
Conjuntos com união;
Composição de opções;
Combinação de regras;
Interseção de formas bidimensionais;
Funções que retornam monóides;
Combinação de máquinas de estado;

58. MÔNADAS

59. Pra quê?

60. Exemplo: logging

61. HASKELL
add1 :: Int -> (Int, String)
add1 x = (x + 1, "+1")
mul3 :: Int -> (Int, String)
mul3 x = (x * 3, "*3")
-- deseja-se
add1 30 ?? mul3 ?? add1 = (94, "+1*3+1")
-- mas o que é (??)

62. HASKELL
add1 :: Int -> (Int, String)
add1 x = (x + 1, "+1")
mul3 :: Int -> (Int, String)
mul3 x = (x * 3, "*3")
-- ou ainda
do
x <- add1 30
y <- mul3 x
add1 y

63. HASKELL
add1 :: Int -> (Int, String)
add1 x = (x + 1, "+1")
mul3 :: Int -> (Int, String)
mul3 x = (x * 3, "*3")
-- deseja-se
add1 30 ?? mul3 ?? add1 = (94, "+1*3+1")
-- mas o que é (??)

64. HASKELL
(??) :: (Int, String) -> (Int -> (Int, String)) -> (Int, String)

65. Produção de contexto na saída;

66. Impureza na saída;

67. Sequencialidade.

68. Tipo m com duas operações pure e bind
pure :: a -> m a
bind :: m a -> (a -> m b) -> m b
(>>=) = bind

69. HASKELL
class Monad m where
(>>=) :: m a -> (a -> m b) -> m b
pure :: a -> m a

70. HASKELL
(>=>) :: (a -> m b) -> (b -> m c) -> (a -> m c)
f >=> g = (f x) >>= g

71. HASKELL
(f >=> g) >=> h ≡ f >=> (g >=> h)
pure >=> f ≡ f
f >=> pure ≡ f

72. HASKELL
(a <> b) <> c ≡ a <> (b <> c)
mempty <> a ≡ a
a <> mempty ≡ a

73. “A monad is just a monoid in the category of endofunctors,
what’s the problem?”

74. Writer: logging
a -> (b, String)

75. HASKELL
data Writer a = Writer (a, String)
instance Monad Writer where
pure a = Writer (a, "")
Writer (a, s) >>= f = Writer (b, s ++ s2)
where
Writer (b, s2) = f a

76. Writer: logging
Monoid t => a -> (b, t)

77. HASKELL
data Writer t a = Writer (a, t)
instance Monoid t => Monad (Writer t) where
pure a = Writer (a, mempty)
Writer (a, t) >>= f = Writer (b, t <> t2)
where
Writer (b, t2) = f a

78. HASKELL
add1 :: Int -> Writer String Int
add1 x = Writer (x + 1, "+1")
mul3 :: Int -> Writer String Int
mul3 x = Writer (x * 3, "*3")
add1 30 >>= mul3 >>= add1 = (94, "+1*3+1")

79. HASKELL
add1 :: Int -> Writer String Int
add1 x = Writer (x + 1, "+1")
mul3 :: Int -> Writer String Int
mul3 x = Writer (x * 3, "*3")
do
x <- add1 30
y <- mul3 x
add1 y

80. HASKELL
tell :: Monoid t => t -> Writer t ()
tell t = Writer ((), t)
add1 x = do { tell "+1"; pure (x + 1) }
mul3 x = do { tell "*3"; pure (x * 3) }
do
x <- add1 30
y <- mul3 x
add1 y

81. State: estado
a -> (s -> (b, s))
≅
(a, s) -> (b, s)

82. HASKELL
data State s a = State (s -> (a, s))
instance Monad (State s) where …
put :: s -> State s ()
put s = _ -> ((), s)
get :: State s s
get = s -> (s, s)
modify :: (s -> s) -> State s ()
modify f = s -> ((), f s)

83. HASKELL
put :: s -> State s ()
get :: State s s
modify :: (s -> s) -> State s ()
…
add1 x = do
modify (log -> log <> "+1")
pure (x + 1)
mul3 x = do
modify (log -> log <> "*3")
pure (x * 3)

84. Maybe: falha
a -> Maybe b

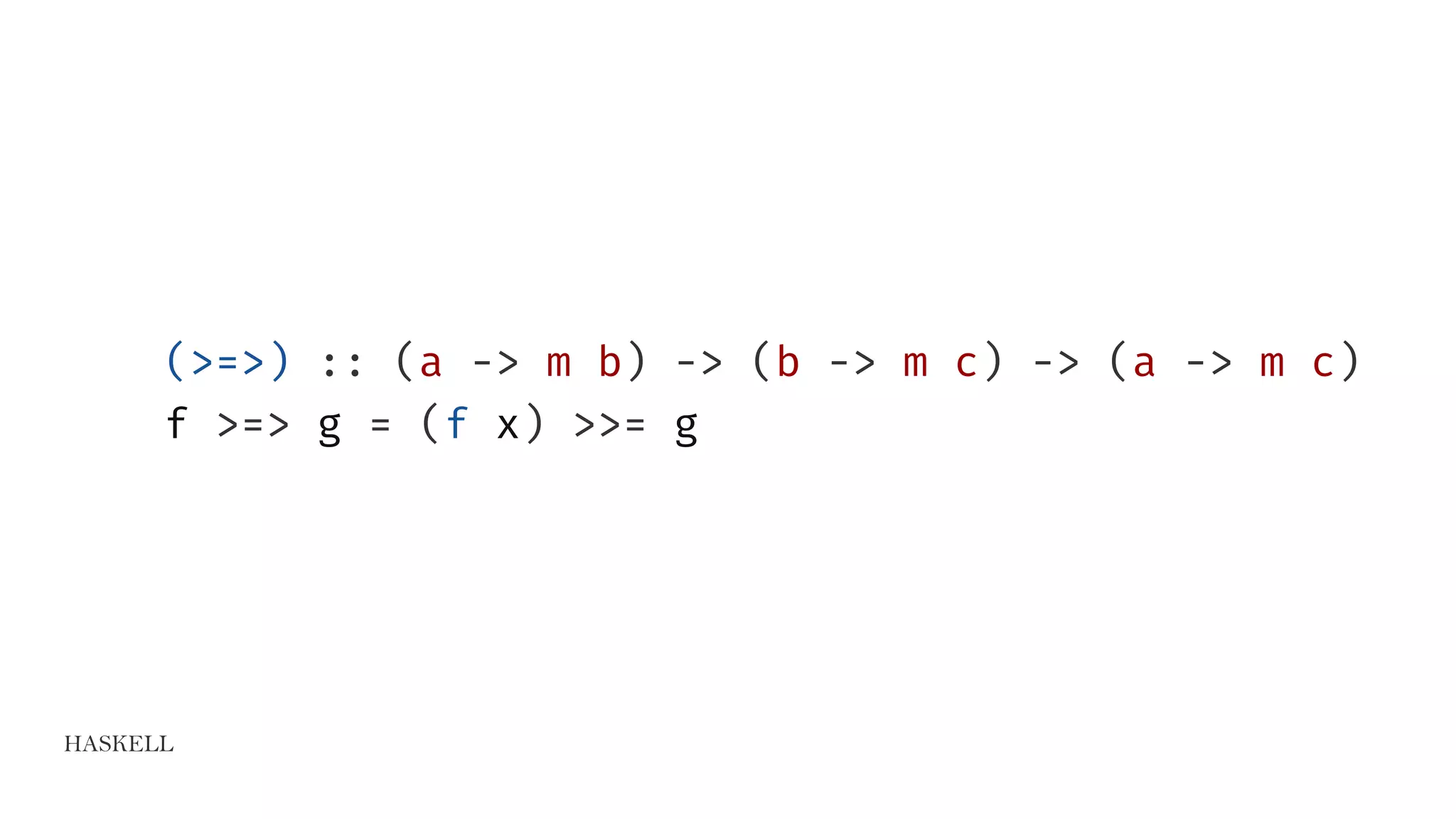
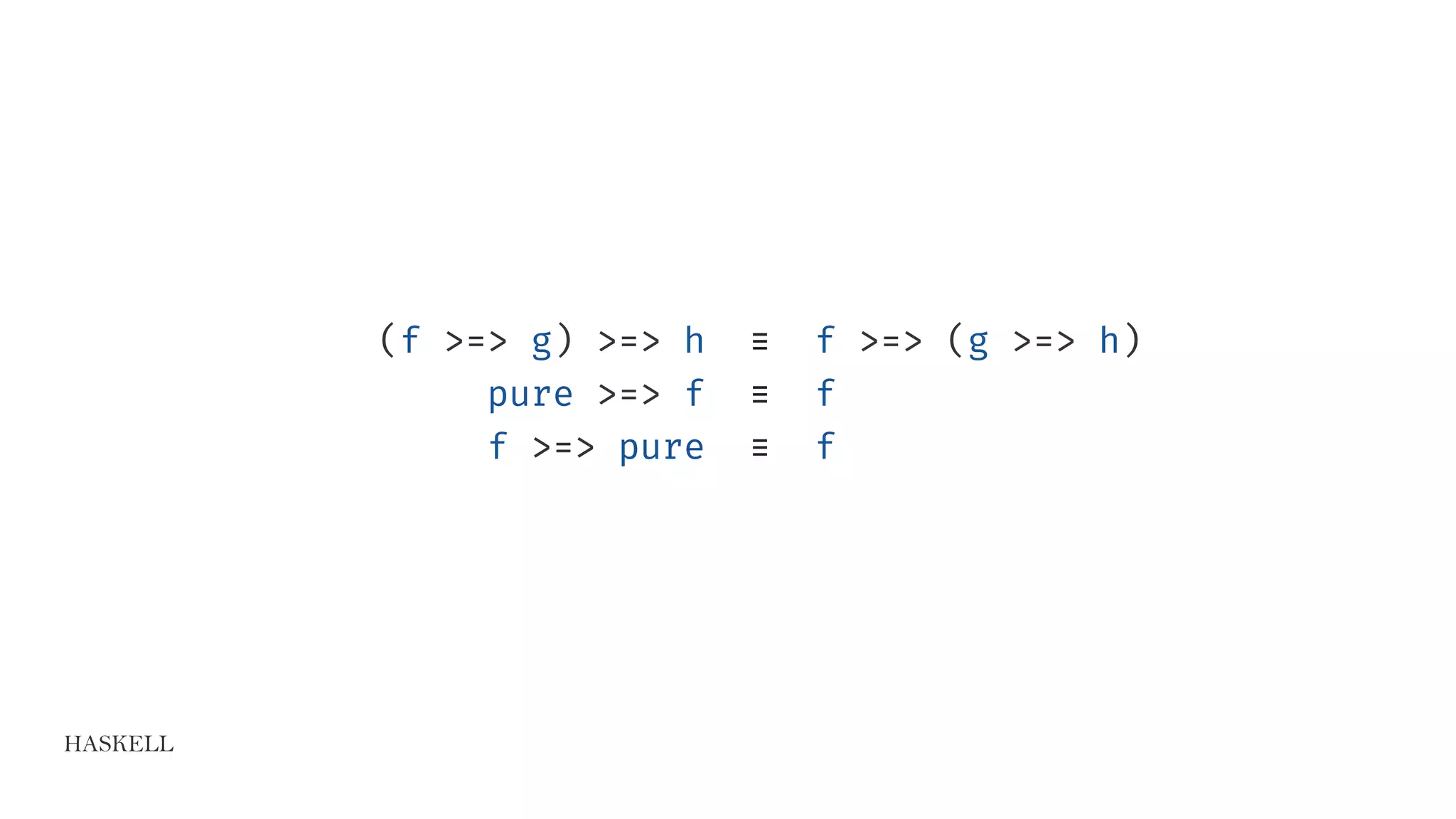
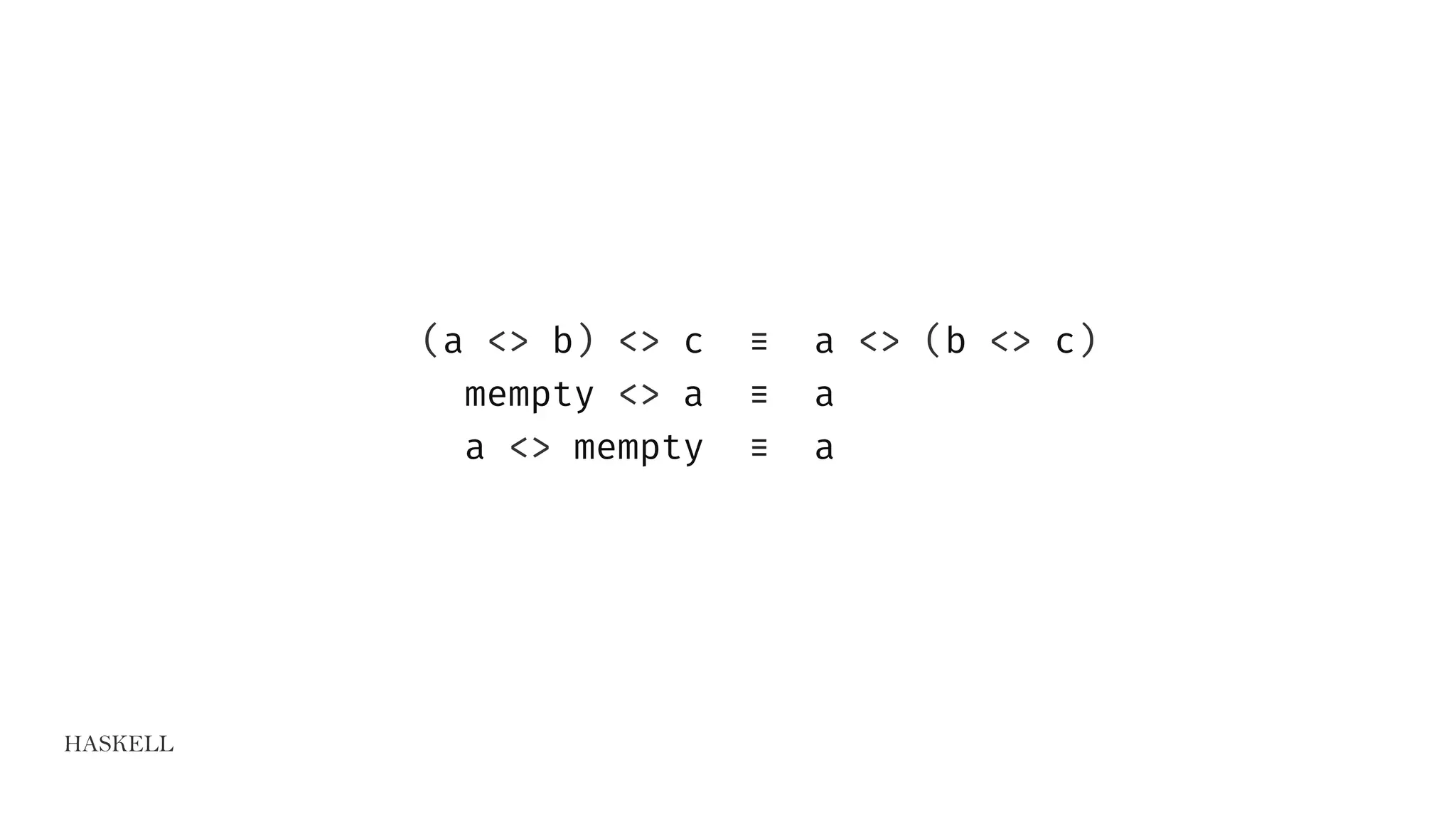
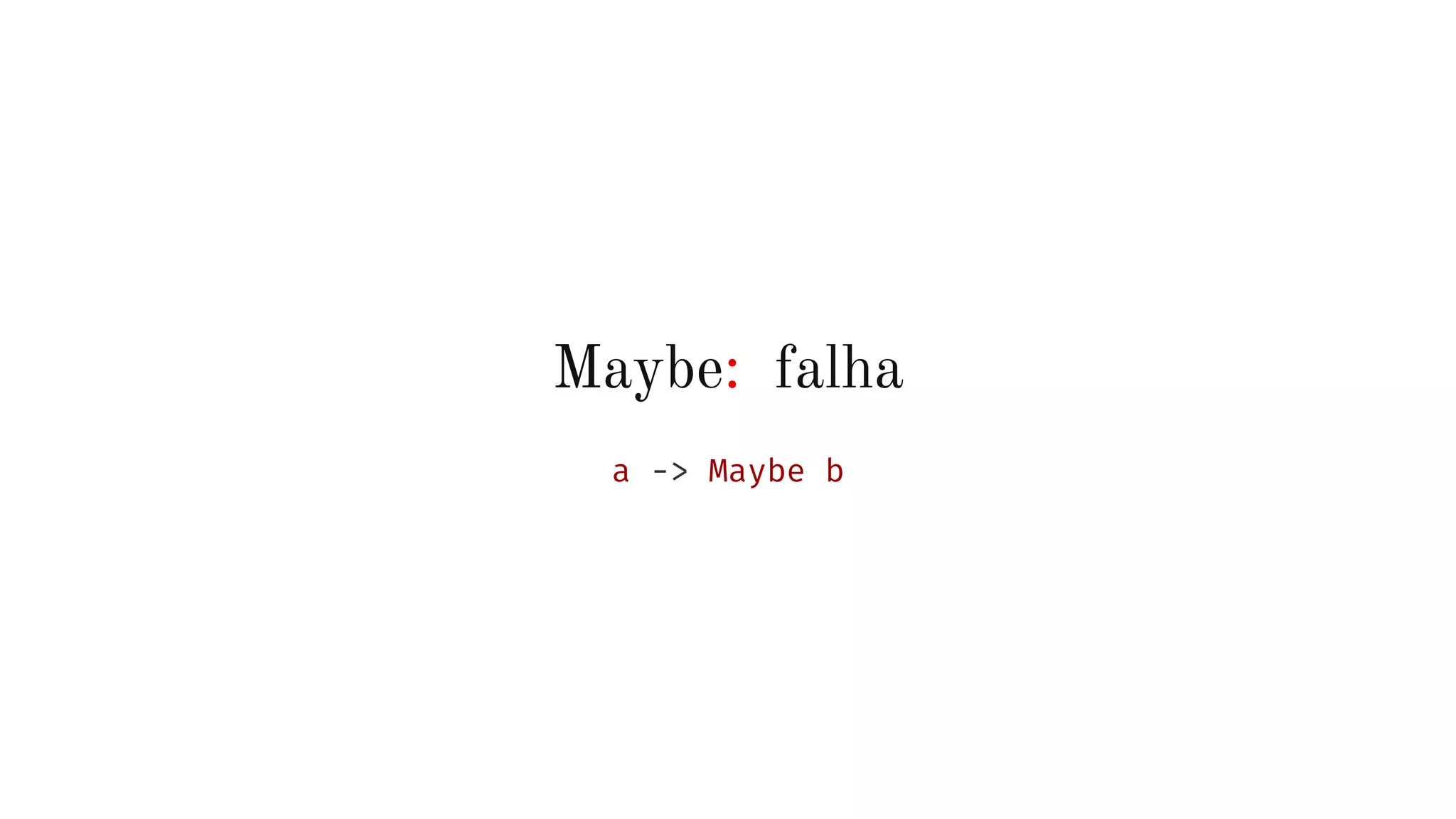
85. HASKELL
data Maybe a = Nothing | Just a
instance Monad Maybe where …
head :: [a] -> Maybe a
…
tryGetLastPhoto username = do
user <- tryGetUser username
photos <- tryGetPhotos user
head photos

86. Padrão universal quando se trata de computações.

87. Reader: ambiente global
a -> (r -> b)
≅
(a, r) -> b

88. List: não-determinismo
a -> [b]

89. Dist: não-determinismo com probabilidades
a -> [(b, Float)]

90. Parser: parsing…
a -> (String -> [(b, String)])
≅
(a, String) -> [(b, String)]

91. Cont: continuações
a -> ((b -> r) -> r)
≅
(a -> r) -> (b -> r)

92. IO: efeitos colaterais
a -> (RealWorld -> (b, RealWorld))
≅
(a, RealWorld) -> (b, RealWorld)

93. Computações & Algoritmos

94. Sequencialidade;

95. Do ponto de vista interno,
permitem efeitos colaterais;

96. Sequência de computações são executadas
e têm seus resultados e efeitos combinados no final;

97. Mônadas abstraem programas!

98. Muitas abstrações funcionais são sobre composição.

99. Leis + composição ⇒ corretude por construção.

100. Mais?

101. Funtores aplicativos;
Free monad;
Monad transformers;
Comônadas;
Lentes;
Categorias;
Contêineres indexados;
Esquemas de recursão;

102. λ
@arthurxavierx @arthur-xavier