O documento discute as características da linguagem de programação Haskell, destacando sua pureza funcional, tipagem estática e forte, e avaliação preguiçosa. Apresenta conceitos como funções de ordem superior, currying, monads e tipos de dados, além de exemplos práticos para ilustrar esses conceitos. A linguagem é enfatizada como uma ferramenta poderosa na programação funcional, aplicável na indústria.

1. HASKELL

2. Por quê
Haskell?

3. Por quê Haskell?
Programação funcional conquista a indústria

4. Por quê Haskell?
Haskell: exemplo mais puro de
(um certo estilo bem poderoso de)
programação funcional

5. Características

6. Linguagem funcional pura
● Variáveis imutáveis
● Definições ao invés de atribuições
● Similar à matemática

7. > let n = 3
> n
3

8. Linguagem funcional pura
● Funções são “cidadãs de primeira classe.”
● Lambdas (funções anônimas).

9. > (n -> n<5) 3
True
> (n -> n<5) 6
False

10. Linguagem funcional pura
● Funções podem ser passadas como
argumentos.

11. > let less n p = n < p
> let lessThan5 n = less n 5
> filter lessThan5 [1,2,3,4,5,6]
[1,2,3,4]

12. Linguagem funcional pura
● Funções podem ser retornadas… em certo
sentido.

13. > let lessThan p = n -> n<p
> let lessThan5 = lessThan 5
> lessThan5 3
True
> lessThan5 7
False

14. Linguagem funcional pura
● Currying: passar menos argumentos à chamada
resulta em uma nova função.

15. > let isPositive = less 0
> let positives = filter isPositive
> positives [1,-1,0,-2,4,-8]
[1,4]

16. Linguagem funcional pura
● Operadores são funções.

17. > 3 + 2
5
> (+) 3 2
5
> let add = (+)
> add 3 2
5
> 3 `add` 2
5

18. Linguagem funcional pura
● Sem efeitos colaterais.
● Variáveis não mudam
● Mas definições podem mudar em escopos
diferentes
● let cria escopos.

19. > let n = 2
> n
2
> let n = 3
> n
3

20. Linguagem funcional pura
● Descrição, mas não execução, de operações
entrada e saída.
● Execução de operações de entrada e saída fica
a cargo do runtime.
● Operações de entrada e saída são descritas
pelo tipo IO, que é uma...

21. MÔNADA

23. Mônadas
"a monad is a monoid in the
category of endofunctors"

24. Linguagem tipada
● Estaticamente tipada: tipos de expressões já
estão definidos em tempo de compilação.
● Fortemente tipada: sem coerções.
● Tipagem implícita.

25. > let n = True
> :t n
n :: Bool
> n && False
False
> n && 0
<interactive>:67:6:
No instance for (Num Bool) arising from
the literal ‘0’
In the second argument of ‘(&&)’, namely
‘0’
In the expression: n && 0
In an equation for ‘it’: it = n && 0

26. Linguagem tipada
● Tipos de funções
● Tipos parametrizáveis
● Variáveis de tipo

27. > :t (&&)
(&&) :: Bool -> Bool -> Bool
> :t (&&) True
(&&) True :: Bool -> Bool
> :t filter
filter :: (a -> Bool) -> [a] -> [a]
> :t filter ((&&) True)
filter ((&&) True) :: [Bool] -> [Bool]

28. > let l = [True, False, False]
> :t l
l :: [Bool]
> let s = "Hello"
> :t s
s :: [Char]
> let m = Just True
> :t m
m :: Maybe Bool
> let t = (True, 'a', "one string")
> :t t
t :: (Bool, Char, [Char])

29. > :t [True]
[True] :: [Bool]
> :t []
[] :: [t]
> :t Just 'a'
Just 'a' :: Maybe Char
> :t Nothing
Nothing :: Maybe a

30. Linguagem preguiçosa
● Avaliação preguiçosa (“lazy evaluation”).
● Cálculo de valores é postergado até serem
realmente necessários.

31. > [1..5]
[1,2,3,4,5]
> let l = [1..]
> l !! 0
1
> l !! 5
6
> l !! 300000
300001
> length l
^CInterrupted.

32. > let n = 1
> let n = n+1
> n
*** Exception: <<loop>>

33. > let n = 2
> n + (2 :: Integer)
4
> :t n + (2 :: Integer)
n + (2 :: Integer) :: Integer
> n + (2.0 :: Float)
4.0
> :t n + (2.0 :: Float)
n + (2.0 :: Float) :: Float
> (2 :: Integer) + (2.0 :: Float)
<interactive>:26:19:
Couldn't match expected type ‘Integer’ with actual type ‘Float’
In the second argument of ‘(+)’, namely ‘(2.0 :: Float)’
In the expression: (2 :: Integer) + (2.0 :: Float)
In an equation for ‘it’: it = (2 :: Integer) + (2.0 :: Float)

34. > :t n
n :: Num a => a

35. > [1..] !! 100
101
> zipWith (+) [1, 2, 3] [2, 4, 1]
[3,6,4]
> 1 : []
[1]
> 1 : [2, 3, 4]
[1,2,3,4]

36. > let what = 1 : zipWith (*) what [1..]
> what !! 0
1
> what !! 1
1
> what !! 2
2

37. > let what = 1 : zipWith (*) what [1..]
> what !! 0
1
> what !! 1
1
> what !! 2
2
> what !! 3
6
> what !! 4
24
> what !! 5
120
> what !! 6
720

38. > let wut = 1 : 1 : zipWith (+) wut (tail wut)
> wut !! 0
1
> wut !! 1
1

39. > let wut = 1 : 1 : zipWith (+) wut (tail wut)
> wut !! 0
1
> wut !! 1
1
> wut !! 2
2
> wut !! 3
3
> wut !! 4
5
> wut !! 5
8
> wut !! 6
13

40. > undefined
*** Exception: .undefined
> (1, undefined)
(1,*** Exception: .undefined
> fst (1, undefined)
1

41. Linguagem fortemente tipada
● System F.
● Sistema de tipos extremamente poderoso.
● Não só protege como facilita modelagem.
● “Making illegal states unrepresentable”

42. Linguagem fortemente tipada
● Sum types
● Product types

43. > data EstadoSemaforo = Verde | Amarelo | Vermelho deriving (Show, Eq)
> let podePassar es = es /= Vermelho
> podePassar Verde
True
> podePassar Amarelo
True
> podePassar Vermelho
False
> Verde
Verde

44. > data Casa = Endereço { rua :: String, numero :: Integer } deriving (Show, Eq)
> let e = Endereço "Rua Jacó Velosino" 390
> rua e
"Rua Jac243 Velosino"
> numero e
390

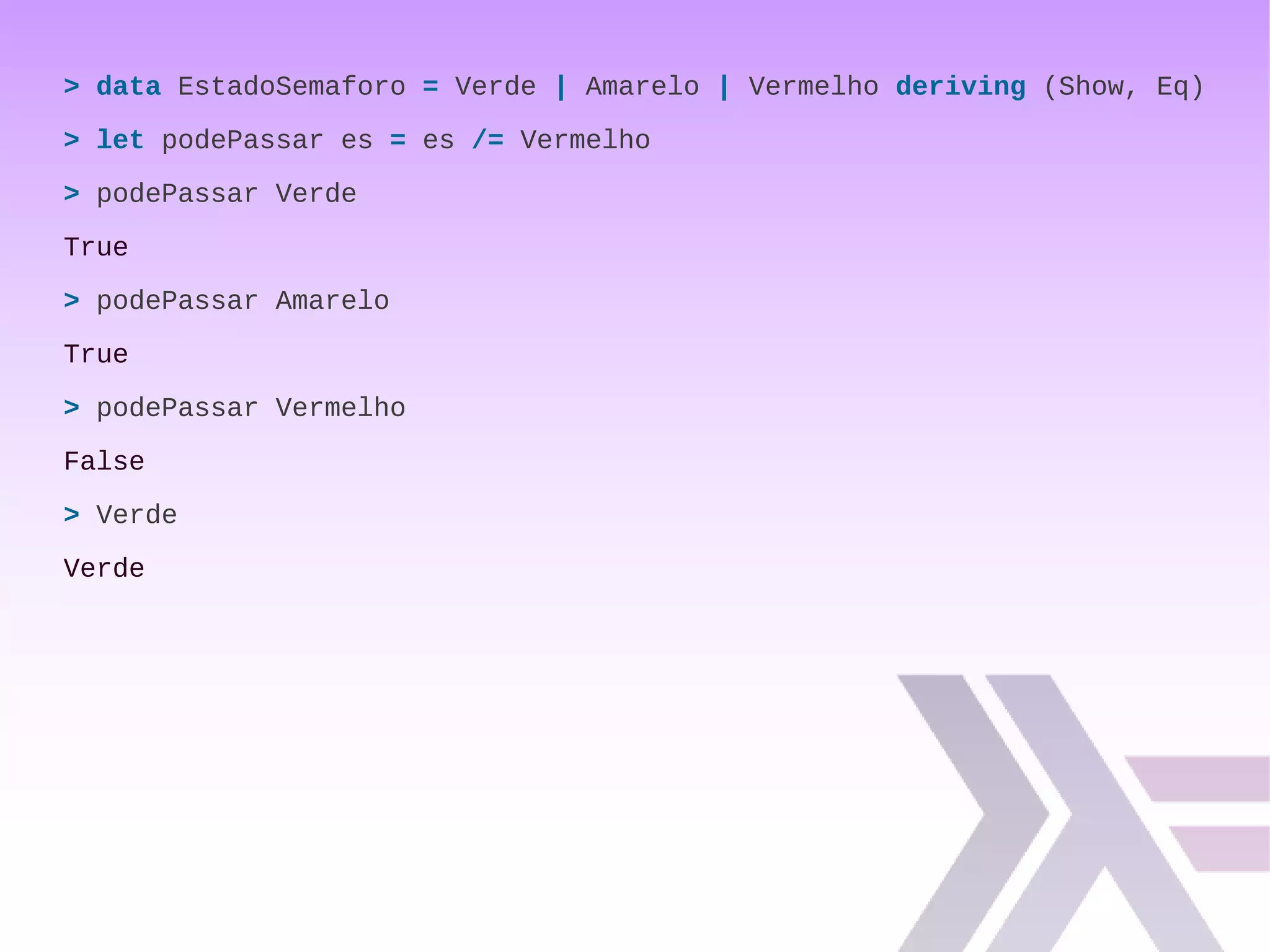
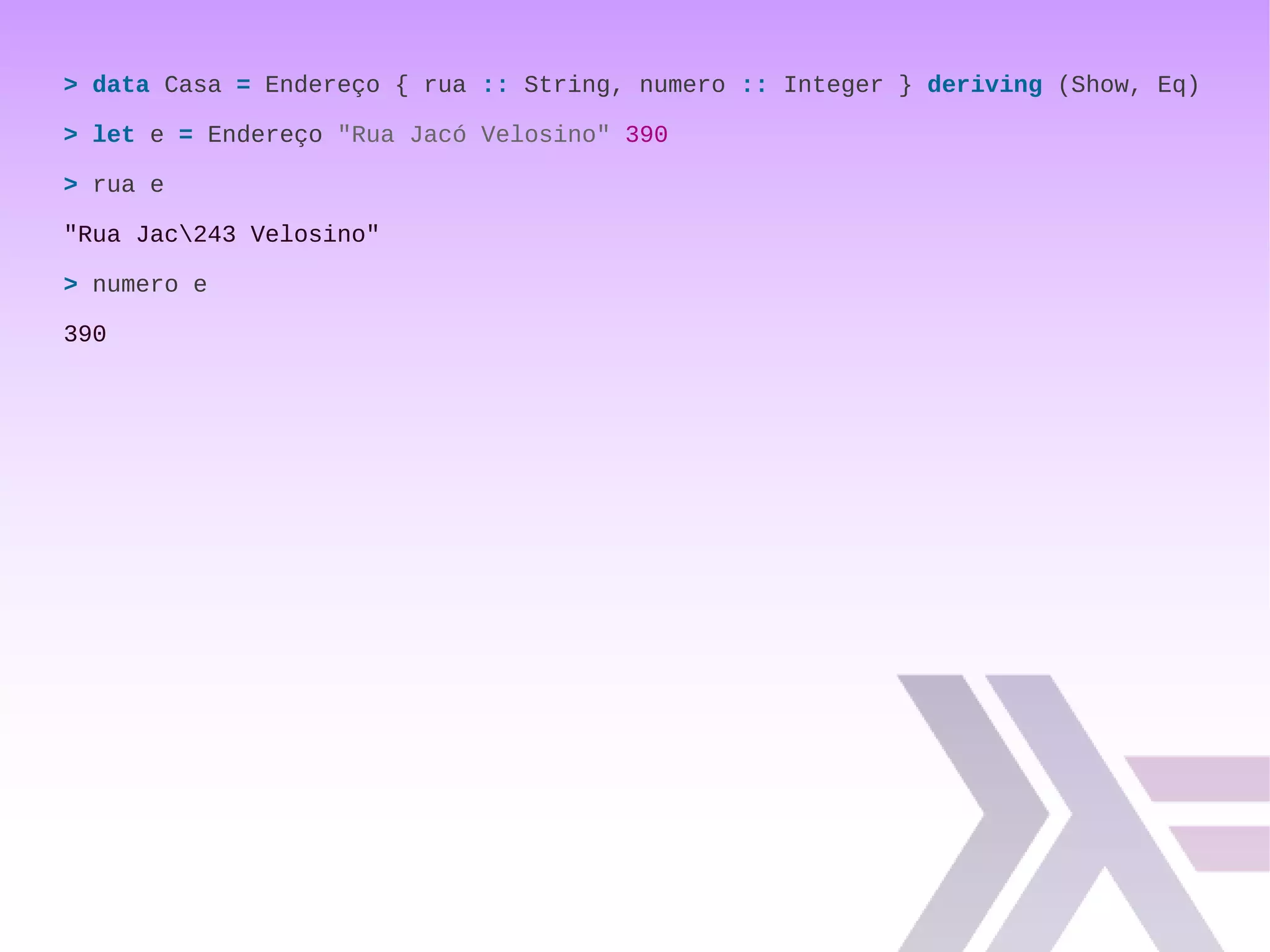
45. data Maybe a = Just a | Nothing
data Either a b = Left a | Right b
data [a] = [] | a : [a]

46. Controle de fluxo
● If then else
● Pattern matching
● Guardians
● Recursão
● Folding/mapping/filtering etc.

47. factorial n =
if n < 1 then 1
else n * (factorial $ n-1)

48. factorial n =
if n < 1 then 1
else n * (factorial $ n-1)

49. factorial n - 1 == (factorial n) - 1
factorial $ n - 1 == factorial (n-1)

50. factorial n
| n < 0 = 1
| n == 0 = 1
| n == 1 = 1
| otherwise = n * (factorial $ n - 1)

51. factorial 0 = 1
factorial n = n * (factorial $ n - 1)

52. factorial n =
foldl (*) 1 [1..n]

53. flist = 1 : zipWith (*) flist [1..]
factorial n = flist !! n