1. A introdução apresenta programação funcional e o autor Arthur Xavier.
2. Os benefícios da programação funcional incluem previsibilidade, testabilidade, facilidade de raciocínio e simplicidade.
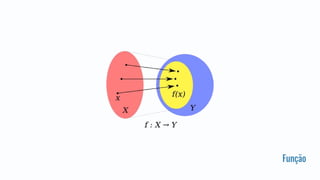
3. O documento discute conceitos como funções puras, imutabilidade, tipos, composição e recursividade.




![function squareArrayImperative(arr) {
let result = [];
for (let i = 0; i < arr.length; i++) {
result.push(arr[i] ** 2);
}
return result;
}
Programação imperativa](https://image.slidesharecdn.com/workshop-introducaoaprogramacaofuncionaltipada-170624030206/85/Programacao-funcional-tipada-uma-introducao-5-320.jpg)





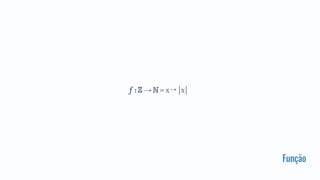


![(Elm) Funções
squareList : List Int -> List Int
squareList l =
case l of
[] -> []
x :: xs -> x^2 :: squareList xs
sumList : List Int -> Int
sumList l =
case l of
[] -> 0
x :: xs -> x + sumList xs](https://image.slidesharecdn.com/workshop-introducaoaprogramacaofuncionaltipada-170624030206/85/Programacao-funcional-tipada-uma-introducao-15-320.jpg)





![Função pura
function appendToArray(array, x) {
return [ ...array, x ];
}](https://image.slidesharecdn.com/workshop-introducaoaprogramacaofuncionaltipada-170624030206/85/Programacao-funcional-tipada-uma-introducao-21-320.jpg)
![(Elm) Função pura
appendToList : List Int -> Int -> List Int
appendToList list x = list ++ [x]](https://image.slidesharecdn.com/workshop-introducaoaprogramacaofuncionaltipada-170624030206/85/Programacao-funcional-tipada-uma-introducao-22-320.jpg)

![Função pura
const square = x => x*x;
const add = (a, b) => a + b;
function sumOfSquares(array) {
return array
.map(square)
.reduce(add, 0);
}
console.log(sumOfSquares([2, 3, 5]));](https://image.slidesharecdn.com/workshop-introducaoaprogramacaofuncionaltipada-170624030206/85/Programacao-funcional-tipada-uma-introducao-24-320.jpg)






![Função de alta ordem
map : (a -> b) -> List a -> List b
map f l =
case l of
[] -> []
x :: xs -> f x :: map f xs](https://image.slidesharecdn.com/workshop-introducaoaprogramacaofuncionaltipada-170624030206/85/Programacao-funcional-tipada-uma-introducao-31-320.jpg)
































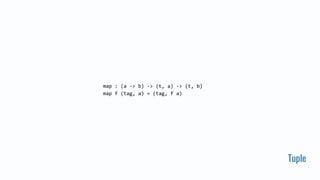
![List
map : (a -> b) -> List a -> List b
map f list =
case list of
[] -> []
x :: xs -> f x :: map f list](https://image.slidesharecdn.com/workshop-introducaoaprogramacaofuncionaltipada-170624030206/85/Programacao-funcional-tipada-uma-introducao-65-320.jpg)









