O documento aborda a programação funcional, destacando sua história desde o cálculo lambda e a criação da linguagem Lisp até conceitos como imutabilidade, recursividade e avaliação preguiçosa. A programação funcional é apresentada como um paradigma que foca em funções e transformações de dados, diferindo dos paradigmas imperativos e orientados a objetos. Exemplos práticos em Haskell ilustram características como funções de alta ordem, currying e compreensão de listas.

1. PROGRAMAÇÃO
FUNCIONAL
1
@NatanJMai

2. HISTÓRIA
2
1930 1950 1970 - 1980
Criação do Cálculo
Lambda, por
Alonzo Church.
Uma maneira de
expressar
computações na
forma de funções.
Criação da
linguagem LISP,
baseada no Cálculo
Lambda, por John
McCarty.
Linguagem muito
utilizada até hoje.
David Turner
desenvolve
algumas
linguagens,
empregando lazy
evaluation.

3. O QUE É?
Programação Funcional
❏ Paradigma diferente que trata
todas as computações em forma
de funções. Enfatiza o uso de
funções e evita o uso de
variáveis e estados.
❏ Experiência em outros
paradigmas não facilita tanto a
programação funcional.
Outros
paradigmas:
● Imperativa
● Procedural
● Lógica
● Orientada a objetos.
3

4. O QUE É?
Programação Funcional
❏ Diferente do paradigma
imperativa, aqui não escrevemos
“como fazer algo”, mas sim “o
que queremos fazer”
Outros
paradigmas:
● Imperativa
● Procedural
● Lógica
● Orientada a objetos.
4
- Funcional: Funções, expressões, recursividade.
- Imperativa: Atribuições, variáveis, estados.
- O. Objetos: Objetos, classes, métodos.

5. FUNCIONAL vs IMPERATIVA
❏ Funções são as principais formas de transformar
dados;
❏ Ao contrário da imperativa, onde valores podem ser
alterados, na funcional os valores são imutáveis
(immutable state).
❏ Sem loops (while, for, etc) e sim com recursão.
Recursividade é a principal forma de iteração entre
algo.
5

6. FUNCIONAL vs IMPERATIVA
6
Funcional Imperativa
Foco
Qual informação é desejada
e quais transformações são
necessárias
Sequência de passos e
tarefas para obter as
informações.
Estados Não existe. É a base da programação.
Ordem
Execução
Baixa importância. É a base da programação.
Fluxos.
Chamadas de funções,
recursividade.
Loops, if’s.

7. Sequência:
- Avaliação preguiçosa
- Funções Anônimas
- Compreensão de listas
- Funções de primeira classe
- Funções de alta ordem
- Currying
- Estados imutáveis.
CARACTERÍSTICAS
7

8. AVALIAÇÃO PREGUIÇOSA
8

9. AVALIAÇÃO PREGUIÇOSA
❏ Uma expressão / função não é valorada caso não seja
utilizável durante o programa. Assim, os valores que
não serão utilizados, não serão computados.
- Ex.: Imagine passar 3 parâmetros para uma
função, mas que conforme a sequência precise
utilizar apenas 2 deles. Em funções em linguagens
como C, Java, os 3 seriam computados.
9

10. AVALIAÇÃO PREGUIÇOSA
❏ O principal ganho com lazy evaluation além do
desempenho, é a habilidade de criarmos estruturas
de dados infinitas.
- Como trabalhar facilmente com uma lista infinita?
10
:|

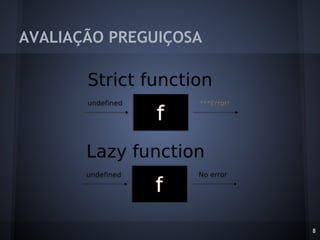
11. AVALIAÇÃO PREGUIÇOSA
❏ Exemplo de trabalho com uma lista infinita em Haskell:
> [1..]
> [1, 2, 3, 4, ..]
> take 10 [1..]
> [1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ..]
> take 5 [2, 4..]
> [2, 4, 6, 8, 10]
11

12. AVALIAÇÃO PREGUIÇOSA
12
LAZINESS IS
NOT ALWAYS
BAD.

13. FUNÇÕES ANÔNIMAS
13
❏ Funções não necessitam de declaração e
especificação. Não precisam nem mesmo de um
nome, por isso são conhecidas como anônimas. Já não
são exclusividade de linguagens funcionais.
Python:
> f = lambda x: x * x
> f (3)
> 9
Haskell:
x -> x * x
> (x -> x * x) 3
> 9

14. COMPREENSÃO DE LISTAS
14
❏ É uma forma muito simples de trabalhar com listas de
dados, tendo em vista que é baseado na notação de
definição de conjunto.
Ex.:
➔ S = { x² | x pertença aos números naturais }
➔ Haskell:
> [ x ^ 2 | x <- [0..]]

15. COMPREENSÃO DE LISTAS
15
❏ Alguns exemplos da utilidade da compreensão de
listas em Haskell.
Ex.:
Soma dos quadrados dos 10 primeiros números > 2.
> sum [ x ^ 2 | x <- take 10 [3..]]
> 645

16. COMPREENSÃO DE LISTAS
16
Ex .:
Quadrado dos 10 primeiros ímpares a partir de 3.
> [x ^ 2 | x <- filter odd (take 10 [3..])]
> [ 3², 5², 7², 9², 11²]
> [ 9, 25, 49, 81, 121 ]

17. FUNÇÕES DE PRIMEIRA CLASSE
17
❏ Possibilidade de armazenar funções em variáveis.
❏ Passagens de funções como parâmetro, para outras
funções.
- De forma geral, as funções de primeira classe são
tratadas, criadas e utilizadas em qualquer lugar,
assim como valores normais.

18. FUNÇÕES DE PRIMEIRA CLASSE
18
❏ Passagens de funções como parâmetro, para outras
funções.
- Ex .: (Haskell)
> map flisol [2, 4, 6, 8]
> [4, 8, 12, 16]
> :t map
> map :: (a -> b) -> [a] -> [b]
> flisol :: Float -> Float
> flisol x = (x / 2) * 4
> :t flisol
> flisol :: Float -> Float

19. FUNÇÕES DE ALTA ORDEM
19
❏ Função que recebe funções como parâmetro.
❏ Função que retorna uma outra função.
> map flisol [2, 4, 6, 8]
> [4, 8, 12, 16]
> :t map
> map :: (a -> b) -> [a] -> [b]
Função
- Importante na definição
do que de fato “é”.
- Podemos passar
qualquer função para
map.
Parâmetro
Saída

20. CURRYING
20
❏ Técnica de transformação de uma função com
múltiplos parâmetros em uma cadeia de funções com
apenas um parâmetro.
> function f(x, y) {
return x + y;
}
> function g(x, y) {
return function (y){
return x + y;
};
}
- f(x, y) == g(x, y)

21. CURRYING
❏ Em Haskell, todas as funções são de apenas 1
parâmetro, o que ocorre é a utilização da técnica de
Currying.
21
> max 4 5
> 5
> (max 4) 5
> 5
> div :: (Floating a) => a -> a
> div = ( / 10)
> (div) 100
> 10
Com Currying, é criado uma função que recebe 4 e retorna uma
função que espera um parâmetro, neste caso, o 5.

22. ESTADOS IMUTÁVEIS
❏ Não é possível alterar o estado de algo, embora
possamos criar um novo estado a partir do mesmo.
❏ Excelente vantagem quando trabalhado em softwares
que necessitam de concorrência e paralelismo.
22
> fl = 2
> fli = fl + 1
> fli = 3
CORRETO!.
> fl = 2
> fl = flisol + 1
ERRO!.

23. CURIOSIDADES (Erlang)
- github.com/erlang/otp
- www.erlang.org/
- Utilizada amplamente no setor de telecomunicações,
além de serviços em banco de dados.
23
- Amazon
- Yahoo
- Facebook (Chat)
- WhatsApp
- Ericsson.

24. CURIOSIDADES (Scala)
- github.com/scala/scala
- www.scala-lang.org/
- Um ponto forte é a criação de linguagens de domínio
específico (DSL), como a Rogue.
24
- Linkedin
- Twitter
- Foursquare
- Sony

25. - www.haskell.org/
- www.haskell.org/community
- Finanças, web startups, design de hardware, e até
fabricantes de cortadores de grama.
CURIOSIDADES (Haskell)
25
- Facebook
- Google
- Intel
- etc.

26. - Utilizado como linguagem de extensão do software de
CAD AutoCAD, desenvolvido pela AutoDesk.
- Lisp foi utilizado para desenvolver o primeiro sistema
computacional de matemática simbólica, o Macsyma.
CURIOSIDADES (Lisp)
26
- AutoCAD
- Emacs
- Orbitz
- etc.
LISP

27. EXEMPLOS
❏ Soma dos números ímpares de 0 a 300.
Haskell
27
> sum (filter odd [0..300])
> 22500
Odd - Ímpar (bool)
Sum - Soma a lista
Filter - Filtro

28. EXEMPLOS
❏ Números entre 0 e 100 divisíveis por 3.
Haskell
28
> filter p [1..100]
> where p x =
> x `mod` 3 == 0
>
[3,6,9,12,15,18,21,24,27,30,33,
36,39,42,45,48,51,54,57,60,63,6
6,69,72,75,78,81,84,87,90,93,96
,99]

29. EXEMPLOS
❏ Soma dos 5 primeiros números maiores que 0 tal que o
seu quadrado seja maior que 1000.
Haskell
29
> sum (take 5 [x | x <- [0..], x ^ 2 > 1000])
> 170

30. EXEMPLOS
❏ Fatorial
Haskell
30
> fat :: (Num a, Eq a) => a -> a
> fat 0 = 1
> fat x = x * fat (x - 1)
> fat 5
> 120

31. EXEMPLOS
❏ (x, y, z) tal que (x, y, z) <= 50 e
2x + y - z = 1
3x - y + 2z = 7
x + y + z = 6
31
> [(x, y, z) | x <-[0..50], y <- [0..50], z <-[0..50],
(2 * x + y - z) == 1,
(3 * x - y + 2 * z) == 7,
(x + y + z) == 6]
> [(1, 2, 3)]
Haskell

32. MAIS?
32
❏ Learn You a Haskell
(learnyouahaskell.com)
❏ Functional programming in Scala
(Coursera, Martin Odersky) -
Desenvolvedor da linguagem.
❏ Diversos projetos no Github.

33. - Natan J. Mai
- Estudante de Ciência da Computação, UFFS.
- Estudo por conta própria alguns assuntos do meu
interesse. Linguagem de programação acabou se tornando
um deles.
SOBRE
33
- natan.mai@hotmail.com
- natanmai2@gmail.com
@NatanJMai
@NatanJMai

34. 34
“Uma linguagem que não afeta a
maneira que você pensa sobre
programação, não vale a pena ser
aprendida”
Alan Perlis