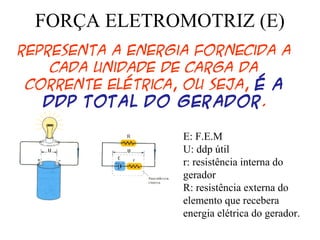
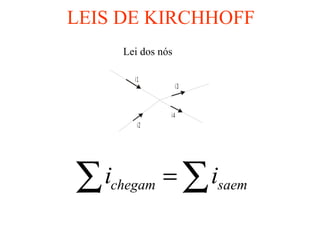
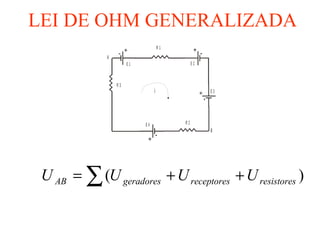
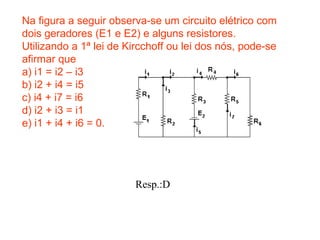
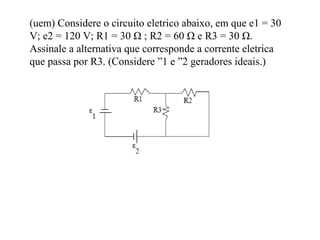
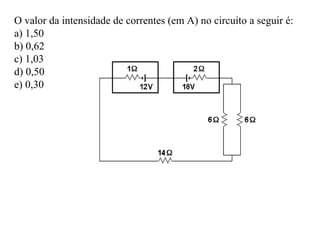
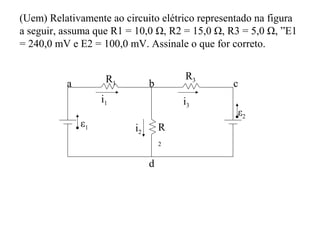
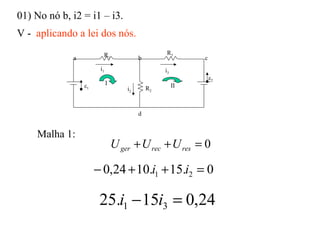
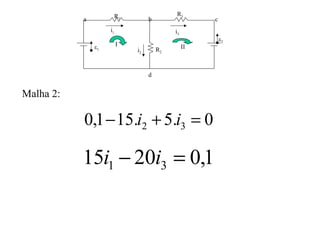
O documento descreve conceitos básicos sobre geradores e receptores elétricos, incluindo suas representações simbólicas, equações e leis de Kirchhoff. Explica que um gerador transforma energia em energia elétrica e um receptor transforma energia elétrica em outra forma de energia, além de definir força eletromotriz e força contra-eletromotriz.

2. GERADOR ELÉTRICO
Dispositivo que transforma uma certa forma
de energia em energia elétrica.

3. SÍMBOLO DO GERADOR
E
i
+
-r
O gerador pega a corrente no seuO gerador pega a corrente no seu
potencial mais baixo (-) e passa para opotencial mais baixo (-) e passa para o
potencial mais alto (+).potencial mais alto (+).

4. FORÇA ELETROMOTRIZ (E)
Representa a energia fornecida a
cada unidade de carga da
corrente elétrica, ou seja, é a
ddp total do gerador.
E: F.E.M
U: ddp útil
r: resistência interna do
gerador
R: resistência externa do
elemento que recebera
energia elétrica do gerador.

5. EQUAÇÃO DO
GERADOR
U = E – r.i
Gerador ideal
r = 0r = 0
U = E
U = E - Udissipado

6. GRÁFICO DO GERADOR
U
i
E
icc
iicccc é a corrente de curto-é a corrente de curto-
circuito (máxima).circuito (máxima).
r
E
icc =
U = E – r.i

7. A B
Série
r1E1 r2E2 r3E3
A B
reqEeq
Gerador Equivalente
Eeq = E1 + E2 + E3
req = r1 + r2 + r3

8. Paralelo
rE
rE
rE
A B
Eeq = E
A B
reqEeq
Gerador Equivalente
n
r
req =
no
de
geradores

9. RECEPTOR ELÉTRICO
Dispositivo que transforma energia elétrica
em outra modalidade de energia, desde que
não seja totalmente em energia térmica.

10. SÍMBOLO DO RECEPTOR
E’
i
+
-r
O receptor pega a corrente no seuO receptor pega a corrente no seu
potencial mais alto (+) e passa para opotencial mais alto (+) e passa para o
potencial mais baixo (-).potencial mais baixo (-).

11. FORÇA CONTRA-ELETROMOTRIZ (E’)
Representa a energia elétrica que
cada unidade de carga da corrente
fornece ao receptor, ou seja, é a ddp
ÚTIL do RECEPTOR.
U
E´

12. EQUAÇÃO DO RECEPTOR
U = E’ + r.i
E´ = U – r.i
Obs: A ddp U no gerador representa a ddp útil,
enquanto que no receptor ele é a ddp total.

13. GRÁFICO DO RECEPTOR
U
i
E’

14. LEIS DE KIRCHHOFF
Lei dos nós
∑ ∑= saemchegam ii
i2
i1
i3
i4

15. ∑ =++ 0)( resistoresreceptoresgeradores UUU
E 1 E 2
E 3
E 4
R 1
R 2
R 3
i
LEI DAS MALHAS
EE11, E, E44 são geradores.são geradores.
EE22, E, E33 são receptores.são receptores.
R são resistoresR são resistores
Adotamos para E: (-) nos geradores e (+) nos receptores

16. LEI DE OHM GENERALIZADA
E 1 E 2
E 3
E 4
R 1
R 2
R 3
i
A
B
∑ ++= )( resistoresreceptoresgeradoresAB UUUU

17. Na figura a seguir observa-se um circuito elétrico com
dois geradores (E1 e E2) e alguns resistores.
Utilizando a 1ª lei de Kircchoff ou lei dos nós, pode-se
afirmar que
a) i1 = i2 – i3
b) i2 + i4 = i5
c) i4 + i7 = i6
d) i2 + i3 = i1
e) i1 + i4 + i6 = 0.
Resp.:D

18. Três pilhas de f.e.m E=1,5V e resistência interna r=1,0Ω são
ligadas como na figura a seguir.
A corrente que circula pelas pilhas é de
a) 0,50A, no sentido horário.
b) 0,50A, no sentido anti-horário.
c) 1,5A, no sentido horário.
d) 2,0A, no sentido anti-horário.
e) 2,0A, no sentido horário.
Resp.:A

19. (uem) Considere o circuito eletrico abaixo, em que e1 = 30
V; e2 = 120 V; R1 = 30 Ω ; R2 = 60 Ω e R3 = 30 Ω.
Assinale a alternativa que corresponde a corrente eletrica
que passa por R3. (Considere ”1 e ”2 geradores ideais.)

20. O valor da intensidade de correntes (em A) no circuito a seguir é:
a) 1,50
b) 0,62
c) 1,03
d) 0,50
e) 0,30

21. SISTEMAS DE MALHAS
-Use a lei dos nós em um dos nós.
-Para cada malha, escolha um sentido para circulação da
corrente(caso exista dois sentidos).
-Use a lei das malhas para cada uma das malhas, resultando
em um sistema de equações.

22. i1
R1
R
2
R3
ε1
ε2
i3
i2
a b c
d
(Uem) Relativamente ao circuito elétrico representado na figura
a seguir, assuma que R1 = 10,0 Ω, R2 = 15,0 Ω, R3 = 5,0 Ω, ”E1
= 240,0 mV e E2 = 100,0 mV. Assinale o que for correto.

23. 01) No nó b, i2 = i1 – i3.
V - aplicando a lei dos nós.
Malha 1:
0=++ resrecger UUU
0.15.1024,0 21 =++− ii
24,015.25 31 =− ii
i1
R1
R2
R3
ε1
ε2
i3
i2
a b c
d
I II

24. Malha 2:
0.5.151,0 32 =+− ii
1,02015 31 =− ii
i1
R1
R2
R3
ε1
ε2
i3
i2
a b c
d
I II

25. 24,015.25 31 =− ii
1,02015 31 =− ii
i1=0,012 A
i2=0,008 A
i3= 0,004 A

26. 02) F - A corrente elétrica i2 que atravessa o resistor R2 é menor
do que a corrente i3 que atravessa o resistor R3.
04) V - O valor da potência elétrica fornecida ao circuito
pelo dispositivo de força-eletromotriz ”E1” é 2,88 mW.
11.iP ε=
08) F - Aplicando a Lei das Malhas (de Kirchhoff) à malha
externa 'abcda' do circuito, obtém-se a equação
E1+E2=R1.i1+R3.i3
16)F - A diferença de potencial elétrico Vb - Vd entre
os pontos b e d do circuito vale 150,0 mV.
22.2
iRUR =

27. 32) F - A potência dissipada no resistor R2 vale 1,50 mW.
2
22.2
iRPR =
64) V - O valor da potência elétrica dissipada pelo
dispositivo de força-contra-eletromotriz E2‚ é 0,40 mW.
22.iP ε=