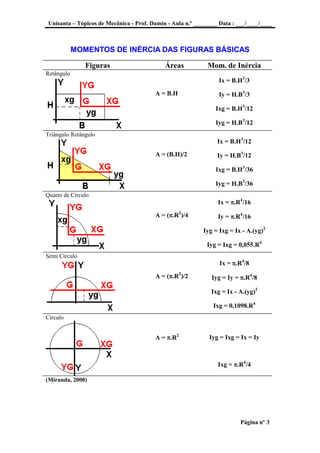
O documento discute o momento de inércia de figuras planas. Define o momento de inércia como a soma dos momentos de segunda ordem de cada área infinitesimal da figura em relação a um eixo de referência. Apresenta fórmulas para calcular o momento de inércia de formas básicas como retângulos e círculos. Também introduz o Teorema de Steiner, que relaciona o momento de inércia em relação a um eixo de referência com o momento de inércia em relação ao eixo baricênt

1. Unisanta – Tópicos de Mecânica - Prof. Damin - Aula n.º ________ Data : ___/____/____
Página nº 1
Momento De Inércia De Uma Figura Plana
Definição: (Murat, S.D.)
Seja uma figura plana qualquer, posicionada em
relação a um par de eixos de referência. Define-
se:
dIx = y2
.da
dIy = x2
.da
Considerado momento de 2ª ordem, momento de
1ª ordem é o estático.
Aplicando-se as definições acima para todos os
da, e somando-os temos:
Ix = (A) y2
.da
Iy = (A) x2
.da
Pela análise dimensional dessas definições, teremos como unidades para o MOMENTO
DE INÉRCIA: m4
, cm4
, pol4
, etc.
Será adotada a unidade de m4
(metro a quarta).
Exercício Aplicativo para Cálculo do Momento Inércia:
Aplicar as definições acima para o Retângulo, posicionado em relação aos eixos, nas seguintes
situações:
Situação 1: Situação 2:
Cálculo:
Ix = (A) y2
.da sendo da=B.dy
Ix = (A) y2
.B.dy
Ix = B.(y3
/3)0H
Ix = (B.H3
)/3
Logo: Iy = (H.B3
)/3
Cálculo:

2. Unisanta – Tópicos de Mecânica - Prof. Damin - Aula n.º ________ Data : ___/____/____
Página nº 2
Considerações:
 Apesar de ser usado um par de eixos de referência (X e Y), o cálculo do Momento de Inércia
(Ieixo) é feito em relação a cada um deles separadamente, Podendo os eixos serem quaisquer
ou baricêntricos.
 De acordo com a distribuição da área da figura plana ao redor do eixo de referência, o
Momento de Inércia sempre resultará um número positivo.
 Se, o eixo de referência for um eixo de simetria, o eixo será baricêntrico. O inverso não é
verdadeiro.
 À medida que o eixo de referência se afasta do baricentro da figura plana, o resultado do
momento de inércia, em relação ao eixo de referência, aumenta.
Nomenclatura Utilizada:
Baricentro = G
Coordenadas de baricentro = xg e yg
Eixos de Referência = X e Y
Eixos baricêntricos = XG e YG
Momentos de Inércia para os eixos de referência = IX e IY
Momentos de Inércia para os eixos baricêntricos = IXG e IYG
Área da figura plana = A
Área infinitesimal = dA

3. Unisanta – Tópicos de Mecânica - Prof. Damin - Aula n.º ________ Data : ___/____/____
Página nº 3
MOMENTOS DE INÉRCIA DAS FIGURAS BÁSICAS
Figuras Áreas Mom. de Inércia
Retângulo
A = B.H
Ix = B.H3
/3
Iy = H.B3
/3
Ixg = B.H3
/12
Iyg = H.B3
/12
Triângulo Retângulo
A = (B.H)/2
Ix = B.H3
/12
Iy = H.B3
/12
Ixg = B.H3
/36
Iyg = H.B3
/36
Quarto de Círculo
A = (.R2
)/4
Ix = .R4
/16
Iy = .R4
/16
Iyg = Ixg = Ix - A.(yg)2
Iyg = Ixg = 0,055.R4
Semi Círculo
A = (.R2
)/2
Ix = .R4
/8
Iyg = Iy = .R4
/8
Ixg = Ix - A.(yg)2
Ixg = 0,1098.R4
Círculo
A = .R2
Iyg = Ixg = Ix = Iy
Ixg = .R4
/4
(Miranda, 2000)

4. Unisanta – Tópicos de Mecânica - Prof. Damin - Aula n.º ________ Data : ___/____/____
Página nº 4
TEOREMA DE STEINER
Teorema da Translação de Eixos
Definição:(Murat, S.D.)
O momento de Inércia de uma Figura plana, em relação a um eixo qualquer, é igual à
soma do momento de inércia da figura, em relação ao seu eixo baricêntrico paralelo ao
eixo qualquer, com o produto da distância ao quadrado entre os eixos, pela área da
figura.
I = I + d2
.Afig
Demonstração:
Utilizaremos os resultados obtidos no cálculo do momento de inércia do retângulo para
demonstrarmos este teorema:
Ou seja: IX - IXG = ?
Solução:
Ix = B.H3
/3
Ixg = B.H3
/12
Logo: [B.H3
/3] - [B.H3
/12] = [(4B.H3
) - (B.H3
)]/12
Desta Forma:
IX - IXG = B.H3
/4
Reparar que, o valor encontrado pode ser decomposto em:
B.H3
/4 = (H2
/4).( B.H)
B.H3
/4 = (yg)2
.( A)
Analogamente:
IX = IXG + (yg)2
.( A)
IY = IYG + (xg)2
.( A)

5. Unisanta – Tópicos de Mecânica - Prof. Damin - Aula n.º ________ Data : ___/____/____
Página nº 5
Determinar os Momentos de Inércia das seguintes Figuras Compostas:
(P1 - 1º semestre, 1998)
Exemplo 15: Resposta: IX ; IY ; IXG ; IYG
Exemplo 16: Resposta: IX ; IY ; IXG ; IYG
9 cm3 cm
2 cm
7 cm
3 cm

6. Unisanta – Tópicos de Mecânica - Prof. Damin - Aula n.º ________ Data : ___/____/____
Página nº 6
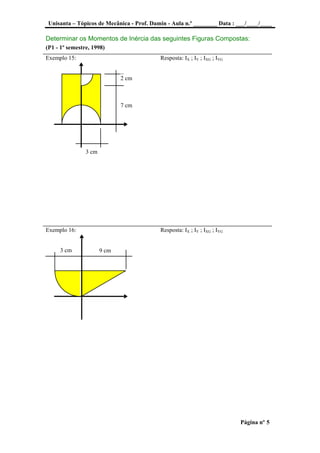
Determinar os Momentos de Inércia das seguintes Figuras Compostas:
Exemplo 17:
Da aula anterior temos:
Área da Figura 1 (4º círculo) = 28,27 cm2
Área da Figura 2 (triângulo) = 13,5 cm2
.
Coordenada yg2 = 4 cm
Área da Figura 3 (triângulo) = 13,5 cm2
.
Coordenada yg3 = 2 cm
Coordenadas do Baricentro: G = (xg ; yg)
G = (0,16 ; 2,77) cm.
Área da Figura Total (AT)= 55,27 cm2
.
Resposta:
Cálculo de IX:
IX = IX1 + [IXG2 + A2.(yg2)2
] + [IXG3 +
A3.(yg3)2
] =
IX = .(6)4
/16 + [9.(3)3
/36 + 13,5.(4)2
] +
[9.(3)3
/36 + 13,5.(2)2
] = 537,97 cm4
.
Cálculo de IXG (aplicando Steiner),
temos:
IXG = IX - AT.(yg)2
=
IXG = 537,97 - 55,27.(2,77)2
= 113,89 cm4
.
Cálculo de IY: (as figuras tocam o eixo Y)
IY = IY1 + IY2 + IY3 =
IY = .(6)4
/16 + 3.(9)3
/12 + 3.(9)3
/12 =
IY = 618, 96 cm4.
Cálculo de IYG (aplicando Steiner),
temos:
IYG = IY - AT.(xg)2
=
IYG = 618, 96 - 55,27.(0,16)2
=
IYG = 617, 54 cm4
.
Exemplo 18 Resposta:
3
2
1

7. Unisanta – Tópicos de Mecânica - Prof. Damin - Aula n.º ________ Data : ___/____/____
Página nº 7
Exercício 18:
Calcular, para a figura plana abaixo, o Baricentro e os Momentos de Inércia para os eixos de
referência (X eY), bem como, para os eixos baricêntricos. Posicionar o Ponto de Baricentro (G)
na figura, indicando suas coordenadas no desenho e a posição dos eixos baricêntricos.
Utilizar as unidades no Sistema Internacional.
Solução:
3 x 10-2
m
5 x 10-2
m
X
Y