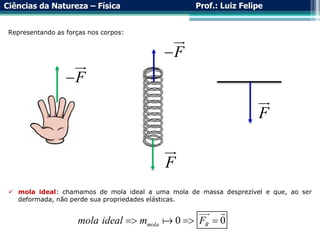
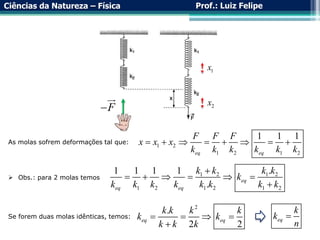
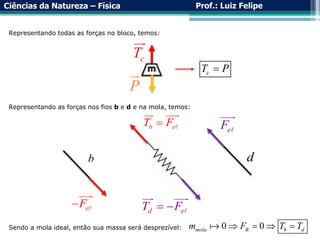
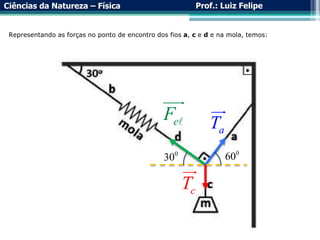
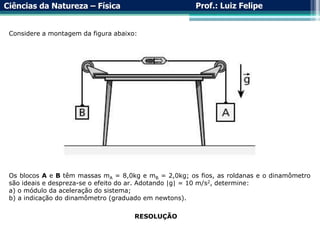
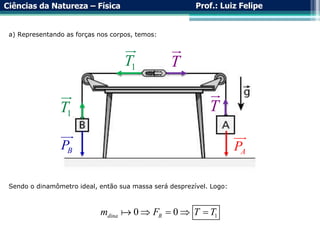
O documento aborda a força elástica e a Lei de Hooke, explicando a deformação de molas e suas aplicações em sistemas de molas em série e em paralelo. Examina a propriedade restauradora das molas e a relação entre forças aplicadas e deformações, além de discutir a utilização de dinamômetros para medir força. Exemplos práticos são incluídos para ilustrar a teoria.

1. Ciências da Natureza – Física Prof.: Luiz Felipe
Força elástica
 Lei de Hooke
Considere uma mola de comprimento inicial L0 e com uma das extremidades fixa.
Aplicando à outra extremidade uma força de módulo F de mesma direção da mola até seu
comprimento aumentar para L, teremos que a diferença L – L0 será a deformação x da mola.

2. Ciências da Natureza – Física Prof.: Luiz Felipe

3. Ciências da Natureza – Física Prof.: Luiz Felipe
Representando as forças nos corpos:
F
F
F

F

 mola ideal: chamamos de mola ideal a uma mola de massa desprezível e que, ao ser
deformada, não perde sua propriedades elásticas.
0 0
mola R
mola ideal m F
  

4. Ciências da Natureza – Física Prof.: Luiz Felipe
 Obs.: tanto no caso em que a mola é esticada quanto no caso em que é comprimida, ao
retirarmos a força que causou a deformação, a tendência da mola é voltar ao seu
comprimento inicial.
força restauradora
 Obs.: materiais que, quando deformados, não conseguem voltar à sua forma original,
possuem comportamento plástico. Já aqueles que retomam a sua forma original depois que
a causa da deformação desaparece possuem comportamento elástico.
A experiência mostra que, desde que x não seja muito grande em comparação com L0, a
intensidade da força elástica será diretamente proporcional à deformação:
F kx

k é a constante elástica da mola (sua unidade SI é N/m)
 Obs.: a constante elástica representa a dureza da mola

5. Ciências da Natureza – Física Prof.: Luiz Felipe
Robert Hooke
Bruce Banner

6. Ciências da Natureza – Física Prof.: Luiz Felipe
Graficamente temos:
 Associação de molas
 Associação em série
Considere duas molas ideais, de constantes elásticas k1 e k2, associadas em série. Se
aplicarmos ao conjunto uma força, sua deformação será x. Chamamos de mola equivalente à
associação uma única mola de constante elástica k que, sob ação da mesma força, terá a
mesma deformação.
e
F
x
a
ka

N N
ka
tg tg k
a
 
  
equação característica
e
F kx


7. Ciências da Natureza – Física Prof.: Luiz Felipe
As molas sofrem deformações tal que:
 Obs.: para 2 molas temos
1
x
2
x
1 2
1 2 1 2
1 1 1
eq eq
F F F
x x x
k k k k k k
       
F

1 2 1 2
1 2 1 2 1 2
.
1 1 1 1
.
eq
eq eq
k k k k
k
k k k k k k k k

     

Se forem duas molas idênticas, temos:
2
.
2 2
eq eq
k k k k
k k
k k k
   

eq
k
k
n


8. Ciências da Natureza – Física Prof.: Luiz Felipe
Cada uma das molas receberá uma força de intensidade F/2. Pela Lei de Hooke temos:
1 1 1 1
2 2 2
2
F
k x F k x kx k x k k
      
Para “n” molas temos:
1
k nk
 número de molas
 Associação em paralelo
Considere duas molas idênticas de constante elástica k1 associadas em paralelo. As
molas estão presas a um mesmo suporte S e a uma barra de massa desprezível, no centro da
qual é aplicada uma força. O sistema então sofrerá uma deformação x.
Seja k a constante elástica da mola equivalente. Sob ação da mesma força, ela
sofrerá a mesma deformação x.
1
2
F

9. Ciências da Natureza – Física Prof.: Luiz Felipe
(UNICEUB-2019/2) Para embalar areia em sacos de 20kg, um fluxo constante de areia é
despejado em um recipiente de pesagem apoiado em uma mola, que obedece à lei de Hooke.
Quando o comprimento inicial da mola é reduzido em 3cm, um sensor interrompe o
fornecimento da areia e deposita o conteúdo do recipiente em um saco plástico. Para encher
sacos com 50kg de areia, o sensor deve ser regulado para interromper o fornecimento de
areia no momento em que a mola tenha seu comprimento inicial reduzido em
a) 5,0cm. b) 7,5cm. c) 4,5cm. d) 15,0cm. e) 6,0cm.
RESOLUÇÃO
Para a situação inicial (sacos de 20kg), temos:
P
e
F 200
.3 20.10
3
e
N
F P kx mg k k
cm
      
Para o saco de 50kg, temos
e
F P kx mg
  
200
50.10 7,5
3
x x cm
  
B

10. Ciências da Natureza – Física Prof.: Luiz Felipe
(UFPR-2017) Uma mola de massa desprezível foi presa a uma estrutura por meio da corda
“b”. Um corpo de massa m igual a 2000g está suspenso por meio das cordas “a”, “c” e “d”,
de acordo com a figura, a qual representa a configuração do sistema após ser atingido o
equilíbrio. Considerando que a constante elástica da mola é 20 N/cm e a aceleração
gravitacional é 10 m/s2, assinale a alternativa que apresenta a deformação que a mola sofreu
por ação das forças que sobre ela atuaram, em relação à situação em que nenhuma força
estivesse atuando sobre ela. Considere ainda que as massas de todas as cordas e da mola são
irrelevantes.
a) 0,5cm. b) 1,2cm. c) 2,5cm. d) 3,5cm. e) 5,2cm.
RESOLUÇÃO

11. Ciências da Natureza – Física Prof.: Luiz Felipe
Representando todas as forças no bloco, temos:
Sendo a mola ideal, então sua massa será desprezível: 0 0
mola R b d
m F T T
   
b
e
F
d e
T F
 
d
b e
T F

e
F

c
T
P
c
T P

Representando as forças nos fios b e d e na mola, temos:

12. Ciências da Natureza – Física Prof.: Luiz Felipe
e
F
a
T
c
T
Representando as forças no ponto de encontro dos fios a, c e d e na mola, temos:
0
30
0
60

13. Ciências da Natureza – Física Prof.: Luiz Felipe
Decompondo a força elástica e a tração no fio a, temos:
EIXO X
0 0
.cos30 .cos60 3
X X
e a e a a e
F T F T T F
    
EIXO Y
0 0
. 30 . 60
Y Y
e a C e a
F T T F sen T sen P
    
1 3
. 3 . 2 2.20. 2.10
2 2
kx kx mg kx mg x
     
Logo: 0,5
x cm

A

14. Ciências da Natureza – Física Prof.: Luiz Felipe
 Dinamômetro
Considere uma mola com uma de suas extremidades fixas. Aplicando à outra extremidade uma
força, a mola deforma-se até que seja estabelecido o equilíbrio. Se adaptarmos uma escala
graduada a essa mola, teremos um instrumento para medir intensidades de força. Esse
instrumento é o dinamômetro.
A força resultante no dinamômetro, suposto de massa desprezível (dinamômetro ideal), é nula.
Suas extremidades são puxadas por forças opostas.
o dinamômetro indica a intensidade da força aplicada em uma das suas extremidades

15. Ciências da Natureza – Física Prof.: Luiz Felipe

16. Ciências da Natureza – Física Prof.: Luiz Felipe
Considere a montagem da figura abaixo:
Os blocos A e B têm massas mA = 8,0kg e mB = 2,0kg; os fios, as roldanas e o dinamômetro
são ideais e despreza-se o efeito do ar. Adotando |g| = 10 m/s2, determine:
a) o módulo da aceleração do sistema;
b) a indicação do dinamômetro (graduado em newtons).
RESOLUÇÃO

17. Ciências da Natureza – Física Prof.: Luiz Felipe
a) Representando as forças nos corpos, temos:
A
P
B
P
1
T
1
T T
T
Sendo o dinamômetro ideal, então sua massa será desprezível. Logo:
1
0 0
dina R
m F T T
   

18. Ciências da Natureza – Física Prof.: Luiz Felipe
2
80 20 10 6
A A
B B
P T m a
T P m a
m
a a
s
 


 

   
Aplicando a 2ª Lei de Newton para os blocos, temos:
b) O dinamômetro marca a força que atua em uma de suas extremidades, logo:
20 2.6 32
B B
T P m a T T N
      

19. Ciências da Natureza – Física Prof.: Luiz Felipe
(FUVEST) Um dinamômetro acusa 12 N ao sustentar uma corrente formada por 60 elos
idênticos e independentes. Apoiando-se completamente 15 elos sobre uma mesa horizontal:
a) qual será o valor da massa da parte suspensa pela corrente?
b) qual será o valor da força exercida pela superfície sobre os 15 elos?
(Adote g = 10 m/s2.)
RESOLUÇÃO
b) Representando as forças que atuam na corrente, temos:
ap
P
sus
P
N
F
at
f
12 .10 1,2
corrente corr corr corr
P m g m m kg
    
60 1,2
45 0,9
sus sus
elos kg
elos m m kg
   
     
Para a força normal, temos:
 
N ap N ap N corr sus
F P F m g F m m g
     
 
1,2 0,9 .10 3,0
N N
F F N
   