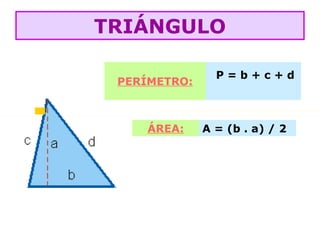
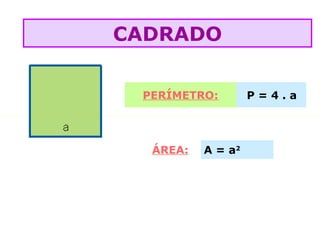
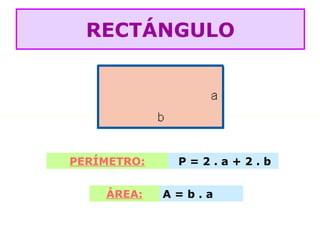
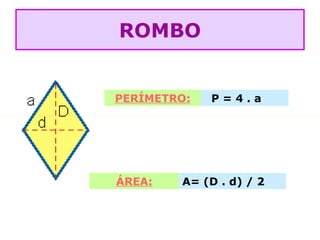
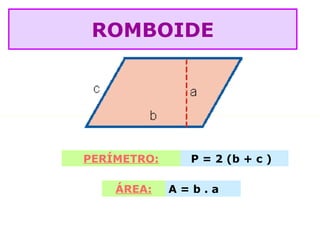
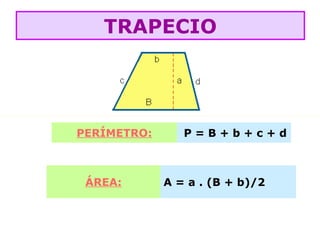
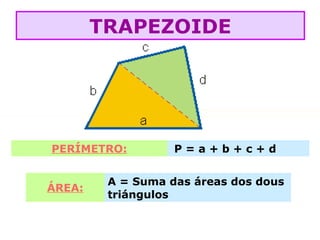
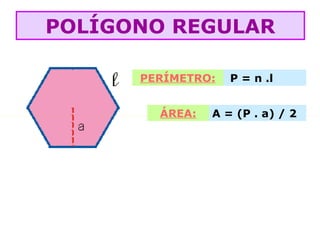
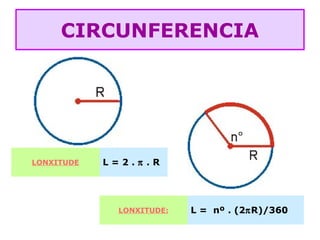
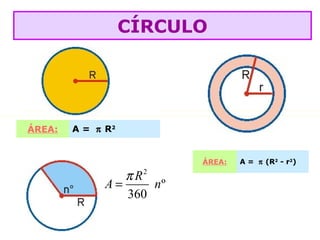
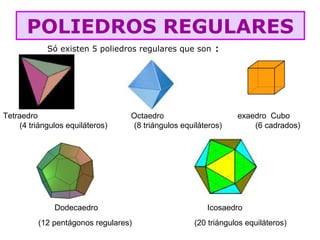
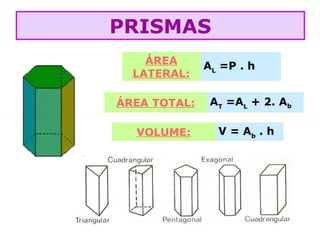
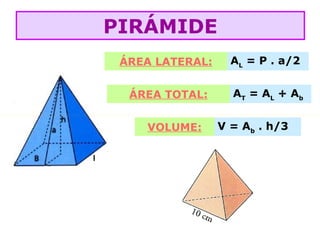
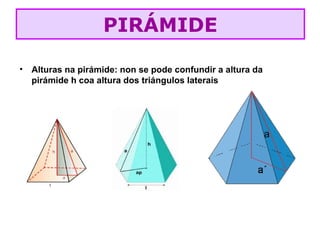
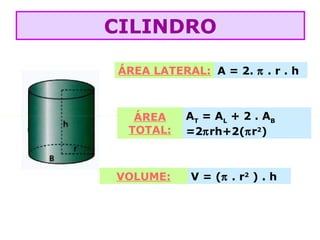
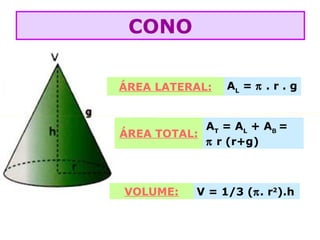
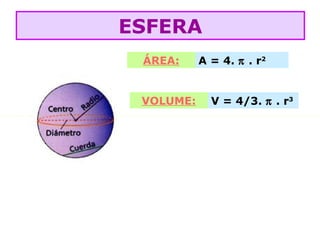
O documento lista as fórmulas para calcular perímetros e áreas de várias figuras geométricas planas e sólidas, incluindo triângulos, quadrados, retângulos, rombos, trapézios, círculos, esferas, pirâmides, prismas e cilindros. Também descreve os cinco poliedros regulares e fornece detalhes sobre vértices, arestas e faces em poliedros convexos.

1. XEOMETRÍA

2. PERÍMETRO:
P = b + c + d
ÁREA: A = (b . a) / 2
TRIÁNGULO

3. PERÍMETRO: P = 4 . a
ÁREA: A = a2
CADRADO

4. PERÍMETRO: P = 2 . a + 2 . b
ÁREA: A = b . a
RECTÁNGULO

5. PERÍMETRO: P = 4 . a
ÁREA: A= (D . d) / 2
ROMBO

6. PERÍMETRO: P = 2 (b + c )
ÁREA: A = b . a
ROMBOIDE

7. PERÍMETRO: P = B + b + c + d
ÁREA: A = a . (B + b)/2
TRAPECIO

8. PERÍMETRO: P = a + b + c + d
ÁREA:
A = Suma das áreas dos dous
triángulos
TRAPEZOIDE

9. PERÍMETRO: P = n .l
ÁREA: A = (P . a) / 2
POLÍGONO REGULAR

10. CIRCUNFERENCIA
LONXITUDE L = 2 . π . R
LONXITUDE: L = nº . (2πR)/360

11. ÁREA: A = π R2
2
º
360
R
A n
π
=
ÁREA: A = π (R2
- r2
)
CÍRCULO

12. Tetraedro Octaedro hexaedro Cubo
(4 triángulos equiláteros) (8 triángulos equiláteros) (6 cadrados)
Dodecaedro Icosaedro
(12 pentágonos regulares) (20 triángulos equiláteros)
POLIEDROS REGULARES
Só existen 5 poliedros regulares que son :

13. POLIEDROS
REGULARES

14. ÁREA
LATERAL:
AL
=P . h
ÁREA TOTAL: AT
=AL
+ 2. Ab
VOLUME: V = Ab
. h
PRISMAS

15. ÁREA LATERAL: AL
= P . a/2
ÁREA TOTAL: AT
= AL
+ Ab
VOLUME: V = Ab
. h/3
PIRÁMIDE

16. • Alturas na pirámide: non se pode confundir a altura da
pirámide h coa altura dos triángulos laterais a
PIRÁMIDE

17. ÁREA LATERAL: A = 2. π . r . h
ÁREA
TOTAL:
AT
= AL
+ 2 . AB
=2πrh+2(πr2
)
VOLUME: V = (π . r2
) . h
CILINDRO

18. ÁREA LATERAL: AL
= π . r . g
ÁREA TOTAL:
AT
= AL
+ AB
=
=π rg+ π r2
VOLUME: V = 1/3 (π. r2
).h
CONO

19. ÁREA: A = 4. π . r2
VOLUME: V = 4/3. π . r3
ESFERA

20. TRONCO
PIRÁMIDE
TRONCO
CONO

21. Nos poliedros convexos
Vértices+Caras=Arestas+2
Poliedro convexo Poliedro no convexo
FÓRMULA DE EULER

22. TETRAEDROS

23. ORTOEDRO
DODECAEDRO

24. CILINDROS

25. PRISMAS

26. PRISMAS OBLICUOS

27. PRISMA OCTOGONAL

28. PIRÁMIDES

29. CONOS
Catedral Maringá, Brasil.

30. ESFERAS

31. FIGURAS COMPOSTAS

32. FIGURAS COMPOSTAS