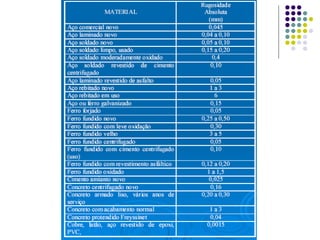
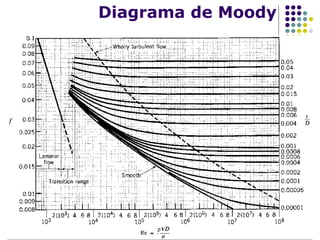
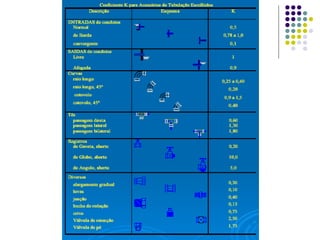
O documento discute perdas de carga em fluidos, que é a energia dissipada por um fluido ao passar por um conduto. Existem perdas distribuídas ao longo de trechos retos e perdas localizadas em junções, curvas e válvulas. A fórmula de Darcy-Weissbach pode ser usada para calcular perdas distribuídas usando o coeficiente de atrito, enquanto perdas localizadas são calculadas usando a energia cinética do fluido.

1. Mecânica dos Fluidos Equação de Bernoulli para fluidos reais

12. Diagrama de Moody