Transferir como PDF, PPTX
Carregado porRafael Jegundo
Aulas Cap 3
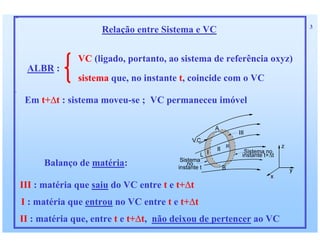
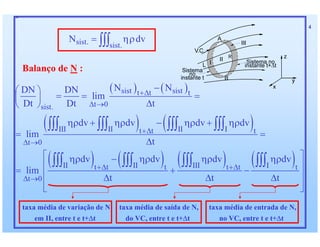
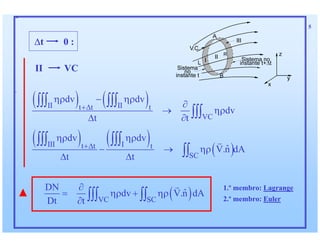
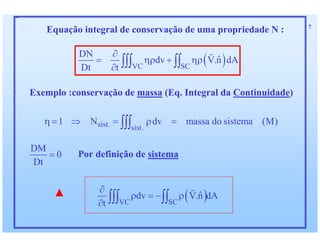
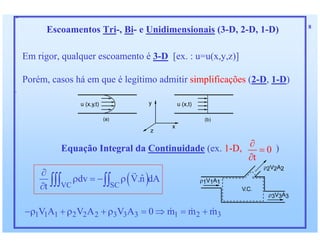
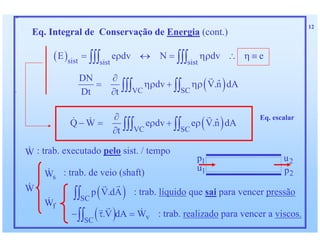
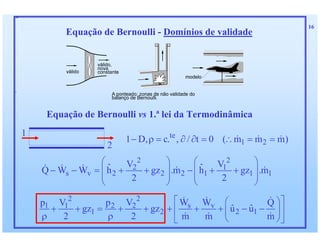
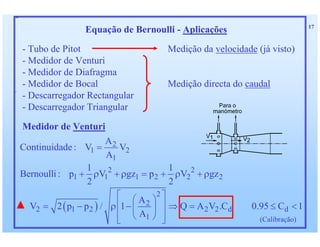
1) O documento discute as relações integras aplicadas a volumes de controle e como elas podem ser usadas para derivar equações de conservação para propriedades como massa, quantidade de movimento e energia. 2) Essas equações de conservação são derivadas igualando a taxa de variação da propriedade dentro do volume de controle com os fluxos líquidos através da superfície de controle. 3) Exemplos de equações de conservação derivadas incluem a equação da continuidade, equações de conservação de quantidade de movimento linear e angular,
