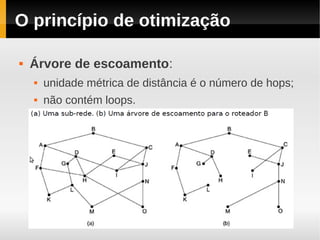
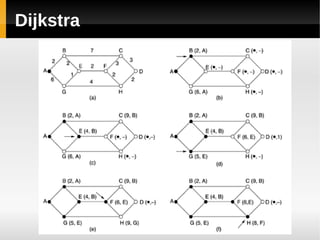
O documento discute princípios de otimização e algoritmos de roteamento, especificamente: (1) O princípio de otimização busca rotas ótimas sem levar em conta a topologia da rede, formando uma árvore de escoamento com o destino na raiz; (2) O algoritmo de roteamento pelo caminho mais curto cria um grafo da rede e escolhe a rota com menos hops entre pares de roteadores; (3) O algoritmo de Dijkstra, um exemplo de algoritmo de caminho mais curto, atribui

1. CENTRO FEDERAL DE EDUCAÇÃO TECNOLÓGICA DE MINAS GERAIS
ALGORITMOS DE ROTEAMENTO
Princípio de Otimização / Caminho mais curto
Anna Cláudia Almeida
Arthur Alcantara
Diogo Victor
Paula Peçanha
Renan Brum

2. O princípio de otimização
 É a possibilidade de criar uma descrição geral
das rotas ótimas sem levar em conta a
topologia ou o tráfego de rede.
 O conjunto de rotas ótimas de todas as origens
para um determinado destino forma uma árvore
com raiz no destino (árvore de escoamento).

3. O princípio de otimização
 Árvore de escoamento:
 unidade métrica de distância é o número de hops;
 não contém loops.

4. O princípio de otimização
 Problema: Enlaces e roteadores podem sair do ar
e voltar à atividade durante a operação.
 Cada roteador deve obter individualmente as
informações sobre a base do cálculo de sua árvore
de escoamento.
 O princípio da otimização e a árvore de
escoamento permitem que se faça um teste de
benchmark para detectar que outros algoritmos de
roteamento podem ser medidos.

5. Roteamento pelo caminho mais
curto
 Cria um grafo da sub-rede, com cada nó do grafo
representando um roteador e cada arco indicando
uma linha de comunicação (enlace).
 Para escolher uma rota entre um determinado par
de roteadores, o algoritmo encontra o caminho
mais curto:
 Caminho mais curto = número de hops;
 Caminho mais curto = distância física;
 Caminho mais curto = caminho mais rápido.

6. Roteamento pelo caminho mais
curto
 Alterando-se a função de ponderação (atribuição
de pesos), o algoritmo calcularia o caminho "mais
curto" medido de acordo com qualquer critério ou
com uma combinação de critérios.
Um dos exemplos
mais conhecidos de
algoritmo de
caminho mais curto
é o Algoritmo de
Dijkstra (1959).

7. Dijkstra
 Passo 1: Os caminhos não são conhecidos:
 Atribuir o valor infinito a todos os nós;
 Passo 2: À medida que os caminhos são
encontrados:
 Mudam-se os rótulos, refletindo os melhores
caminhos, porém ainda são provisórios;
 Se for o melhor caminho o rótulo se torna
permanenete.

8. Dijkstra