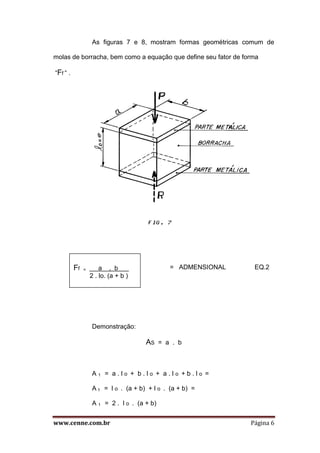
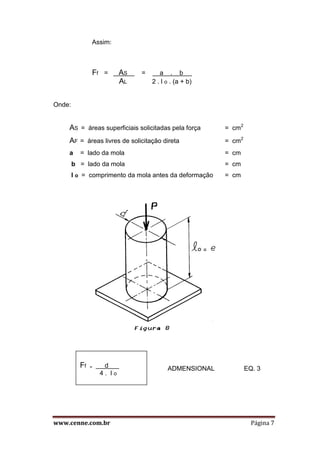
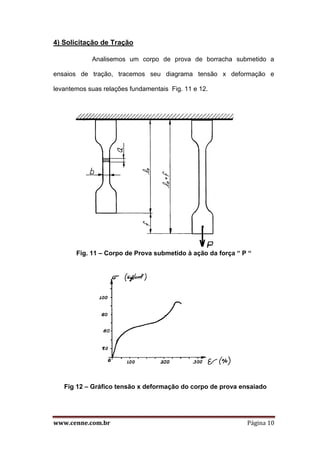
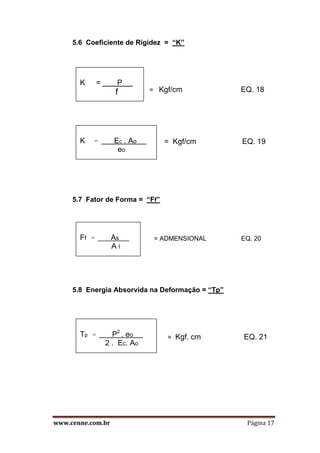
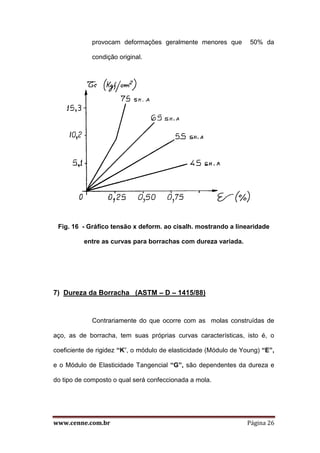
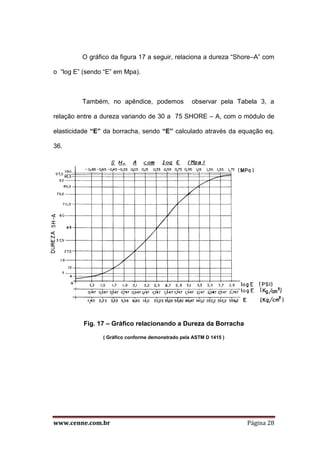
O documento discute o comportamento estático de molas e coxins de borracha. Apresenta as propriedades viscoelásticas da borracha e como afetam a deformação sob carga. Explica como o fator de forma influencia a rigidez e como ele pode ser alterado para atender diferentes aplicações. Também descreve as equações fundamentais para dimensionar molas sob tração e compressão estática.