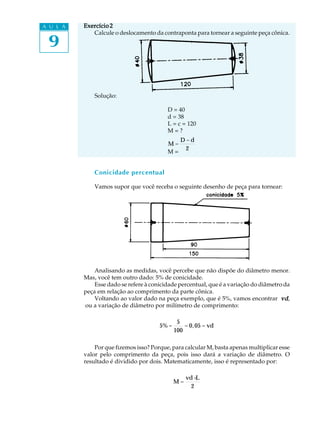
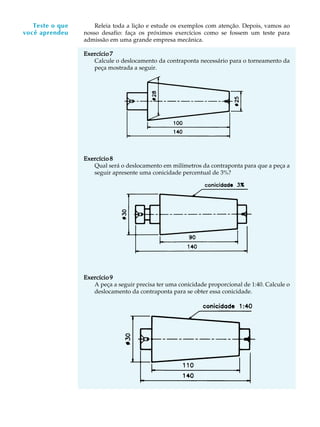
O documento descreve como calcular o deslocamento necessário da contraponta para tornear peças cônicas usando a técnica do desalinhamento da contraponta. Existem três métodos para calcular o deslocamento: 1) usando os diâmetros maior e menor e o comprimento da parte cônica, 2) usando a conicidade percentual, e 3) usando a conicidade proporcional. Vários exemplos ilustram como aplicar cada método.