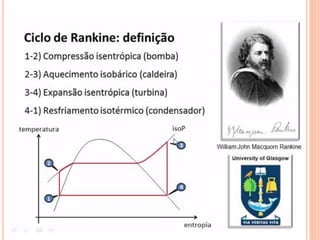
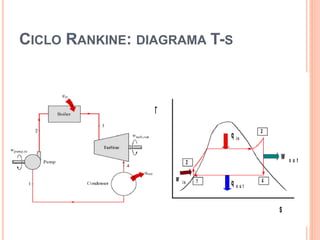
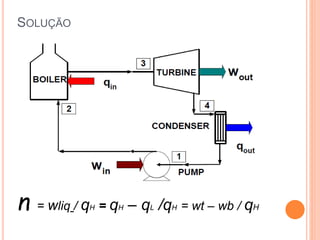
O documento discute ciclos termodinâmicos como o Ciclo de Carnot e o Ciclo de Rankine. O Ciclo de Rankine converte calor em trabalho usando vapor de água e é usado em 90% da geração de energia elétrica no mundo. O documento fornece um exemplo de como calcular o rendimento de um ciclo de Rankine.

1. CICLOS TERMODINÂMICOS
André Mario
Carlos Alberto
Julia Medina
Viviane Basílio
Ciclo Rankine

2. CICLOS DE POTÊNCIA A VAPOR
 Os ciclos a vapor para geração de potência nada
mais é do que a conversão de calor em Trabalho.

3. CICLO CARNOT
 Isso tudo aconteceu por volta de 1850 quando
surgiu a preocupação com a maior eficiência de
conversão.
 Nicolas Sadi Carnot criou o ciclo que leva seu
nome (Ciclo de Carnot).
 Ciclo Carnot x Ciclo Rankine

4. CICLO RANKINE
 Ciclo termodinâmico reversível que
converte calor em trabalho.
 O calor é suprido via externa para um laço
fechado, onde é usual usar água. Este ciclo
gera cerca de 90% de toda a energia
elétrica produzida no mundo, incluindo
virtualmente toda a energia
solar,biomassa,carvão e nuclear nas usinas
elétricas.
 Foi descoberto por William John Rankine,
um escocês e professor da Universidade de
Glasgow.

6. CICLO RANKINE: DIAGRAMA T-S

7. EXEMPLO
 Determine o rendimento de um ciclo de Rankine que
utiliza água como fluído de trabalho e no qual a
pressão no condensador é igual a 10 KPa.A pressão
na caldeira é de 2 Mpa. O vapor deixa a caldeira como
vapor saturado.

8. SOLUÇÃO
 Consideraremos, sucessivamente, uma superfície
de controle que envolve a bomba,caldeira,turbina e
condensador,assim como que o processo ocorre
em regime permanente.
 Em cada caso, o modelo termodinâmico adotado é
aquele associado às tabelas de vapor d'água e
consideraremos que o processo ocorre em regime
permanente, ou seja com variações de energias
cinética e potencial desprezíveis.

9. SOLUÇÃO
n = wliq / qH = qH – qL /qH = wt – wb / qH

10.  Consideremos inicialmente a bomba:
o Entrada: p1 conhecida, líquido saturado; estado
determinado.
o Saída: p2 conhecida.
Trabalho na bomba:
wb = v(p2-p1)
wb = 0,00101(2000-10)
wb = 2 KJ/kg
Entalpia na bomba:
h2 = h1 + wb
h2 = 191,8 + 2
h2 = 193,8
SOLUÇÃO

11.  Consideremos agora a caldeira:
o Entrada: p2, h2 conhecidas; estado determinado .
o Saída: p3 conhecida, vapor saturado; estado
determinado .
qH = h3-h2
qH = 2799,5 - 193,8
qH = 2605,7 kJ/kg
SOLUÇÃO

12.  Consideremos agora a turbina:
o Entrada: Estado 3 conhecido.
o Saída: p4 conhecida
o Lembrando que a 1ª lei : Wt = h3 – h4 ;
e a 2ª lei: s3 =s4
o Logo podemos determinar o título no estado 4 a partir da
entropia neste estado,assim:
s3 = s4 = 6,3409 = 0,6493 + x4 7,5009 => ,
x4 = 0.7588
h4 = 191,8 + 0,7588(2392,8) = 2007,5 kJ/kg
wt = 2799,5 - 2007,5 = 792,0 kJ/kg
SOLUÇÃO

13.  Finalmente, consideremos o condensador:
o Entrada: Estado 4, conhecido. Estado de
saída: Estado l, conhecido.
o Equação da energia:
qL = h4 – h1
qL = 2007,5 - 191,8
qL = 1815,7 kJ/kg
SOLUÇÃO

14. SOLUÇÃO
Podemos agora calcular o rendimento térmico :
o n = wliq / qH = qH – qL /qH = wt – wb / qH
o n = 792,0 – 2,0 / 2605,7
o n = 30,3 %
o Logo o rendimento térmico é 30,3%.