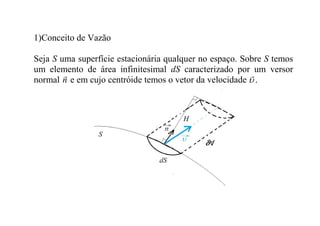
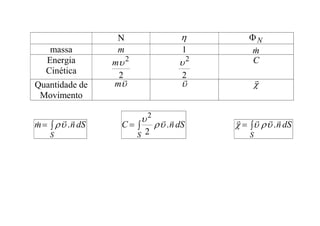
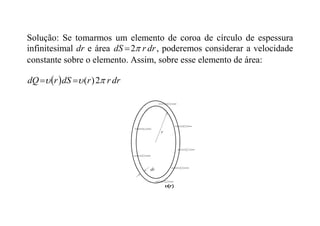
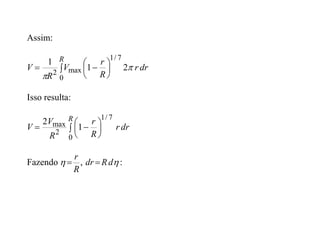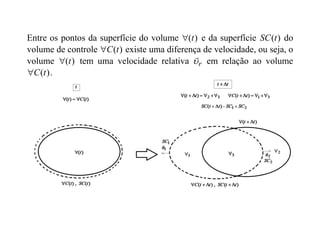
1) O documento discute conceitos de vazão, fluxo de massa, energia cinética e quantidade de movimento através de superfícies. É apresentado o Teorema do Transporte de Reynolds, que relaciona a variação temporal de propriedades de fluidos em movimento. 2) O Teorema expressa que a taxa de variação de uma propriedade em um volume de controle é igual à taxa de acréscimo da propriedade devido ao fluxo através da superfície de controle, mais a taxa de variação dentro do volume de controle.

1. Aula 2
Vazão, Teorema do transporte de Reynolds e
Equação da Continuidade.

2. 1)Conceito de Vazão
Seja S uma superfície estacionária qualquer no espaço. Sobre S temos
um elemento de área infinitesimal dS caracterizado por um versor
normal n

e em cujo centróide temos o vetor da velocidade 

.

3. Ao longo de um intervalo t
 um volume de fluido 
 passa através do
elemento superficial dS. O volume 
 é igual à área de sua base
multiplicada por sua altura. Assim:
dS
H



A altura H é igual à projeção na direção normal ao elemento de área dS
do produto entre o vetor da velocidade e o intervalo de tempo t
 . Assim:
t
n
H 



.

Logo, o volume 
 é dado por:
dS
t
n 




.



4. O volume de fluido por unidade de tempo que instantaneamente
atravessa o elemento superficial dS é dado por:
dS
n
t
dQ


.






Chamamos dQ de vazão volumétrica, fluxo de volume ou simplesmente
vazão. dQ é a vazão volumétrica através de dS. A vazão volumétrica
total através da superfície S será:


S
dS
n
Q


.

Dimensionalmente,   1
3 
 T
L
Q e sua unidade SI é m3
/s.

5. A velocidade média V sobre uma superfície S é dada pela divisão entre a
vazão Q e a área superficial S. Assim:



S
dS
n
S
S
Q
V


.
1

Assim como temos uma vazão volumétrica que representa a quantidade
de volume de fluido por unidade de tempo que atravessa
instantaneamente a superfície S, podemos falar em vazão em massa
quando queremos saber a quantidade de massa de fluido por unidade de
tempo que atravessa instantaneamente a superfície S. O volume 
 tem
uma massa dada por 
 

m , onde  é a massa específica.

6. Assim, a vazão em massa através de dS é dada por:
dS
n
t
m
m
d


 .






E a vazão em massa ou fluxo de massa através da superfície S é dada
por:


S
dS
n
m


 .


Dimensionalmente,   1

 T
M
m
 e sua unidade SI é kg/s.

7. Assim como temos um fluxo de massa através de uma superfície,
podemos ter também fluxos de Energia Cinética e Quantidade de
movimento.
O fluxo de Energia Cinética C através da superfície S é dado por:


S
dS
n
C


.
2
2



Em termos dimensionais,   3
2 
 T
ML
C e sua unidade SI é J/s ou W.

8. O fluxo de Quantidade de Movimento 

é dado por:


S
dS
n




.




Em termos dimensionais,   2

MLT
 e sua unidade SI é N.

9. Generalizando, o fluxo  de uma grandeza física N qualquer, inerente a
uma certa quantidade de massa de fluido (propriedade extensiva, ou
seja, depende da extensão da massa da amostra) pode ser representado
por:
dS
n
S
N


.






Onde  é a grandeza N por unidade de massa do fluido (propriedade
intensiva, ou seja, não depende da massa da amostra).

10. N  N

massa m 1 m

Energia
Cinética 2
2

m
2
2
 C
Quantidade de
Movimento


m 





S
dS
n
m


 .

 

S
dS
n
C


.
2
2





S
dS
n




.





11. Exemplo: Em condutos industriais de seção circular, o perfil de
velocidades é dado por:
 
7
/
1
max 1 







R
r
V
r

Onde Vmax é a velocidade na linha de centro, r é uma coordenada radial e
R é o raio do conduto. Obtenha uma expressão para a velocidade média
V.

12. Solução: Se tomarmos um elemento de coroa de círculo de espessura
infinitesimal dr e área dr
r
dS 
2
 , poderemos considerar a velocidade
constante sobre o elemento. Assim, sobre esse elemento de área:
  dr
r
r
dS
r
dQ 

 2
)
(



13. A vazão Q será:
  



R
S
dr
r
r
dS
r
Q
0
2
)
( 


E a velocidade média será:
  



R
S
dr
r
r
R
dS
r
S
V
0
2
2
)
(
1
1





14. Assim:
 







R
dr
r
R
r
V
R
V
0
7
/
1
max
2
2
1
1


Isso resulta:
 







R
dr
r
R
r
R
V
V
0
7
/
1
2
max 1
2
Fazendo
R
r

 , 
d
R
dr  :

15.  
 

1
0
7
/
1
2
max 1
2


 Rd
R
R
V
V
Isso resulta:
 
 

1
0
7
/
1
max 1
2 

 d
V
V
Fazendo     








 7
/
8
7
/
1
1
8
7
1 
 
d
d :

16.  
   










 
























 








1
0
7
/
8
1
0
7
/
8
max
1
0
7
/
8
max
1
8
7
1
8
7
2
1
8
7
2










d
d
d
V
d
d
d
V
V
Isso resulta:
 






 







1
0
7
/
8
max 1
8
7
2 
 d
V
V
Integrando:

17.  
1
0
7
/
15
max 1
15
7
8
7
2 













 
V
V
Isso resulta:















120
49
0
2 max
V
V
Logo:
max
60
49
V
V 

18. 2) Teorema do Transporte de Reynolds
Seja uma grandeza extensiva N(t) qualquer relacionada com uma certa
quantidade de massa m de um volume de fluido móvel e deformável
)
(t
 . Podemos dizer que N é dado por:
 

 )
(
)
(
t
d
t
N 

Suponha agora que, no instante t, o volume de fluido )
(t
 ocupa uma
posição no espaço coincidente com um volume arbitrário )
(t
C
 ,
também móvel e deformável. O contorno de )
(t
C
 é chamado de
Superfície de controle )
(t
SC .

19. Entre os pontos da superfície do volume )
(t
 e da superfície )
(t
SC do
volume de controle )
(t
C
 existe uma diferença de velocidade, ou seja, o
volume )
(t
 tem uma velocidade relativa r


em relação ao volume
)
(t
C
 .

20. Devido a essa velocidade relativa entre os dois volumes, em t
t 
 eles
não serão mais coincidentes.
Suponha agora que queremos estudar a variação temporal da grandeza N
da massa móvel de fluido. Assim:
t
t
N
t
t
N
dt
dN
t 






)
(
)
(
lim
0
Isso pode ser escrito como:
t
d
d
dt
dN t
t
t
t 
 

 







)
(
)
(
0
lim




21. Isso resulta:
t
d
d
dt
dN t
t 
 

 







)
(
0
3
2
lim



Vamos agora somar e subtrair na expressão acima o termo
t
d

 
1


:











 


 


 

 








 t
d
t
d
t
d
d
dt
dN t
t
1
2
3
1 )
(
0
lim







22. Lembrando que )
(
3
1 t
t
C 





 e :
)
(
)
( t
C
t 













 


 


 

 








 t
d
t
d
t
d
d
dt
dN t
C
t
t
C
t
1
2
)
(
)
(
0
lim






O primeiro termo representa a variação temporal da grandeza C
N não
mais da massa móvel de fluido, mas do volume de controle C
 :
 




 

 






 )
(
)
(
)
(
0
lim
t
C
t
C
t
t
C
t
d
t
t
d
d





23. O segundo termo representa a quantidade da grandeza N que deixou o
volume de controle através da superfície S2 por unidade de tempo.
Portanto, é o fluxo da grandeza N para fora do volume de controle
através de S2:
dS
n
t
d
S
r
t
2
0
.
lim
2
2 




 








24. O terceiro termo representa a quantidade da grandeza N que entrou no
volume de controle através da superfície S1 por unidade de tempo.
Portanto, é o fluxo da grandeza N para dentro do volume de controle
através de S1:
dS
n
t
d
S
r
t
1
0
.
lim
1
1 




 








O sinal negativo se deve ao fato de que o sentido da velocidade relativa
sobre a superfície S1 aponta para dentro do volume, enquanto 1
n

aponta
para fora, portanto o produto escalar será negativo.

25. Como a soma das superfícies S1 e S2 é a própria superfície de controle
do fluido:
dS
n
d
t
dt
dN
t
SC
r
t
C


 



 )
(
)
(
.





Se o volume de controle for estacionário a velocidade relativa entre
fluido e volume de controle será a própria velocidade absoluta,
resultando:
dS
n
d
t
dt
dN
SC
C


 






.




26. 3)Equação da Continuidade ou Conservação da Massa
Se aplicarmos o Teorema do Transporte de Reynolds para uma massa
móvel e fixa de fluido em movimento ( o que chamamos de sistema) de
modo que N=m e 1

 , teremos, por definição:
0

dt
dm
0
. 


 



dS
n
d
t SC
C






27. Esta última equação é a chamada Equação da Continuidade ou Equação
da Conservação da Massa.
Essa equação admite uma série de simplificações:

28. a)Regime Permanente: em cada volume elementar 
d a massa
específica permanece constante ao longo do tempo. Isso significa que:
0

 


C
d
t

A equação da continuidade se resume a:
0
. 
 dS
n
SC





29. Como temos uma superfície lateral impermeável, só teremos fluxos de
massa através das superfícies S1 e S2:
0
.
.
2
1



 dS
n
dS
n
S
S








Na superfície S2 o produto escalar 


.
n é positivo e na superfície S1 é
negativo. Assim:
0
1
2 
m
m 

Se a massa específica for uniforme nas superfícies S1 e S2, podemos
escrever Q
m 

 e teremos:
1
1
2
2 Q
Q 
 

30. b)Escoamento Incompressível
Nesse caso a massa específica é constante no tempo e uniforme no
espaço, e a equação da continuidade resulta:
0
. 
 dS
n
SC



Para o volume de controle ilustrado na última figura:
0
.
.
2
1



 dS
n
dS
n
S
S







31. Resultando:
1
2 Q
Q 
Ou:
1
1
2
2 S
V
S
V 

32. Exercício: Na seção (1), temos um perfil de velocidades do tipo:
 
7
/
1
max 1 







R
r
V
r

Onde Vmax = 0,122 m/s. O conduto é circular, com D1=0,5m e D2=0,1m.
Calcule a velocidade média na seção (2) considerando escoamento
incompressível.

33. Solução:
Para um escoamento incompressível da continuidade temos que:
2
2
1
1
2
1 S
V
S
V
Q
Q 


De exercício anterior,

 max
1
60
49
V
V m/s
100
,
0
122
,
0
60
49
1 


V

34. Da equação da continuidade:
2
2
1
1
2
2
2
2
2
1
1
4
4









D
D
V
V
D
V
D
V


Assim:









2
2
1
,
0
5
,
0
100
,
0
V m/s
5
,
2
2 
V

35. Exercício: Um foguete queima  kg/s de combustível. Se mo é a massa
inicial de combustível do foguete, S é a área do bocal de saída dos gases,
 é a densidade dos gases no bocal e V é a velocidade relativa de saída
dos gases em relação ao foguete, obtenha uma expressão para V.

36. Solução: da continuidade, 0
.
)
(
)
(



 



dS
n
d
t t
SC
r
t
C




 .
A primeira integral representa a massa do C
 .Assim:
0
.
)
(




  dS
n
t
m
t
SC
r
C 



Mas a massa do volume de controle é dada por:
t
m
m o
C 




37. Assim:
0
0
.
)
(








  VS
dS
n
t
m
t
SC
r
C 





Que resulta:
S
V




38. Bibliografia:
Bistafa, S.R., “Mecânica dos Fluidos, Noções e Aplicações”, 2ª Edição,
Ed. Blucher, 2016.
White, F.M., “Mecânica dos Fluidos”, 5º edição, Ed. McGraw Hill,
2010.
Potter, M.C.; Wiggert, D.C., “Mecânica dos Fluidos”, Ed. Thomson
Learning, 2004.