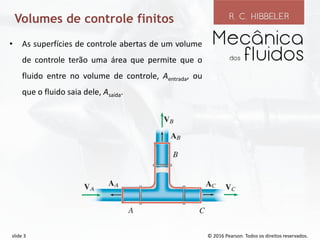
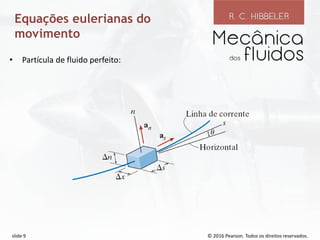
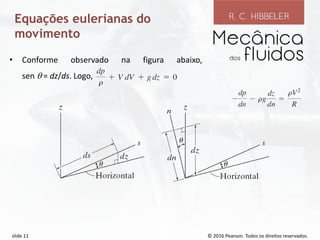
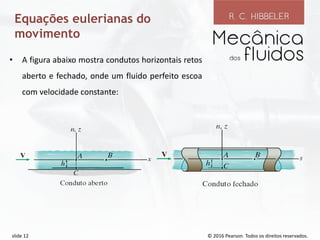
O documento discute conceitos fundamentais de dinâmica de fluidos como volumes de controle, teorema de transporte de Reynolds, conservação da massa e equações de Bernoulli. Ele explica como definir volumes de controle finitos e especificar vazões de entrada e saída, e como o teorema de transporte de Reynolds relaciona a taxa de variação de propriedades dentro de um volume de controle.

1. Conservação de massa e
Energia
© 2016 Pearson. Todos os direitos reservados.
slide 1

2. © 2016 Pearson. Todos os direitos reservados.
slide 2
Volumes de controle finitos
• Podemos considerar volumes de controle que
possuem um tamanho finito, como aquele
mostrado na figura abaixo:

3. © 2016 Pearson. Todos os direitos reservados.
slide 3
Volumes de controle finitos
• As superfícies de controle abertas de um volume
de controle terão uma área que permite que o
fluido entre no volume de controle, Aentrada, ou
que o fluido saia dele, Asaída.

4. © 2016 Pearson. Todos os direitos reservados.
slide 4
Volumes de controle finitos
• Como a normal para fora para cada área da superfície de controle é positiva,
então o escoamento que entra em uma superfície de controle será negativo, e o
escoamento que sai de uma superfície de controle será positivo.
• Em alguns problemas, será vantajoso selecionar um volume de controle em
movimento a fim de observar o escoamento em regime permanente, e assim
simplificar a análise.
• Ao usar um volume de controle, também teremos
de especificar a velocidade tanto do escoamento
que entra quanto do que sai da superfície de
controle.

5. © 2016 Pearson. Todos os direitos reservados.
slide 5
O teorema de transporte de
Reynolds
• O teorema de transporte de Reynolds relaciona a taxa de variação no tempo
de qualquer propriedade extensiva N de um sistema de partículas de fluido,
definida a partir de uma descrição lagrangeana, às variações da mesma
propriedade do ponto de vista do volume de controle, ou seja, conforme
definida a partir de uma descrição euleriana.

6. © 2016 Pearson. Todos os direitos reservados.
slide 6
O teorema de transporte de
Reynolds
• O primeiro termo no lado direito é a variação local, pois representa a taxa de
variação no tempo na propriedade intensiva dentro do volume de controle.
• O segundo termo à direita é a variação convectiva, pois representa o
escoamento resultante da propriedade intensiva através das superfícies de
controle.
• Ao aplicar o teorema de transporte de Reynolds, é necessário primeiro
especificar o volume de controle que contém uma parte selecionada do sistema
de fluido.

7. © 2016 Pearson. Todos os direitos reservados.
slide 7
Vazão volumétrica, vazão
mássica e velocidade média
• Em muitos problemas envolvendo o escoamento unidimensional, a velocidade
média V poderá ser usada. Se o escoamento for conhecido, então ele pode ser
determinado a partir de V = Q/A.
• A vazão mássica é determinada por ou, para um fluido
incompressível tendo uma velocidade média,
• A taxa na qual um volume de fluido escoa por
uma seção transversal A é chamada de vazão
volumétrica, ou simplesmente vazão ou
descarga.

8. © 2016 Pearson. Todos os direitos reservados.
slide 8
Conservação da massa
• Portanto, a conservação de massa requer que
• Essa equação normalmente é chamada de equação da continuidade.
• A conservação da massa declara que, dentro de
uma região, fora de qualquer processo nuclear, a
matéria não pode ser criada nem destruída.

9. © 2016 Pearson. Todos os direitos reservados.
slide 9
Equações eulerianas do
movimento
• Partícula de fluido perfeito:

10. © 2016 Pearson. Todos os direitos reservados.
slide 10
Equações eulerianas do
movimento
• Diagrama de corpo livre:

11. © 2016 Pearson. Todos os direitos reservados.
slide 11
Equações eulerianas do
movimento
• Conforme observado na figura abaixo,
sen q = dz/ds. Logo,

12. © 2016 Pearson. Todos os direitos reservados.
slide 12
Equações eulerianas do
movimento
• A figura abaixo mostra condutos horizontais retos
aberto e fechado, onde um fluido perfeito escoa
com velocidade constante:

13. © 2016 Pearson. Todos os direitos reservados.
slide 13
A equação de Bernoulli
• A equação acima é conhecida como equação de Bernoulli.
• Quando ela é aplicada entre dois pontos quaisquer, 1 e 2, localizados na mesma
linha de corrente, ela pode ser escrita na forma
escoamento em regime permanente,
fluido perfeito, mesma linha de corrente